Introduction

Multi spin-echo (MSE) sequences have been suggested for T₂ mapping due to shorter scan times compared to single spin-echo protocols. MSE employs a train of refocusing pulses after a single excitation RF pulse. The disadvantage of MSE sequences is that strong signal contamination arising from stimulated echo pathways lead to erroneous T₂ estimation when applying the standard mono-exponential model. Recent work demonstrated that further improvements can be achieved when using echo modulation curves (EMC), which can be pre-computed given the sequence timings and RF pulses characteristics to account for all echo pathways¹. Previous work showed that simultaneous voxel-wise B₁+ estimation with this method is possible but the estimated B₁+ values display a bimodal distribution with the main peak coinciding with the true value^2,3. In this work, we seek to exploit the expected spatial smoothness of the B₁+ field to iteratively improve B₁+ estimation using the Fusion Bootstrap Moves Solver (FBMS)^4,5. We investigate the use of FBMS to improve B₁+ accuracy in the brain and establish spatial homogeneity metrics to evaluate the effect of optimized FBMS regularization parameters compared to the non-regularized EMC method.

Methodology

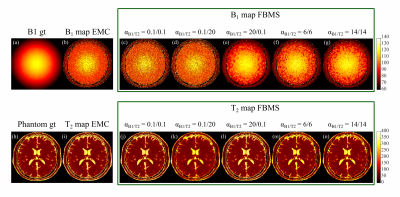
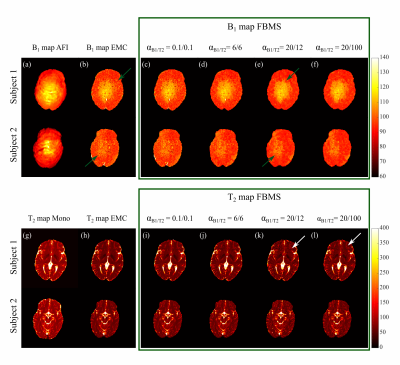
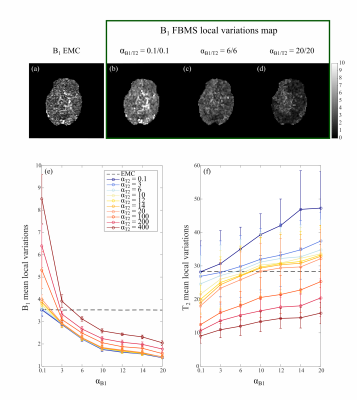
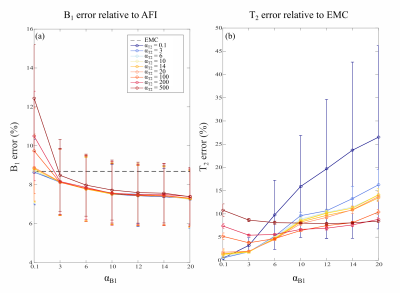
A numerical brain phantom was generated considering three tissue types: cerebrospinal fluid (CSF), white matter (WM) and grey matter (GM), with distinct T₂ and proton density values at 3T³. Simulation of the MSE signal and computation of the EMC dictionary was implemented using the Extended Phase Graph (EPG) formalism⁶, considering a fixed T₁ = 1000 ms (previously reported here¹), a T₂ range of 20:5:400 and 400:100:2000 ms and a B₁+ range of 60:2:140%^2,3. B₁+ and T₂ mapping were obtained using signal matching to the pre-computed EMC dictionary and the proposed FBMS method^4,5. FBMS was implemented with Matlab 2015b (Mathworks, USA). The FBMS algorithm starts by using the B₁+ and T₂ EMC estimated maps as initialization for the iterative model. Then, it applies a binary graph-cut solver, allowing to combine a previous and an updated B₁+/T₂ estimated proposal until it better fits the acquired T₂-weighted signal. Spatial regularization of the B₁+/T₂ maps was controlled using the factors ɑ_B1 and ɑ_T2, respectively. Since FBMS improves B₁+ estimation by taking into account the surrounding pixels’ estimates, a spatial smoothness metric was established by calculating the local standard deviation within a 3x3 pixel neighborhood. In-vivo brain data was acquired in a cohort of three healthy subjects using a Philips Achieva 3T scanner. MSE sequence was implemented with: TR = 4s, ETL = 32 (dTE = 10ms), spatial resolution 1.6×1.6×4.0mm3 and FOV 250×250mm2. B₁+ maps were also acquired with the Actual Flip Angle (AFI)⁷ method (3.9mm isotropic resolution, FOV = 250×250×250mm3, TE/TR = 0.78/25ms, TR extension 100ms). B₁+ estimation with FBMS and EMC was analyzed considering both accuracy (error relative to ground truth or in-vivo reference) and spatial homogeneity metric (standard deviation within pixel-neighborhood). For in-vivo analysis, B₁+ FBMS estimation was compared to B₁+ AFI method (considered as gold standard) and the T₂ FBMS was compared to the original EMC estimate (here considered as reference), since mono-exponential fitting is known to be erroneous¹. Optimization of the regularization factors and their impact on B₁+ smoothness (novel local variations metric) and accuracy were here investigated in a larger cohort, compared to previous work³.

Results

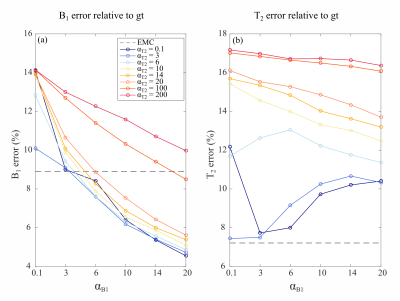
Numerical phantom results are shown in Figure 1. B₁+ accuracy was improved with FBMS compared to EMC (Figure 2 a). However, T₂ accuracy worsens (Figure 2 b) with the use of FBMS regularization due to adding of textured noise and enforced T₂ smoothness where it should not be expected (Figure 1). Example of in-vivo B₁+ and T₂ brain maps computed with EMC and FBMS are shown in Figure 3. B₁+ and T₂ local variations metric (smoothness) and corresponding maps are summarized in Figure 4. B₁+ spatial smoothness was improved with FBMS, as demonstrated by the decrease in local neighborhood variations around the initial pixel-wise estimation (Figure 4 e). Similarly to simulations, overall B₁+ accuracy with FBMS also improved in-vivo (Figure 5 a), proportionally to the increase in ɑ_B1 regularization. A systematic bias when comparing the B₁ FBMS estimation to AFI is present of approximately 7%, however simulation work showed good B₁ FBMS accuracy improvement when compared to true value. Although simulations reported a lower T₂ accuracy with FBMS compared to ground truth, in-vivo results demonstrated that the reduced T₂ accuracy can be kept at acceptable values compared to the initial T₂ EMC estimate, by adjusting the T₂ relative weights (Figure 5 b).

Discussion and Conclusions

B₁+ spatial smoothness and accuracy compared to simulated ground truth and AFI in-vivo was improved with FBMS. As expected, the improvement was proportional to the ɑ_B1 parameter. However, an increase in textured noise can be seen in the T₂ maps when applying FBMS due to enforced smoothness. This can be partially counteracted using the ɑ_T2 parameter albeit with limitations, since T₂ is intrinsically spatially variant depending on tissue-type properties. In summary, FBMS is a promising tool to improve B₁+ accuracy and spatial smoothness, though careful use should be considered to minimize the effects on T₂ estimation.

Acknowledgements

Portuguese Foundation for Science and Technology (FCT - IF/00364/2013, UID/EEA/50009/2019, SFRH/BD/120006/2016), and POR Lisboa 2020 (LISBOA-01-0145-FEDER-029686).