Introduction

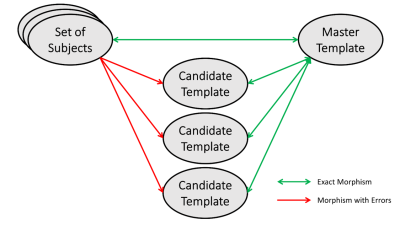
Voxel-wise analyses of brain DTI, fMRI or any other MRI-derived metric, comparing groups or one patient to a group, rely on registration to a brain template to ensure that homologous regions are being compared. The neuroanatomical variability among individuals virtually ensures that one brain can never be exactly mapped onto another.^1-4 Because quality of inter-brain registrations is sensitive to the similarity between them, results of voxel-wise analyses are sensitive to the choice of the template.⁴

Registration errors cause two main difficulties for studying sensitivity to the choice of template: absence of the “ground truth” and comparison of results obtained over different individual templates. In an ideal scenario (Fig 1), subject data is registered to a master template without errors for a voxel-wise analysis to generate the “ground truth”. The same analysis is performed over the various candidate templates. Subsequently, clusters are carried over to the master template without misalignment for comparison with the ground truth. If the clusters match the ground truth, the candidate template may be termed as “good”. Otherwise, it is “bad”. This ideal scenario would allow detailed analysis of the quality of the individual morphisms and development of a criterion with which to screen and filter out aberrant transformations thus converting a “bad” template into a “good”, albeit for a subset of subjects.

In the present study, we develop an “induction” process to manufacture the needed error-free morphisms. We then examine how template selection affects the results of a voxel-wise fractional anisotropy (FA) analysis that seeks to reproduce the well-known decline in white matter integrity with age. We demonstrate that excluding poorly-registered images dramatically increases robustness of the voxel-wise analysis to the choice of template.

METHODS

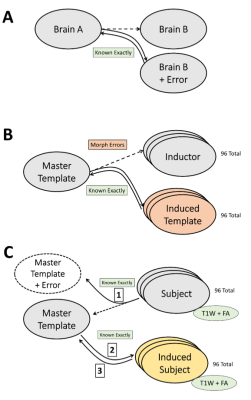
This study was approved by IRB and includes 96 datasets obtained as part of ongoing Einstein Lifespan Study (ELS). Images were reviewed by an experienced neuroradiologist and determined to be free of visible structural abnormalities. Imaging was performed using a 3.0T Philips Achieva TX scanner (Philips Medical Systems, Best, The Netherlands) utilizing its 32-channel head coil with the following protocol. T1W: TR/TE/TI = 9.9/4.6/900 msec, flip angle 8deg, 1mm³ isotropic resolution, 128x116x220 matrix; DTI: TR/TE = 10,000/65msec, 32 diffusion directions, b-value = 800 sec/mm², 2mm³ isotropic resolution, 240x188x70 matrix; and field map to remove EPI distortions in DTI and small distortions in T1W: TR/TE = 20/2.4 msec, delta TE=2.3msec, flip angle 20deg, 4mm³ isotropic resolution, 64x64x50 matrix. DTI data were eddy corrected and registered to T1W. All brain extractions and registrations were visually inspected. All non-linear registrations (morphisms) were performed using ART.² Clusters of voxels where FA was significantly correlated with age were identified by performing voxel-wise t-test with gender as covariate at p=0.005 and retaining clusters of 100 or more contiguous voxels.

We recognize that even with the best available algorithms, morph errors between brains A and B can never be turned off. However, a morphism can transform image A into another image B'. Image B' does not match image B exactly, but transformation between A and B' is exact by construction (Fig. 2A). When we take A to be the master template, we refer to image B' as the “induced template” with image B being the “inductor”. Specifically, we selected the JHU brain as the master template and morphed it onto the 96 T1W images of the ELS as inductors to produce 96 induced templates to be used as candidate templates (Fig. 2B). A similar induction process is used to turn off morph errors between subjects and the master template (Fig. 2C).

All 96 induced subjects were morphed to all 96 induced templates (red arrows in Figure 1). Each of these 9216 morphisms underwent quality filtering based on displacement of anatomical landmarks delineated by the ASEG module of FreeSurfer⁵ as previously reported.⁶ We defined a morphism as “good” if the mean displacement was less than 0.14mm and as “bad” if it was more than 0.15mm. Morphisms in between are discarded (Figure 3). To eliminate sensitivity to sample size introduced by these quality cuts, we selected 30 subjects, 25 good and 25 bad templates such that all subjects are morphed well to all good and poorly to all bad templates.

RESULTS

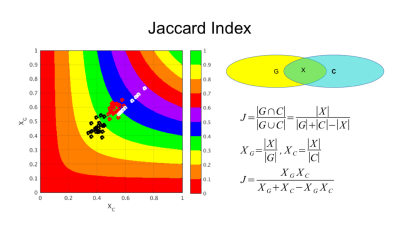
Because the same data were used throughout, the differences between FA clusters are not random but due to registration errors (red arrows in Figure 1). Each of the 50 sets of clusters was compared to the gold standard set using the Jaccard index (Figure 4) demonstrating marked improvement when registration quality filtering is applied. Jaccard index between shifted and unshifted gold standard clusters shows that “good” morphisms produce as good a match as a single diagonal 1mm voxel shift.

CONCLUSION.

Clusters in voxel-wise analyses are sensitive to registration errors which makes them sensitive to the choice of template. Filtering out poorly morphed images dramatically reduces this sensitivity, making cluster analysis more template independent. To eliminate spurious clusters such filtering should be performed even if the template is study-specific. Filtering is especially important when the choice of the template is dictated by some other considerations such as the individual subject T1W image in subject-based analysis.⁴

Acknowledgements

Support for this research was provided in part by the National Institute on Aging, grant 5P01AG003949-34.