1620

Highly Accelerated Time-Encoded Dynamic ASL Angiography

Sophie Schauman¹, Joseph G. Woods^1,2, Mark Chiew¹, and Thomas W. Okell¹
¹Wellcome Centre for Integrative Neuroimaging, NDCN, University of Oxford, Oxford, United Kingdom, ²Department of Radiology, University of California San Diego, La Jolla, CA, United States

Synopsis

Time-encoded (TEnc) dynamic ASL angiography is a method that provides high SNR, dynamic information about the blood supply to the brain. However, as is commonly the case with all ASL-based methods, multiple repeat encodings are required to fully sample the information required to decode the dynamic angiographic data. Here we apply spatial sparsity and temporal smoothness constraints to reconstruct highly under-sampled TEnc data, and demonstrate that high fidelity, high resolution ASL angiography can be performed in a fraction of the time it takes using conventional methods.

Introduction

Arterial spin labelling (ASL) is a non-invasive method for imaging blood flow in the brain. Although typically used for perfusion imaging, it can also be used to create dynamic angiograms by rapid imaging whilst the labelled bolus is still within the arteries.
There are two main approaches to acquiring the temporal information of the bolus’ passage through the arterial tree. The simplest method is to acquire continuously after each labelling (tag or control) block for the desired readout duration and split up the data into a number of frames. This approach requires small flip angles to prevent signal attenuation from each RF pulse during the readout. The other approach is to use time-encoding (TEnc), where the labelling is modulated to carry temporal information¹. In TEnc, the signal is acquired during a shorter readout period and larger flip angles can therefore be used to achieve a higher SNR, especially when combined with a variable flip-angle scheme². This SNR increase was demonstrated to produce improved image quality compared to sequentially acquired angiograms even when undersampled to match scan time².
Typically, multiple repeats of each labelling condition are acquired to fully sample each frame. Here we propose an accelerated approach that can reconstruct under-sampled TEnc dynamic ASL data in a compressed sensing framework, leveraging both the spatial sparsity and temporal smoothness of angiographic data to greatly reduce the required scan time.

Methods

A 2D pseudo-continuous ASL dataset with three readout frames (120 ms each) and three time-encoded blocks (360 ms each) was acquired on a 3T Siemens Verio system, with a 32-channel head-coil. When decoded, this resulted in nine frames with effective post labelling delays of 60 to 1020 ms in steps of 120 ms (Figure 1). Each readout frame was radially fully sampled (552 spokes) for a spatial resolution of 0.63 mm2, FOV = 220 mm2and slice thickness 70 mm. This required 46 repeats of each encoding (total scan time 4.5 min) as 12 spokes (TR = 10ms) were acquired for each frame after each encoding block. A variable flip angle scheme was used as proposed by Woods et al.²
The acquired data were retrospectively undersampled. For R = 12, every 12thspoke was kept starting from the first in the first frame, the fifth in the second readout frame, and the ninth in the third readout frame. The data was similarly undersampled for R = 23 and R = 46 (single shot acquisition). The same undersampling pattern was used for every encoding. This approach ensured different spatial encodings were obtained across frames which can improve the spatial fidelity of the reconstruction when a temporal smoothness constraint is used³.Three methods were then used to reconstruct the data offline:

A naïve re-gridding of the non-cartesian data using the NUFFT⁴.
Non-Cartesian SENSE parallel imaging reconstruction
Compressed sensing reconstruction with sparsity in decoded image space and a temporal smoothness constraint

The cost function was defined as:
$$cost=\frac{1}{2}|Ex-d|_{2}^{2}+\lambda_{1}|x|_{1}+\frac{1}{2}\lambda_{2}|\nabla{}x|^2_{2}$$
where E is the overall encoding operator (including time-encoding, coil sensitivities, and Fourier encoding), x is the angiographic data, d is the measured k-space data, and ∇ is the temporal finite difference operator. The parameters $$$\lambda_1$$$ and $$$\lambda_2$$$ weight the spatial sparsity and temporal smoothness constraints, respectively. This cost function was minimized using FISTA, For the SENSE reconstruction, both $$$\lambda_1$$$ and $$$\lambda_2$$$were set to 0. Coil sensitivity profiles were estimated from the data averaged across readout frames and time-encodings using the adaptive combine approach^6.

Results

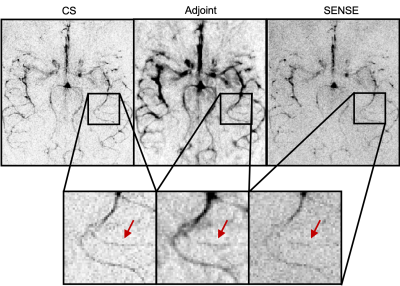
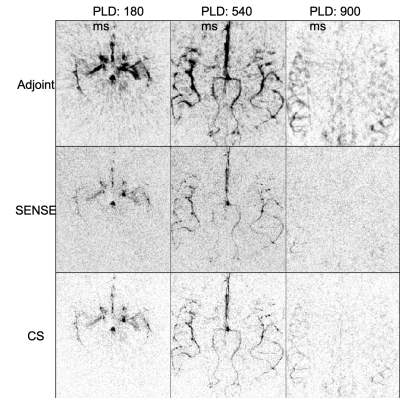
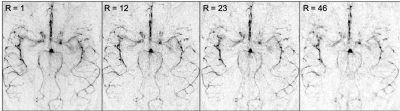
Figure 2 shows a comparison between the different reconstruction methods at acceleration factor R = 12. SENSE reconstructions are sharper than the simple regridding (adjoint), but have taken an SNR penalty compared with the blurry regridded reconstruction. CS, on the other hand retained both contrast and sharpness. Figure 3 shows that temporal dynamics are preserved despite the smooth temporal constraint in the CS reconstruction framework. Also, the distal vessels in the late frames are both sharper than in the regridding reconstruction and have higher SNR than the SENSE reconstruction. Figure 4 shows how the image changes when the undersampling factor is pushed to a single shot acquisition approach. Although the finer details are lost at very high undersampling factors, the CS reconstruction method robustly reconstructs all the main arteries and showcases the range of image qualities available depending on how much scan time can be used.

Discussion

The constrained reconstruction framework used here for high resolution TEnc dynamic ASL angiography is capable of producing high fidelity angiograms in a fraction of the time normally needed for a fully-sampled acquisition. Conventional gridding reconstructions resulted in apparent blurring and clear residual aliasing at higher acceleration factors, whereas the non-Cartesian SENSE reconstructions resulted in noise amplification and loss of vessel contrast. The sparse reconstruction, exploiting spatial sparsity and temporal smoothness, however, showed excellent image quality up to acceleration factors of R=23, turning 4.5 minutes of data acquisition into 12 seconds. The temporal smoothness, in particular, allows for sharing of sampling information across frames, significantly enhancing reconstruction performance.
Future directions will include 3D angiography, allowing for even higher acceleration factors, and combining TEnc schemes with vessel-encoding7or perfusion imaging8in a constrained reconstruction framework.

Acknowledgements

This work was supported by funding from the Engineering and Physical Sciences Research Council (EPSRC) and Medical Research Council (MRC) [grant numberEP/L016052/1].

The Wellcome Centre for Integrative Neuroimaging is supported by core funding from the Wellcome Trust (203139/Z/16/Z). MC (RF201617\16\23) and TO (RF/132) are supported by the Royal Academy of Engineering

References

1.Suzuki Y, Teeuwisse WM, Schmid S, Helle M, Cauteren M Van, Osch MJP Van. Improving 4D pCASL angiography by combining Hadamard time-encoding with Look-Locker readout. In: Proc. Intl. Soc. Mag. Reson. Med. 22. ; 2014. p. 6460.2. Woods JG, Schauman SS, Chiew M, Chappell MA, Okell TW. Optimization of time-encoded pseudo-continuous ASL angiography with a variable flip-angle scheme. In: Proceedings 27th Scientific Meeting, ISMRM. Montreal, Canada; 20193.Schauman SS, Chiew M, Okell TW. Highly accelerated vessel‐selective arterial spin labeling angiography using sparsity and smoothness constraints. Magn Reson Med 2019:mrm.27979 doi: 10.1002/mrm.27979.4. Fessler JA, Sutton BP. Nonuniform fast Fourier transforms using min-max interpolation. IEEE Transactions on Signal Processing 2003;51:560–574 doi: 10.1109/TSP.2002.807005.5. Pruessmann, Klaas P, M Weiger, P Börnert, and P Boesiger. “Advances in Sensitivity Encoding with Arbitrary K-Space Trajectories.” Magnetic Resonance in Medicine46, no. 4, 2001: 638–516. Walsh, D O, A F Gmitro, and M W Marcellin. “Adaptive Reconstruction of Phased Array MR Imagery.” Magnetic Resonance in Medicine43, no. 5, 2000: 682–907.Wong, Eric C. “Vessel-Encoded Arterial Spin-Labeling Using Pseudocontinuous Tagging.” Magnetic Resonance in Medicine 58, no. 6, 2007: 1086–91 8. Okell, Thomas W. “Combined Angiography and Perfusion Using Radial Imaging and Arterial Spin Labeling.” Magnetic Resonance in Medicine 81, no. 1, 2019: 182–94

Figures

Schematic diagram of time-encoding scheme and associated sampling patterns for various under-sampling factors. The 3 time-encoding blocks and 3 readout frames combine to form 9 total effective post-labelling delays.

Figure 2 – Reconstructions at acceleration factor 12 using the sparse (CS), gridding (Adjoint), and SENSE methods. Insets highlight the small subtle vessel features that are well captured in the CS reconstruction, but either missing or only partially captured in the SENSE and gridding reconstructions.

Figure 3 - Comparison of dynamics at an early, mid and late PLDs, for the gridding (Adjoint), SENSE and sparse (CS) reconstructions (R=12). Blurring and residual aliasing can be seen in the Adjoint reconstruction, whereas the SENSE images appear noisy and lacking vessel contrast. The CS reconstructions show significantly improved vessel delineation, particularly at the late PLD.

Figure 4 - Temporal mean of the sparse reconstruction at varying acceleration factors, ranging from fully sampled (R=1) to single-shot (R=46). At R=12 and R=23, considerable detail and image fidelity are preserved, while requiring significantly shorter acquisition times.

Proc. Intl. Soc. Mag. Reson. Med. 28 (2020)

1620