1425
Impact of Scanner Heterogeneity on a Multi-Center Trial1Imaging Institute, The Cleveland Clinic, Cleveland, OH, United States, 2Quantitative Health Sciences, The Cleveland Clinic, Cleveland, OH, United States, 3Lerner Research Institute, The Cleveland Clinic, Cleveland, OH, United States, 4Neurological Institute, The Cleveland Clinic, Cleveland, OH, United States
Synopsis
In a clinical trial, it may be necessary to incorporate multiple centers to get a sufficiently large sample size. Trials that use imaging may suffer from heterogeneity among centers in terms of scanner platform. In the SPRINT-MS trial, diffusion tensor imaging (DTI) measures indicated a larger treatment effect than brain parenchymal fraction (BPF). However, the effect measured by DTI was not statistically significant. In this study, we examine the hypothesis that heterogeneity in scanner type contributed to variance in DTI measures, reducing the statistical power of the measurement.
Introduction
In a clinical trial, it may be necessary to incorporate multiple centers to get a sufficiently large sample size. Trials that use imaging may suffer from heterogeneity among centers in terms of scanner platform. In the SPRINT-MS trial, diffusion tensor imaging (DTI) measures indicated a larger treatment effect than brain parenchymal fraction (BPF). However, the effect measured by DTI was not statistically significant1. In this study, we examine the hypothesis that heterogeneity in scanner type contributed to variance in DTI measures, reducing the statistical power of the measurement.Methods
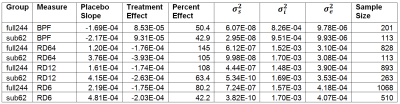
255 patients with secondary or primary progressive multiple sclerosis underwent randomization in a double-blind placebo-controlled longitudinal trial of Ibudilast2. Of these, 244 completed at least two of the five time points (baseline, 24, 48, 72 and 96 weeks), and a subset of 62 was scanned at all five time points on the same make and model of scanner (Siemens Trio). Statistical power depends on the treatment effect, variance and number of subjects. In a longitudinal trial, the variance has several components: variance of slope ($$$\sigma_s^2$$$) and of intercept ($$$\sigma_i^2$$$) among regression lines for each subject and variance around the overall linear trend ($$$\sigma_e^2$$$). If heterogeneity among scanners contributes substantially to variances, a statistical power estimate based on values measured among the subset of 62 patients (sub62) might be comparable to or better than among the full dataset (full244) despite the smaller number of subjects. BPF was determined from the ratio of the brain tissue volume to the outer contour volume3. The DTI measure of interest was radial diffusivity (RD) in corticospinal tracts, measured using high angular resolution diffusion imaging (HARDI) (64 b=700 sec/mm2, 8 b=0 volumes, 2.5mm isotropic voxels)4 and probabilistic tractograpy5. We also examined the impact of using fewer gradient directions (12 and 6) to determine if including sites without access to a HARDI acquisition might be beneficial. Sample size estimates were calculated in R6 using a linear mixed effects model7.Results
Table 1 summarizes the treatment effect, components of variance and the sample size estimate for the full244 and sub62 datasets. For each measure, sample size estimates are smaller when using data from the sub62 dataset than when using the full244 dataset. The statistically significant result for BPF in the overall study is reflected in the fact that the sample size estimate derived from the full244 dataset (201) is less than the total number of subjects examined (244). The sample size estimate for BPF derived from the sub62 dataset is substantially smaller (113). The sample size estimate derived from the sub62 dataset for RD, calculated using all 64 gradient directions, has a similarly small sample size (113). The reduction in sample size estimates associated with using the sub62 instead of the full244 dataset is largely due to a reduction in variance of slope. When RD is recalculated using 12 gradient directions instead of 64 among the sub62 dataset, the sample size estimate is (263) slightly larger than the total number of subjects examined.Discussion
The reduction in sample size estimates associated with using the sub62 dataset instead of the full244 dataset reflects a substantial increase in statistical power associated with reducing scanner heterogeneity. The dominant role played by variance in slope might derive from differences among scanners in sensitivity to changes or instability over time. An extreme example of instability is a scanner upgrade, which affected 29 subjects’ data. Another contribution to variance is missing time points, which affected 54 subjects’ data. The results suggest that, if possible, a longitudinal study should constrain recruitment to sites with the same type of scanner and limit the enrollment and follow-up period to a time short enough to avoid scanner upgrades. As this idealized situation is not always possible, effort to calibrate measurements across scanner types may be beneficial. Framing the effect of calibration in terms of statistical power and sample size estimation provides a practical approach for evaluating the value of such effort.Acknowledgements
This work was supported by NeuroNext (https://neuronext.org/), NIH U01NS082329, NMSS RG 4778 and MedicinovaReferences
1. Fox, R. J., Coffey, C. S., Conwit, R., Cudkowicz, M. E., Gleason, T., Goodman, A., Klawiter, E. C., Matsuda, K., McGovern, M., Naismith, R. T., Ashokkumar, A., Barnes, J., Ecklund, D., Klingner, E., Koepp, M., Long, J. D., Natarajan, S., Thornell, B., Yankey, J., Bermel, R. A., Debbins, J. P., Huang, X., Jagodnik, P., Lowe, M. J., Nakamura, K., Narayanan, S., Sakaie, K. E., Thoomukuntla, B., Zhou, X., Krieger, S., Alvarez, E., Apperson, M., Bashir, K., Cohen, B. A., Coyle, P. K., Delgado, S., Dewitt, L. D., Flores, A., Giesser, B. S., Goldman, M. D., Jubelt, B., Lava, N., Lynch, S. G., Moses, H., Ontaneda, D., Perumal, J. S., Racke, M., Repovic, P., Riley, C. S., Severson, C., Shinnar, S., Suski, V., Weinstock-Guttman, B., Yadav, V., Zabeti, A. & Investigators, N. S.-M. T. Phase 2 Trial of Ibudilast in Progressive Multiple Sclerosis. N Engl J Med 2018; 379(9):846-855.
2. Fox, R. J., Coffey, C. S., Cudkowicz, M. E., Gleason, T., Goodman, A., Klawiter, E. C., Matsuda, K., McGovern, M., Conwit, R., Naismith, R., Ashokkumar, A., Bermel, R., Ecklund, D., Koepp, M., Long, J., Natarajan, S., Ramachandran, S., Skaramagas, T., Thornell, B., Yankey, J., Agius, M., Bashir, K., Cohen, B., Coyle, P., Delgado, S., Dewitt, D., Flores, A., Giesser, B., Goldman, M., Jubelt, B., Lava, N., Lynch, S., Miravalle, A., Moses, H., Ontaneda, D., Perumal, J., Racke, M., Repovic, P., Riley, C., Severson, C., Shinnar, S., Suski, V., Weinstock-Gutman, B., Yadav, V. & Zabeti, A. Design, rationale, and baseline characteristics of the randomized double-blind phase II clinical trial of ibudilast in progressive multiple sclerosis. Contemp Clin Trials 2016; 50(166-177.
3. Fisher, E., Jr., R. M. C., Tkach, J. A., Masaryk, T. J. & Cornhill, J. F. in Medical Imaging 1997 Vol. 3034 (SPIE, 1997).
4. Zhou, X., Sakaie, K. E., Debbins, J. P., Kirsch, J. E., Tatsuoka, C., Fox, R. J. & Lowe, M. J. Quantitative quality assurance in a multicenter HARDI clinical trial at 3T. Magn Reson Imaging 2017; 35(81-90.
5. Lowe, M. J., Beall, E. B., Sakaie, K. E., Koenig, K. A., Stone, L., Marrie, R. A. & Phillips, M. D. Resting state sensorimotor functional connectivity in multiple sclerosis inversely correlates with transcallosal motor pathway transverse diffusivity. Hum Brain Mapp 2008; 29(7):818-827.
6. R Core Development Team. R: A language and environment for statistical computing (R Foundation for Statistical Computing, Vienna, Austria, 2013).
7. Bates, D., Machler, M., Bolker, B. M. & Walker, S. C. Fitting Linear Mixed-Effects Models Using lme4. J Stat Softw 2015; 67(1):1-48.
Figures