Introduction

Axonal injury is a debilitating effect of multiple sclerosis (MS) and a key contributor to physical disability in patients. An accurate and precise biomarker linking in vivo imaging to pathological axonal characterization could improve the clinical study and treatment of MS. One such candidate is a recently developed diffusion MRI method – namely, the spherical mean technique (SMT)¹ – which has shown to be sensitive to various lesion types in MS through voxel-wise mapping of apparent axonal volume fraction^2,3. However, the accuracy and precision of SMT in probing axonal information have not been comprehensively investigated, hindering the application of SMT in MS. To assist implementation and interpretation of clinical MS imaging, we first used previously published SMT results of MS patients to optimize an SMT acquisition protocol for practical MS imaging, and then used computer simulations to determine the accuracy and precision of SMT in providing axonal information under different pathological conditions that may occur in MS lesions.

Methods

Optimization: To optimize precision for better diagnostic specificity, we use a Cramér-Rao Lower Bound (CRLB) approach to minimize the variance of SMT-derived apparent volume fraction (v_ax) with Rician noise (SNR = 20). We limit signals to a total of 100 acquisitions to match the clinically tractable scan time of the widely-used, optimized NODDI acquisition scheme⁴. Four types of tissues were considered: normal white matter, normal appearing white matter, T2-hyperintense lesions, and chronic black-hole lesions. Ground truth SMT metrics were obtained from MS patient data (N=17), giving D_ax ∈ (1.9, 1.8, 1.7, 1.7) µm²/ms and v_ax ∈ (60.7, 45.0, 36.5, 24.1%), respectively for the above tissues^2,3. The optimization minimizes the maximal v_ax CRLB over all tissues – i.e., the worst-case variance.

Computer simulations: Axon bundles were modeled as a two-compartment system; i.e., packed cylinders with a distribution of axon diameters (AxD’s) with various values of v_ax. Intra- and extra-axonal diffusivities were determined from references^5,6 as 2.25 and 2.0 μm²/ms, respectively. A Finite Difference method⁷ was used to simulate noise-free diffusion MRI signals. Random Rician noise at SNR=20 was added to the signals and then SMT fitting was performed using the code available at (https://ekaden.github.io). The fitting accuracy was evaluated using the absolute differences between the mean fits and the ground truth values, and fitting precision was evaluated using the coefficient of variance (COV), i.e., the standard deviations divided by the mean results. Five simulation studies were performed to investigate performance of SMT under different pathologic conditions (Figure 2 through Figure 5).

Results and Discussion

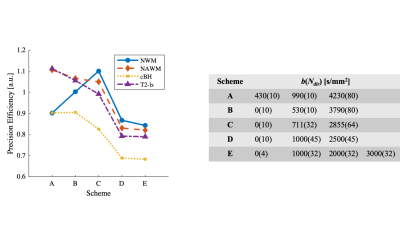
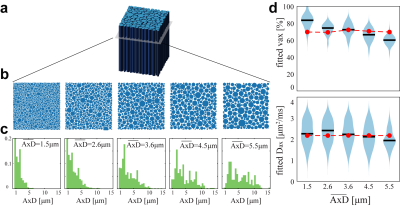
The optimization process yielded an acquisition scheme, described as b-value (number of directions N_dir at the b shell), of {430(10), 990(10), 4230(80) s/mm²}. Figure 1 compares this optimized acquisition scheme to other protocols.

Figure 2 shows the influences of AxD distribution on SMT fitted metrics. For a physiologically relevant range of mean AxDs, SMT provides accurate fits of v_ax from 2.6 to 4.5 μm (differences < 6% of the true values) but overestimates vaxby 18% for small mean AxD (1.5 μm) while underestimating vaxby -13% for large AxD (5.5 μm). Presumably, this is because at small mean AxD, extra-axonal diffusivity at some regions is highly restricted and close to zero. SMT uses zero transverse diffusion as a marker of thin axons, so it could misidentify some extra-axonal space as axonal spaces and hence overestimate v_ax. Similarly, when AxD is very large, some intra-axonal is not zero so that SMT fitting can misidentify parts of these large axons as extra-axonal space. For D_ax fittings, although the accuracy is desirable (differences < 8%), the COV’s are > 70% for all mean AxD values. This is consistent with previous reports of SMT imaging in MS patients that D_ax is not a reliable indicator of MS lesions due to large variance.

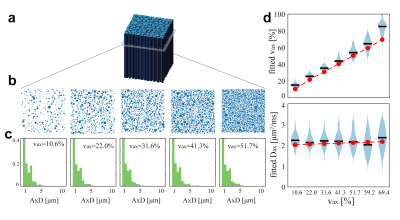
Figure 3 shows the influences of the ground truth vaxon the estimates of vaxand Dax. Despite consistent overestimates of v_ax (~8.8 – 46.7%), the fitted v_ax shows a clear linear correlation with ground truth v_ax (r = 0.97, p<0.01 using Pearson’s correlation). This suggests v_ax can be used a sensitive indicator to axonal contents, which is consistent with previous reports of SMT imaging in MS^2,3.

The influence of free water signal fractions is shown in Figure 4. Neither v_ax or D_ax can be fit with high accuracy or precision. However, v_ax shows a clear dependence on free water fraction (r = 0.92, p<0.01), indicating that even if SMT is a two-compartment model, it still can provide valuable information on axonal content when three compartments are present.

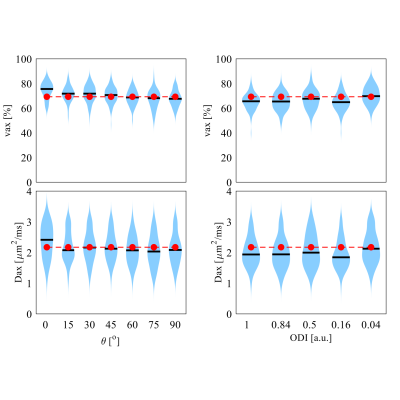
Figure 5 shows that SMT fittings were independent on the crossing angles of two fiber bundles and dispersion of a single fiber bundle. This confirms that SMT is insensitive to the fiber orientations, which is an advantage of SMT in brain imaging.

Conclusion

A biomarker such as axonal volume fraction to link in vivo imaging to axonal injury could improve diagnostics in multiple sclerosis. We report an optimized protocol for v_ax estimation using SMT for MS imaging. We then used computer simulations to comprehensively investigate the accuracy and precision of SMT fitting under different pathological conditions. These results could assist better implementation and interpretation of SMT imaging in MS patients.

Acknowledgements

No acknowledgement found.