Purpose

The long scan time of 3D isotropic MRI (often 5 minutes or longer) has limited the wide clinical adoption despite the apparent advantages. For many clinical sites, shorter 2D sequences are used routinely in brain MRI exams instead. The latest development of deep learning (DL) has demonstrated the feasibility of significant resolution improvement from low resolution acquisitions [1-6]. In this work, we propose a deep learning method to synthesize 3D 1mm isotropic FLAIR images from 2D FLAIR acquisition with 5mm slice thickness. To demonstrate the generalizability, the proposed method is validated on both simulated and real 2D FLAIR datasets.

Methods

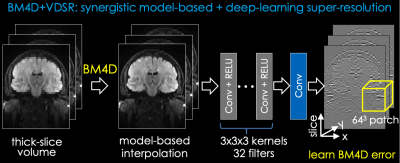
The proposed method is illustrated in Fig. 1 with two sequential steps. All operations in the proposed approach are performed on the magnitude coil-combined images.

(1) BM4D: The 2D thick-slice FLAIR images are first interpolated into an isotropic 3D volume using BM4D [7,8], a model-based method. Define $$$y$$$ as a thick slice in the 2D acquisition and $$$x$$$ the corresponding $$$n$$$ slices from the target 3D isotropic volume. In this work, all 2D FLAIR images were acquired with 5mm slice thickness and 1mm² in-plane resolution, and the target 3D volume was acquired with 1mm³ isotropic resolution (i.e., $$$n=5$$$). The BM4D problem can be formulated as a decoupled optimization problem: $$\hat{x}_i = \mathop{\mathrm{arg\,min}}_x ||Ax-y||_2^2+\alpha ||x-x_{i-1}||_2^2$$
$$x_i = \mathop{\mathrm{arg\,min}}_x ||x-\hat{x}_i ||_2^2 + \lambda\rho (x)$$
Here, $$$A$$$ is approximated as a row of $$$n$$$ “1”s, the summation of $$$n$$$ slices; $$$\alpha$$$ was gradually reduced from 200 to 1 across 25 iterations to optimize RMSE. Optimization results were not sensitive to the choice of $$$\alpha$$$, which was set to 1e-16.

(2) DL: A VDSR network [9] with 20 layers is applied to further enhance the images after BM4D. Residual learning is performed to synthesize the difference between BM4D and the ground truth 3D volume. 3D isotropic FLAIR datasets were used to simulate thick-slice 2D datasets with 5mm slice thickness and create paired 2D/3D datasets. Patched based training with 64$$$\times$$$64$$$\times$$$64 patches extracted from the 3D volume is implemented.

With IRB approval and patient consent, 20 patients were recruited for this study. 3D FLAIR images were collected as part of the routine clinical protocol. 17 datasets were used to create training data for the VDSR network. The remaining 3 datasets were used for testing. The training pairs were flipped in three directions for data augmentation. The proposed model was trained with ADAM optimization, 0.001 learning rate and 20 epochs. Because the proposed network is fully convolutional, the inference was performed on the entire 3D volume instead of patches. To test the generalizability of the proposed method, 10 additional subjects were recruited at another institution. 2D axial FLAIR images with 5mm slice thickness were obtained from the routine protocol at the second institution. Results from different methods were visually and quantitatively compared using the RMSE metric when isotropic 3D volume is available.

Results

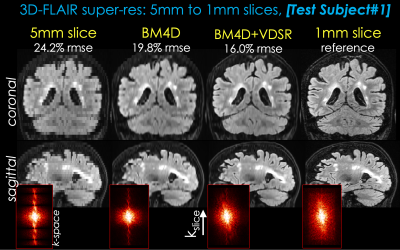
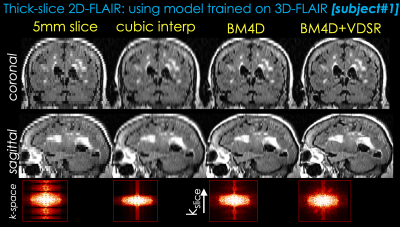
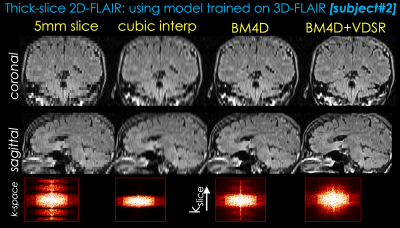
Two representative test datasets from the first institution are shown in Figs. 2 and 3, respectively. The proposed method can achieve significantly better image quality than BM4D alone. Representative results from the second institution are shown in Figs. 4 and 5, respectively. Compared with simple cubic interpolation, BM4D provides better image quality and initialization for VDSR. Combined with VDSR, the proposed approach achieved the best image quality of all the methods compared.

Discussion and Conclusion

In this work, we propose a deep learning approach to synthesize high resolution 3D volumetric images from 2D thick slices. BM4D provides better initialization for the deep learning model than direct cubic interpolation. Though not directly comparable, the k-space images of different reconstructions suggest that the proposed method has recovered more information than BM4D. Furthermore, the proposed method has been validated on real 2D acquisitions from a different institution and protocol, demonstrating good generalizability of the proposed method. While there are still visual differences between the proposed method and real isotropic images, we believe this is a good first step and feasibility test. Future work will focus on reducing the remaining differences and thorough clinical validation.

Acknowledgements

No acknowledgement found.