Introduction

Recently, deep-learning techniques^1-3 have been applied to MRI reconstruction from highly undersampled k-space data, attracting considerable interest due to their promise for improving image quality compared to PICS (parallel imaging and compressed sensing) methods. However, despite improved overall image quality, deep learning-based methods sometimes produce residual image blurring, with some loss of fine detail. The use of structural similarity (SSIM)⁴ as a loss function for network training was recently shown⁵ to produce sharper MR images than L2. And the combination of multi-scale SSIM and L1 outperformed other loss functions in super-resolution, denoising, and deblocking of natural images⁶. Here we explore the use of other variations of SSIM, including contrast-weighted SSIMs, as loss functions for undersampled MRI reconstruction.

Methods

We use a DCI-Net (Densely Connected Iterative Network)³, an unrolled compressed-sensing iterative reconstruction consisting of multiple iterative blocks, each of which includes a data-consistency unit and a convolutional unit for regularization, with dense skip-layer connections among iterations. An example network was chosen with 20 iterations, 12 layers per iteration, 64 3x3 filters per layer, and 8 dense skip-layer connections per iteration.

The SSIM function can be defined as⁴ $$\mathrm{SSIM}(x,y)=l(x,y)^{\alpha}c(x,y)^{\beta}s(x,y)^{\gamma}$$ for two image patches $$$x$$$ and $$$y$$$, where $$$l$$$, $$$c$$$ and $$$s$$$ are the luminance, contrast and structure comparison functions, and $$$\alpha$$$, $$$\beta$$$ and $$$\gamma$$$ are the weights. When $$$\alpha=\beta=\gamma=1$$$, this becomes the conventional unweighted SSIM. The comparison functions are given by $$l(x,y)=\frac{2\mu_x\mu_y+c_1}{\mu_x^2+\mu^2_y+c_1}$$ $$c(x,y)=\frac{2\sigma_x\sigma_y+c_2}{\sigma_x^2+\sigma_y^2+c_2}$$ $$s(x,y)=\frac{\sigma_{xy}+c_3}{\sigma_x+\sigma_y+c_3}$$ where $$$\mu_x$$$ and $$$\mu_y$$$ are the means of $$$x$$$ and $$$y$$$, $$$\sigma_x$$$ and $$$\sigma_y$$$ are the variances, $$$\sigma_{xy}$$$ is the covariance, $$$c_1=(k_1L)^2$$$, $$$c_2=(k_2L)^2$$$, and $$$c_3=c_2/2$$$ with $$$k_1=0.01$$$, $$$k_2=0.03$$$ and $$$L$$$ is the dynamic range. Given a network output image and a fully-sampled reference image, the SSIM is calculated for 11x11 image patches, centered around each pixel of the two images, and the mean of the SSIM over the entire image is used as the loss function. We have used different loss functions for training the network, including L1, the conventional unweighted SSIM⁴, and various weighted SSIM (wSSIM), where $$$\alpha$$$, $$$\beta$$$ and/or $$$\gamma$$$ can deviate from 1. As one example, a contrast-weighted grouping of $$$\alpha=0.3$$$, $$$\beta=1$$$, and $$$\gamma=0.3$$$ was chosen for closer analysis based on preliminary visual assessment of reconstructed images with respect to blurring, noise, and artifacts.

Fully-sampled T1 and T2-weighted fast-spin-echo MRI head datasets were acquired using a variety of 8 to 49-channel head arrays. The data were retrospectively down-sampled with a net undersampling factor of 3.7 and used for training and testing. In total, 3062 slices were collected, of which 1901 were used to train the networks, 151 for validation and 1010 for testing. The test data were acquired at the Mayo Clinic on their compact 3T scanner⁷. Mixtures of uniform and variable-density undersampling were used for training, with variable-density sampling used for testing. Complex coil-combined zero-filled reconstructions from the down-sampled data were used as the input to the network, and the fully sampled k-space data were reconstructed to form reference images.

Reconstructed images were quantitatively compared against image metrics relative to fully-sampled ground truth including normalized mean-squared error (nMSE), peak signal-to-noise ratio (PSNR), SSIM and wSSIM. Here we also compared with Autocalibrating Reconstruction for Cartesian imaging (ARC) – where k-space was regularly undersampled, and with a total-variation (TV) based compressed-sensing method⁸ that employed data-driven iterative soft thresholding.

Results

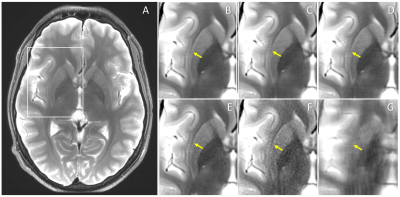
Figures 1 and 2 show representative examples of the test images, comparing the output of the DCI-Net trained using different loss functions. Here wSSIM resulted in better recovery of fine anatomical features than the other loss functions. Table 1 gives a comparison of the quantitative image metrics for different reconstruction methods, calculated from the test data set. The three networks outperformed TV and ARC in all metrics, with the two SSIM losses generating better SSIM metrics than the L1 loss.

Discussion

It has been reported^5,6 that L1 and SSIM loss functions and their variants and combinations can yield better image quality such as improved sharpness compared to conventional L2. In this study, the wSSIM loss function showed better fine-feature recovery than L1, or SSIM, at the cost of somewhat weaker image denoising. The wSSIM loss function encourages similarity in local spatial variance between the network output and the fully-sampled reference image, which appears to improve reconstruction of small anatomical features. The new wSSIM metric merits further investigation, including examining its variants and combination with other loss functions.

Conclusion

The novel weighted SSIM loss function shows promise for reconstructing small anatomical features with better image quality compared to L1 and conventional SSIM loss functions, when applied to reconstructions from highly undersampled k-space data.