INTRODUCTION

Previously, several studies have shown magnitude-based artificial neural network (ANN) on estimating the Myelin Water Fraction (MWF).^1,2 The main benefit of ANN-based MWF was noise-robust mapping as well as fast reconstruction time.^1,2 However, in multi-echo gradient echo (mGRE) sequence, the phase information of the signal need be considered due to the fiber orientation dependency of the frequency offsets.³
Since recent works have shown promising performance with complex-valued network^4,5, this may have a large impact on MWF mapping using ANN. In this sense, we developed a complex-valued neural network for MWF mapping which may reflect the non-linear phase information. Also, numerical simulations and in vivo studies with comparison to 3-pool complex fitting and magnitude-based ANN are performed.

METHODS

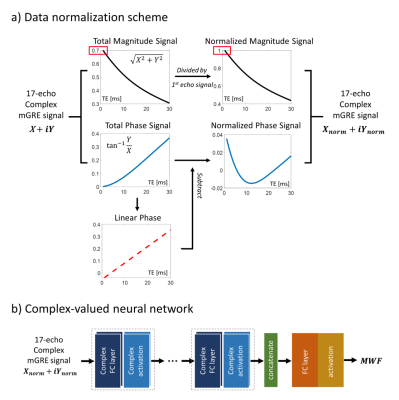
[Complex-valued neural network]
We propose complex-valued ANN for estimating MWF values. Before training the network, data normalization was adopted separately in both magnitude and phase of the signal as described in Fig.1a. The magnitude signal of each voxel was divided by the first echo signal. Phase normalization was done in order to neglect the linear phase term (due to the B0 field). Phase signal was subtracted by the linear phase acquired by line regression of each voxel.
Our proposed complex-ANN is shown in Fig.1b. In specific, complex fully-connected layers were performed with complex-valued activation functions. Since the output of our network is the MWF value (which is magnitude), additional adjusting layers for mimicking the real and imaginary components were adopted. The network takes 17-echo mGRE signal and yields the MWF as the output.
[Training]
Simulation data was used for generating the dataset. 3-pool complex model (composed of myelin water, axonal water, and extracellular water pools) is adopted with plausible ranges.^1,7
$$S(t)=A_{my}e^{-(\frac{1}{T_{2,my}^*}+i2\pi\triangle f_{bg+my})t}+A_{ax}e^{-(\frac{1}{T_{2,ax}^*}+i2\pi\triangle f_{bg+ax})t}+A_{ex}e^{-(\frac{1}{T_{2,ex}^*}+i2\pi\triangle f_{bg+ex})t},MWF = \frac{A_{my}}{A_{my}+A_{ax}+A_{ex}}\times100$$
[Testing]
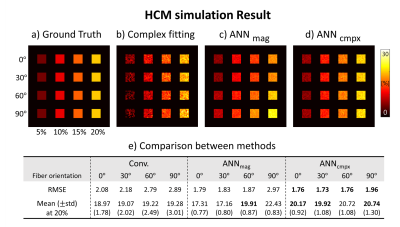
1. Numerical simulation : To compare the performance of proposed complex-ANN in terms of fiber orientations, a hollow cylinder model⁶ was used for the analytic phantom with the following parameters: Isotropic susceptibility = $$$-0.13ppm$$$, anisotropic susceptibility = $$$-0.15ppm$$$, $$$T_{2,my}^*=10ms$$$, $$$T_{2,ax}^*=64ms$$$, $$$T_{2,ex}^*=48ms$$$. Volume fraction for the myelin, axon, and extra-cellular space were 32%, 41%, and 27% respectively, with g-ratio of 0.75. Complex signal evolution was performed with four different orientations and MWF (Fig.3a). Additionally, complex Gaussian noise was added to the simulated signal for SNR of 150.
2. In vivo acquisition: We acquired mGRE data from healthy in-vivo, with following image parameters : 3T MRI, TR = $$$46ms$$$, spatial resolution = $$$1.5mm\times1.5mm\times1.5mm$$$, first TE = $$$2.28ms$$$, echo spacing = $$$1.7ms$$$, last TE = $$$30.8ms$$$.
[Evaluation]
Complex fitting, magnitude-ANN, and proposed complex-ANN were analyzed for the comparison. The complex fitting method is a non-linear least squares algorithm using a three-pool complex model as described in previous studies.^7,8 Magnitude-ANN is described in ref 1.
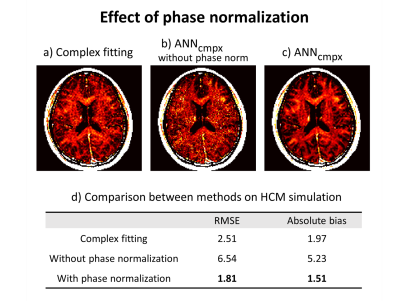
We evaluated the performance of the methods in terms of fiber orientations and noise using analytic phantom and in vivo. To investigate the effect of phase normalization, we compare the results between with and without phase normalization on both numerical simulation and in vivo. Also, an ROI analysis was done in the in vivo data.

RESULTS

Figure 2 shows the effect of fiber orientations and noise on MWF images by proposed complex-ANN and other methods (complex fitting, magnitude-ANN) in simulation. Using the complex fitting was successful for estimating MWF at different fiber orientations (Fig.2b) but fails on robust mapping over the noise. And using the magnitude-ANN was successful for noise-robust mapping (Fig.2c) but fails on different fiber orientations, whereas the complex-ANN (Fig.2d) shows robust results on both fiber orientations and noise.
The effect of phase normalization in the proposed network is shown in Figure 3. In the simulation, the result from the network trained with phase normalized signal provides relatively low RMSE and absolute bias compared to the result from the network trained without phase normalization (Fig.3d). In vivo MWF maps of corresponding methods are shown in Fig.3a-c.
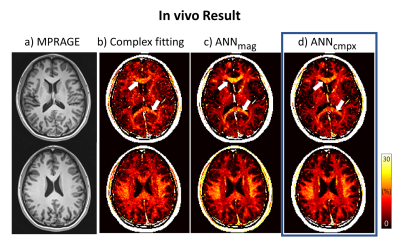
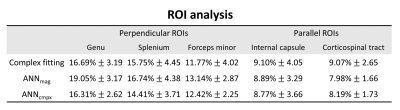
Figure 4 and 5 show the MWF map and ROI analysis on a healthy in vivo case using the three methods. In Figure 4, the result of complex-ANN shows clearer white matter visualization compared to the complex fitting, while provides a relatively low bias in genu and splenium (white arrows) compared to the magnitude-ANN. In the ROI analysis (Fig.5), the results of perpendicular ROIs provide over 2% differences in genu between magnitude-ANN and the other two methods, whereas parallel ROIs show less than 1.1% differences in corticospinal tract.

DISCUSSION AND CONCLUSION

In this study, we investigated the performances of the complex-valued ANN compared to the complex fitting and magnitude-ANN in terms of fiber orientations. Specifically, by numerical simulations, complex-ANN successfully estimated MWF with respect to fiber orientation and noise compared to the other two methods. Also, the complex-ANN produced consistent MWF maps which agreed with the simulation results.
By using complex-ANN, we could take advantages of both fiber orientation robustness of complex fitting and noise robustness of magnitude-ANN. Consequently, our study suggests that complex-valued networks have a potential for better performing on MWF. For further studies, more accurate validations on in vivo will be performed.

Acknowledgements

This work was supported by the National Research Foundation of Korea(NRF) grant funded by the Korea government(MSIT) (NRF-2019R1A2C1090635)