1224
A Paradigm Free Regularization Approach to Recover Brain Activations: Validation on Task fMRI1Athena Project-Team, Inria Sophia Antipolis - Méditerranée, Université Côte d’Azur, Biot, France
Synopsis
In this work we propose and validate a Paradigm-Free fMRI (PFFMRI) algorithm that acts directly on the 4-D fMRI image and recover the underlying brain activations without knowledge on the experimental paradigm. PFFMRI is based on the idea that large image variations should be preserved as they occur during brain activation, but small variations should be smoothed to remove noise. Starting from this, we were able to regularize the fMRI image with an anisotropic regularization, thus recovering the location of the brain activations in space and their timing and duration without knowledge of the experimental paradigm.
Introduction
Resting-state functional MRI (rs-fMRI) provides insight into brain function in the absence of stimuli and allows to map brain activity for subjects whose condition does not allow to perform tasks. This has emphasized the need to recover neural activations from fMRI signals in the absence of an experimental paradigm. To avoid the need for prior information on the timing of the activations, techniques to deconvolve brain activity from the blood-oxygen-level-dependent (BOLD) response have been proposed1-4. In particular, by supposing the brain activates in constant blocks, Farouj et al.4 developed an approach which involves both spatial and temporal regularization (Total Activation, TA). However, it splits the optimization problem into two decoupled spatial and temporal regularization which doubles the number of parameters to set and requires the solver to alternate between the constraints. Starting from the idea that large image variations should be preserved as they occur during brain activation, whereas small variations should be smoothed to remove noise, we previously proposed an alternative paradigm-free algorithm based on partial differential equations (PDEs) named PFFMRI (Paradigm-Free fMRI)4. In this work, we validate PFFMRI on task-fMRI data from 51 subjects using the experimental paradigm as ground truth and compare its performance to TA. We also show that PFFMRI recovers activity that agrees with the general linear model (GLM) without knowledge of the experimental paradigm.Methods
PFFMRI recovers brain activations and smooths small variations by solving the following optimization problem: $$I=argmin_{I}{\parallel I_0-H\star I\parallel}_2^2+\lambda{\parallel\nabla I \parallel}_2^2 \quad (Eq.1)$$ where $$${\parallel I_0-H\star I\parallel}_2^2$$$ is the data fitting term, $$${\parallel\nabla I \parallel}_2^2$$$ is the regularization term, $$$\lambda$$$ is the regularization parameter, I0 and I are the original and regularized image, and H the hemodynamic response function3. Note that the regularization applies on the 4-D image, acting simultaneously in the 3-D space and time and attempts to preserve large image variations occurring in time or space. To solve the problem in Eq.1 we derived a regularization process based on gradient descent computed with PDEs as explained in previous works5,6. To evaluate the performance of PFFMRI, we quantified its ability to recover brain activation during a motor task. It should be noted that, while PFFMRI was designed to be used in the absence of an experimental paradigm, testing it on task-fMRI data provides us with a ground truth to quantitatively assess performance. We used the preprocessed data7 of 51 subjects provided by the Human Connectome Project8 (HCP) that were additionally detrended and normalized. We focused on the motor tasks where subjects were asked to move fingers of their left or right hand. To highlight the ability of PFFMRI to recover brain activations without knowledge of the experimental paradigm, we qualitatively compared brain regions recovered using PFFMRI to those recovered using the GLM implemented in FSL. We also compared the performance of PFFMRI with the deconvolution implemented in TA4. Spherical 3mm-radius ROIs in the motor cortex were defined for each finger starting from the coordinates centers proposed by Roux et al.9 and concatenated to obtain a single ROI for each task. The task ground truth time-courses were constructed as piece-wise constant signals with ones when the subjects were performing the movements and zeros elsewhere. We computed the whole-brain voxel-wise Pearson correlation maps between the time-course of the task and the recovered signals obtained using PFFMRI and TA. For each subject we computed the mean and standard deviation of the correlation inside the ROIs.Results
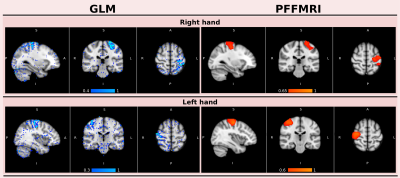
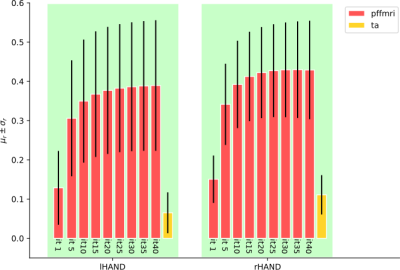
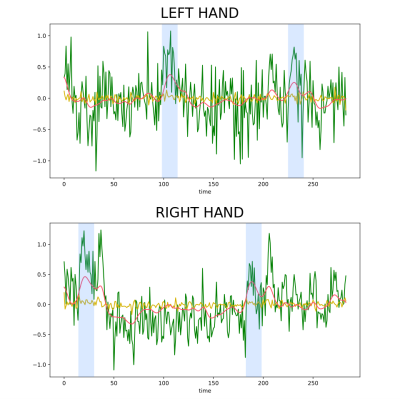
Figure 1 illustrates, for one subject, the correlation maps computed with PFFMRI and the values of the regression coefficients obtained using the GLM. Regions with a high PFFMRI correlation overlap with regions with large GLM regression coefficients. Figure 2 illustrates the mean correlations values estimated for each ROI using PFFMRI and TA. Figure 2 also illustrates the convergence to a stable solution with respect to the number of iterations: the mean correlations values estimated for each ROI across the data sample increase while increasing the number of iterations, until it converges after 25 iterations. Figure 3 illustrates for one subject the recovered signals using PFFMRI and TA averaged in the gray-matter masked ROIs, overlapped to the averaged fMRI data and the experimental paradigm.Discussion
When comparing the regions recovered using the GLM and PFFMRI, we noted overall very good agreement between the methods. It should be emphasized that, while the GLM requires knowledge of the task, PFFMRI does not. These results highlight that PFFMRI can be used to recover brain activity in absence of an experimental paradigm, such as rs-fMRI. When comparing correlation maps obtained for PFFMRI and TA, correlation values obtained with PFFMRI were significantly higher than those obtained with TA suggesting an improved recovery of brain activity.Conclusion
In this paper we validated our approach to recover brain activity from fMRI signals without prior knowledge. Our findings shows that PFFMRI enabled us to solve a unique problem, coupling the space and time dimension and to recover brain activation overlapping the ones obtained with the GLM. Our results also shows higher correlations of the recovered time-courses with the ground truth compared to TA. This opens a new channel for the analyses of rs-fMRI and the recovery of paradigm-free neural activity.Acknowledgements
This work has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation program (ERC Advanced Grant agreement No 694665 : CoBCoM - Computational Brain Connectivity Mapping).
Data were provided [in part] by the Human Connectome Project, WU-MinnConsortium (Principal Investigators: David Van Essen and Kamil Ugurbil;1U54MH091657) funded by the 16 NIH Institutes and Centers that support the NIH Blueprint for Neuroscience Research; and by the McDonnell Center for Systems Neuroscience at Washington University.
References
[1] C. C. Gaudes, N. Petridou, I. L. Dryden, L. Bai, S. T. Francis, and P. A.Gowland, Detection and characterization of single-trial fmri bold responses:Paradigm free mapping, Human brain mapping, vol. 32, no. 9, pp. 1400-1418, 2011.
[2] C. Caballero Gaudes, N. Petridou, S. T. Francis, I. L. Dryden, and P. A.Gowland, Paradigm free mapping with sparse regression automatically detects single-trial functional magnetic resonance imaging blood oxygenation level dependent responses, Human brain mapping, vol. 34, no. 3, pp. 501-518, 2013.
[3] F. I. Karahanoglu, C. Caballero-Gaudes, F. Lazeyras, and D. Van De Ville, Total activation: fmri deconvolution through spatio-temporal regularization, Neuroimage, vol. 73, pp. 121-134, 2013.
[4] Y. Farouj, F. I. Karahanoglu, and D. Van De Ville, Regularized spatiotemporal deconvolution of fmri data using gray-matter constrained total variation, in Biomedical Imaging (ISBI 2017), 2017 IEEE 14th International Symposium on, pp. 472-475, Ieee, 2017.
[5] I. Costantini, S. Deslauriers-Gauthier, and R. Deriche, Novel 4-D algorithm for functional mri image regularization using partial differential equations, in nternational Society for Magnetic Resonance in Medicine (ISMRM) 27th Annual Meeting, 2019.
[6] I. Costantini, S. Deslauriers-Gauthier, and R. Deriche, Deconvolution of fmri data using a paradigm free iterative approach based on partial differential equations, in 2019 Organization for Human Brain Mapping (OHBM) Annual Meeting, 2019.
[7] M. F. Glasser, S. N. Sotiropoulos, J. A. Wilson, T. S. Coalson, B. Fischl,J. L. Andersson, J. Xu, S. Jbabdi, M. Webster, J. R. Polimeni, et al., “The minimal preprocessing pipelines for the human connectome project,”Neuroimage, vol. 80, pp. 105–124, 2013.
[8] D. C. Van Essen, S. M. Smith, D. M. Barch, T. E. Behrens, E. Yacoub,K. Ugurbil, W.-M. H. Consortium, et al., “The wu-minn human connectome project: an overview,”Neuroimage, vol. 80, pp. 62–79, 2013.
[9] F.-E. Roux, I. Djidjeli, and J.-B. Durand, Functional architecture of the somatosensory homunculus detected by electrostimulation, The Journal of physiology, vol. 596, no. 5, pp. 941-956, 2018.
Figures