1153
Using the random permeable barrier model to predict fiber size in histology informed simulated skeletal muscle models1Nanoengineering, University of California, San Diego, La Jolla, CA, United States, 2Orthopaedic Surgery, University of California, San Diego, La Jolla, CA, United States, 3Radiology, University of California, San Diego, La Jolla, CA, United States, 4Bioengineering, University of California, San Diego, La Jolla, CA, United States
Synopsis
There is growing interest in using the Random Permeable Barrier Model (RPBM) to measure muscle microstructure. The goal of this study was to evaluate the accuracy of RPBM in predicting muscle fiber size in histology informed models of healthy and injured skeletal muscle from simulated DTI data. RPBM was found to systematically underestimate fiber size, but accurately predicted surface area to volume ratio (S/V) of the simulated muscle fibers. While the clinical interpretation of S/V ratio is unclear, this indicates that accurate measurement of S/V may serve as a proxy to changes in muscle fiber size and therefore function.
INTRODUCTION
Skeletal muscle is a highly plastic tissue, able to alter its structural and functional properties to match environmental demands. A key plastic feature of muscle microstructure is fiber size, which is directly related to isometric force generating capacity1,2. Recently, Novikov et al. developed a model that relates time-dependent transverse diffusion to muscle fiber size from stimulated echo diffusion tensor imaging (DTI) called the random permeable membrane model (RPBM)3. The underlying assumptions for RPBM are: 1) muscle fibers are polygonal structures of varying shape and size and 2) the sarcolemma is the predominant structure that restricts the diffusion of water in a tissue. Previous studies have demonstrated RPBM is sensitive to muscle microstructural changes, however fiber size is routinely underestimated compared to histology4–7. In silico modeling allows for the precise control over simulated fiber size and geometry in order to carefully evaluate the relationship between muscle microstructure and DTI-derived RPBM outputs. Therefore, the goal of this study was to evaluate the accuracy of RPBM in predicting muscle fiber size in histology informed models of healthy and injured skeletal muscle from simulated DTI data.METHODS
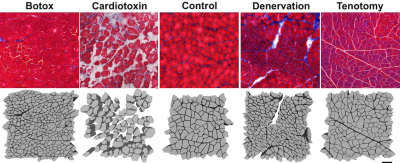
Models with histology informed geometry were derived from control, botox injected, cardiotoxin injected, surgically denervated, and surgically tenotomized rat tibialis anterior muscles 1, 3, 7, 14, and 30 days after injury (Figure 1). The MRI simulation tool DifSim was used to simulate DTI experiments in histologically informed models of skeletal muscle at varying diffusion times. DifSim employs MCell, a Monte Carlo simulator for cellular microphysiology, to simulate the diffusion of particles, and tracks particle location, signal amplitude and phase, with respect to a specified MR pulse sequence, within a user-defined, arbitrarily complex model8. A stimulated echo DTI pulse sequence was simulated, with the following sequence parameters: TE=21.76ms; b=500s/mm2; voxel size=200×200×200μm3; directions=15; =2ms; =20ms, 30ms, 40ms, 50ms, 90ms, 130ms, 170ms, 250ms, 325ms, 400ms, 500ms, and 750ms.The diffusion tensor was calculated using AFNI.The RPBM model and its implementation have been extensively discussed in Novikov et al3 and Fieremans et al7. For each injury model, radial diffusivity at each Δ and derived from DifSim were used as inputs to RPBM. From this model the free diffusion coefficient (D0), the characteristic time scale associated with a single membrane (τ), and the effective “volume fraction” ζ were fit using nonlinear least squares analysis. From these parameters, surface area to volume ratio (S/V) and fiber size (a) were derived:
$$S/V = 2ζ/sqrt(D_0*τ) [EQN 1]$$
$$a = 2sqrt(D_0*τ)/ζ = 4/(S/V) [EQN 2]$$
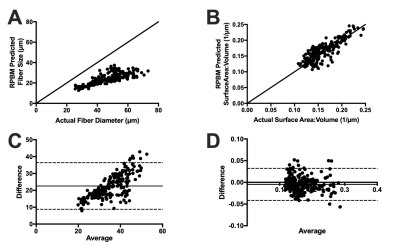
RPBM predicted fiber size and S/V were compared to actual fiber size and S/V obtained from histology via Bland Altman analysis.
RESULTS
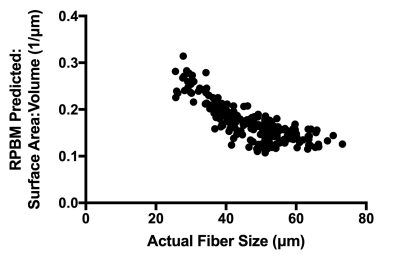
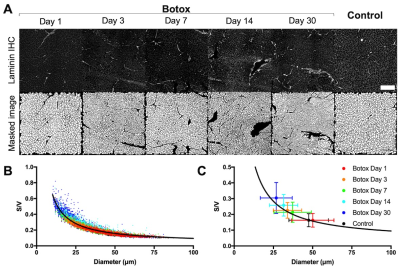
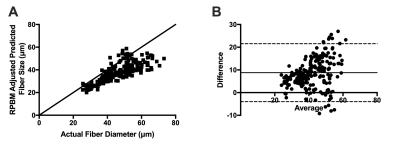
RPBM systematically underestimated fiber size compared to the actual diameter of the muscle fibers in the model for each voxel, with a bias of 22.6μm±7.1μm (Figure 2A, C). However, RPBM was found to accurately predict actual S/V of the muscle fibers simulated in this study (Figure 2B, D). When actual fiber diameter was compared to the RPBM estimated S/V of each model, an inverse relationship between the two variables was observed (Figure 3).To investigate the potential relationship between fiber diameter and S/V over a physiologically relevant range of fiber sizes in healthy and injured muscle, a supplementary analysis was performed on 14,221 muscle fibers with geometry extracted from histology of control and a botox injury model at acute and chronic timepoints after injury (Figure 4A). An inverse relationship was found between S/V and fiber diameter ($$$=6.29/(S/V)$$$), with nonlinear regression explaining 89.5% of the variance in the model respectively (Figure 4B, C). When using this modified relationship to calculate fiber size using RPBM, better agreement between RPBM-predicted and actual fiber size was found (Figure 5A), although there was still a 8.8μm±6.5μm bias towards smaller fiber sizes (Figure 5B).
DISCUSSION
The RPBM model was found to systematically underestimate muscle fiber size, but accurately estimate S/V ratio of muscle fibers. When directly compared, RPBM predicted S/V ratio appeared to be inversely related to the actual fiber size. While the clinical interpretation of S/V ratio is unclear, this indicates that accurate measurement of S/V may serve as a proxy to changes in muscle fiber size and therefore function. Although, the dynamic range of S/V was greatest for fiber diameters less than 50μm, indicating that S/V may be more sensitive to muscle atrophy than hypertrophy. Additionally, a supplemental analysis revealed that the equation $$$fiber size=6.29/(S/V)$$$ provides a more accurate estimate of fiber size from S/V than equation 2.CONCLUSION
RPBM is a useful tool to estimate underlying muscle microstructural features from time-dependent DTI measurements. RPBM was found to accurately predict S/V of muscle fibers and is inversely correlated with fiber size. However, future work is needed to determine if S/V is a functionally-relevant measurement of muscle microstructure and physiology/function. Finally, the sub-analysis in this study determined a better conversion from S/V to fiber size measurements, which may increase the accuracy of RPBM for estimating muscle fiber size.Acknowledgements
This work was supported by the NIH (R01AR070830)References
1. Krivickas LS, Dorer DJ, Ochala J, Frontera WR. 2011. Relationship between force and size in human single muscle fibres. Exp. Physiol. 96(5):539–547.
2. Fitts RH, McDonald KS, Schluter JM. 1991. The determinants of skeletal muscle force and power: Their adaptability with changes in activity pattern. J. Biomech. 24:111–122.
3. Novikov DS, Fieremans E, Jensen JH, Helpern JA. 2011. Random walks with barriers. Nat. Phys. 7(6):508–514.
4. Winters K V., Reynaud O, Novikov DS, et al. 2018. Quantifying myofiber integrity using diffusion MRI and random permeable barrier modeling in skeletal muscle growth and Duchenne muscular dystrophy model in mice. Magn. Reson. Med. 80(5):2094–2108.
5. Sigmund EE, Novikov DS, Sui D, et al. 2014. Time-dependent diffusion in skeletal muscle with the random permeable barrier model (RPBM): application to normal controls and chronic exertional compartment syndrome patients. NMR Biomed. 27(5):519–528.
6. Fieremans E, Novikov DS, Sigmund EE, et al. 2011. In Vivo Measurement of Membrane Permeability and Fiber size in Calf Muscle Using Time-dependent DWI. Ismrm 19:2011.
7. Fieremans E, Lemberskiy G, Veraart J, et al. 2017. In vivo measurement of membrane permeability and myofiber size in human muscle using time-dependent diffusion tensor imaging and the random permeable barrier model. NMR Biomed. 30(3):e3612.
8. Balls GT, Frank LR. 2009. A simulation environment for diffusion weighted MR experiments in complex media. Magn. Reson. Med. 62(3):771–778.
Figures