Introduction

There is little data to inform physicians about the risk of growth and spontaneous rupture of small (<7mm) intracranial aneurysms (IAs), more effort is needed to be put into exploration to propose an effective biomarker that could predict the evolution and possible rupture risk associated with small aneurysms. One of the factors involved in the lack of usable metrics to predict IA growth or rupture may lie in the nature of the parameters derived from MRV data. When we investigated the spatial stationarity in velocity streamlines¹, we noticed that in each of the small IAs the stationary pattern included a clearly visible vortex. Spatial stationarity in the 3D rotational flow pattern may have relevant implications on the physiopathology of aneurysm development, thus it is desirable to have a robust characterization method. Multiple metrics have been proposed to quantify vortices in fluid dynamics. However, majority of these are in CFD simulations², involving turbulence at a scale too small for MRV detection. Also, in most cases vortical metrics are calculated either within an axial plane arbitrarily chosen in the 3D vortex, which implies some dependence on user’s intervention or for each 3D spatial point that only reflects the local rotational strength. We observed in our 4D Flow MRI patients’ data that the overall 3D vortex pattern was always organized around a dominant rotational axis, and here we introduce an approach that not depends on the arbitrary choice of a 2D plane by user to account for the 3D vortex structure as a whole with determining the main axis of its rotation and its rotation center.

Methods

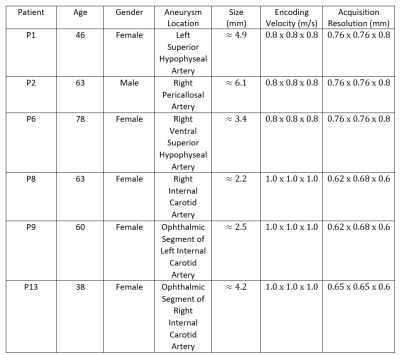
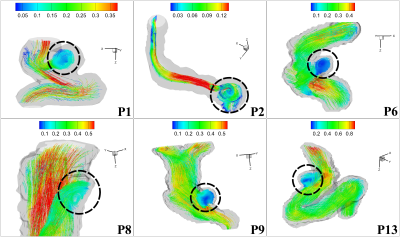
4D Flow MRI³ velocity vector data from 6 subjects obtained at 7 Tesla (Siemens, Erlangen, Germany) (Figure 1) were averaged over all cardiac phases individually to generate the cycle-averaged stationary velocity vector with increasing SNR, which were used to apply our vortex identification approach. Figure 2 shows the stationary streamlines pattern and explicit vortex structure of 6 subjects. The computations were conducted in Python and Matlab^TM, while the visualization was realized in Tecplot^TM. We extended the previously proposed scalar $$$\Gamma_{2}$$$⁴ that only identifies the rotational motion in a two dimensional plane to the vector $$$\overrightarrow{\Gamma_{2}}$$$ that works for a three dimensional flow field.
Method1: $$$\overrightarrow{\Gamma_{2}}$$$ identifies the region dominated by the rotational flow over the shear flow.
Method2: $$$\Omega$$$ and $$$\overrightarrow{\omega}$$$ capture the region where the vorticity overtakes the deformation⁵.
Approach: $$$\overrightarrow{\Gamma_{2}}$$$ and $$$\Omega$$$ were respectively computed for each spatial point in the blood flow domain defined by the aneurysm mask. The values of the magnitude of $$$\overrightarrow{\Gamma_{2}}$$$ or $$$\Omega$$$ (over a threshold) were used to define a high vortex motion region with the region growing. The spatial average of these identification vectors over the defined high vortex motion region were used to yield two vector candidates to define the main vortex motion direction. $$$\overrightarrow{\Gamma_{1}}$$$ is a vortex center identification method that we separately apply based on each of the two previously obtained averaged vortex motion directions. The resulting main vortex motion center was then assigned the corresponding averaged vortex identification vectors.

Results

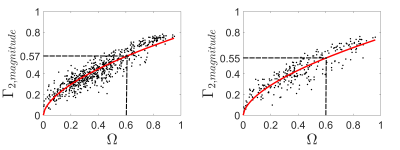
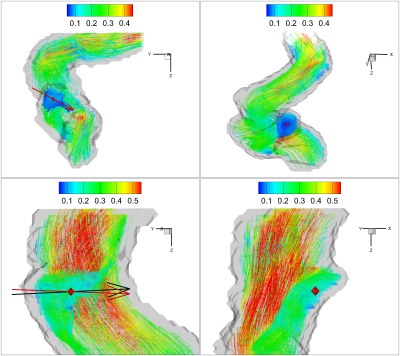
Figure 3 shows the scatter plot of the magnitude $$$\Gamma_{2,magnitude}$$$ and $$$\Omega$$$ inside aneurysm sac for two representative cases P6 and P8. The threshold used for $$$\Omega$$$ is chosen as $$$0.6$$$ to determine the threshold of $$$\Gamma_{2,magnitude}$$$. The determined threshold of $$$\Gamma_{2,magnitude}$$$ by the nonlinear regression model varies through cases but all are over $$$0.5$$$. The corresponding defined high $$$\Gamma_{2,magnitude}$$$ and $$$\Omega$$$ regions are shown in Figure 4. The volume ratio of the defined high $$$\Gamma_{2,magnitude}$$$ region to high $$$\Omega$$$ region is around $$$1$$$. (P6: $$$1.13$$$; P8: $$$1.12$$$). Figure 5 shows the results of the proposed vortex identification approach applied to these two aneurysm cases. For each case, the two different methods generate different main vortex directions ($$$\overrightarrow{\Gamma_{2}}$$$: black arrow, $$$\overrightarrow{\omega}$$$: red arrow), but both of them locate the same main vortex center based on $$$\overrightarrow{\Gamma_{1}}$$$, which is denoted by the red diamond. The respective positions of the three dimensional vortex center in both cases are well located with this approach. We can see in first case, these two main vortex vectors are fairly indistinguishable from each other, while also the angle between these two vectors in second case are small. This minute discrepancy indicates that the magnitude of $$$\overrightarrow{\Gamma_{2}}$$$ is a feasible scalar to capture the high vortex motion, and the three dimensional main vortex identification approach based on proposed $$$\overrightarrow{\Gamma_{2}}$$$ vector method is comparable to the $$$\Omega/\overrightarrow{\omega}$$$ method.

Discussion/Conclusion

Our proposed approach based on two different methods ($$$\overrightarrow{\Gamma_{2}}$$$ and $$$\Omega/\overrightarrow{\omega}$$$) is an effective way to quantify the strong vortex motion and gives the dominant axis around which the three dimensional main vortex motion rotates as a whole as well as its center. The magnitude of the new defined three dimensional $$$\overrightarrow{\Gamma_{2}}$$$ vector can be used as a good parameter to define the high vortex motion region. The fact that the angle between the two different main vortex vectors varies through cases is potentially associated with the existence of different flow hemodynamic environment and flow property inside the aneurysm sac, which may play as a key biomarker in determining the evolution of small aneurysms.

Acknowledgements

NIH grants: P41 EB027061, P30 NS076408.