1044

Gradient Optimization (GrOpt) Toolbox: A Software Package for Fast Gradient Waveform Design
Michael Loecher1,2, Matthew Middione1,2, and Daniel B Ennis1,2,3,4
1Radiology, Stanford, Palo Alto, CA, United States, 2Radiology, Veterans Administration Health Care System, Palo Alto, CA, United States, 3Cardiovascular Institute, Stanford, Palo Alto, CA, United States, 4Center for Artificial Intelligence in Medicine & Imaging, Stanford, Palo Alto, CA, United States

Synopsis

Objective: To introduce and demonstrate a software library for time-optimal gradient waveform optimization for a wide range of applications. The software allows for direct just-in-time gradient waveform design on scanner hardware for multiple vendors. The software is tested over a range of constraints and acquisition types for which compute times are on the order of (1-100ms). The sequences are also implemented on two different vendor scanners, demonstrating the interoperability of the method.

Introduction

Gradient waveforms for magnetic resonance imaging (MRI) have traditionally been designed using analytical and/or ad hoc methods. These methods work well for their designed applications, though in many cases are not time-optimal, or are not easily translated to other sequences and acquisition strategies.

An alternative to this style of analytical or ad hoc methodology is to generate gradient waveforms via a numerical optimization algorithm. These methods solve a constrained optimization problem to generate time-optimal gradient waveforms. A wide range of research has shown that these methods produce shorter duration waveforms, or waveforms confer artifact reduction, mitigate peripheral nerve stimulation (PNS), or limit eddy currents, concomitant field gradients, and gradient heating [1-8].

While these optimized gradient waveforms are almost always superior or equivalent to conventional waveform designs, usage has often been limited due to complications with implementation. Previous optimization work has either been: 1) specifically tailored for a particular acquisition type; and/or 2) optimization times have taken minutes, which makes on-the-fly usage in the clinic infeasible. This work introduces an open-source software toolbox called GrOpt (Gradient Optimization), which addresses these issues. The toolbox contains a variety of flexible constraints that can be combined to make a wide range of pulse sequences and the optimization has been heavily accelerated so that waveforms can be computed on the order of milliseconds, allowing on-the-fly computation in a clinical setting.

Software

The GrOpt software package can be found at github.com/mloecher/gropt.

Waveforms are designed by providing a set of constraints that define a given acquisition. These include:
  • Maximum gradient amplitude
  • Maximum gradient slew rate
  • Gradient moments (any order)
  • Peripheral nerve stimulation
  • Eddy current time-constant nulling
  • Diffusion b-value maximization
  • Maxwell field minimization

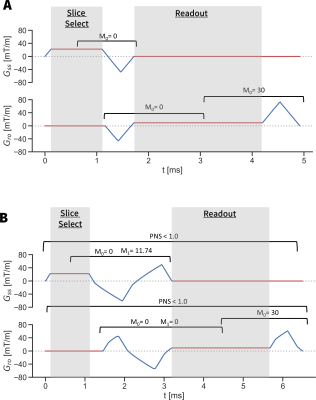
These constraints can be selected in any combination, and can be applied only to a specific duration of the waveform if necessary (i.e. a flow compensated phase encode could be designed before readout, while a spoiler gradient could be designed afterwards). Figure 1 shows an example of how GrOpt is used while Figure 2 shows a depiction of how constraints can be used to define acquisition requirements.

The solver is based on the Chambolle-Pock primal dual algorithm [9]. The dual problem is designed to check gradient amplitudes, and a stack of all other constraints and the objective function (e.g. b-value) if there is one. The optimization gradient steps are quickly computed with proximal gradients, which for inequality constraints is computationally efficient and requires only a single vector or matrix multiplication and a clipping operator.

The software is written in C for compatibility with standard scanner pulse sequence environments. Matlab and Python wrappers are also provided to facilitate prototyping and research.

Methods

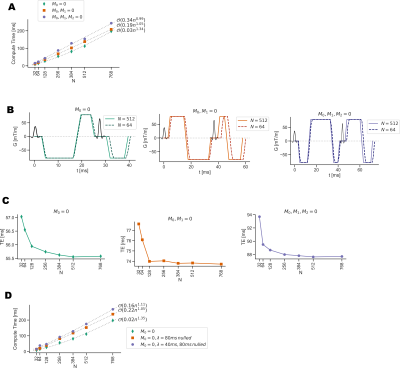
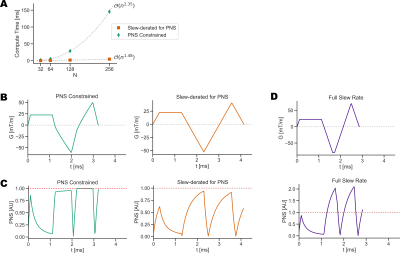
Compute times were tested for diffusion waveforms with different gradient moment compensation schemes for motion robustness (M0, M0+M1, M0+M1+M2). Additionally the temporal resolution of the waveform was varied by controlling N, the number of sampled points in the gradient waveform. The compute time was measured, as well as temporal footprint of the waveform. The effect of adding eddy current constraints on compute time was also tested.

A similar analysis was used to evaluate using GrOpt to design flow encoding bipolar gradients for phase contrast (PC-MRI). In this example, the computational and temporal footprint effects of adding an additional PNS constraint was investigated.

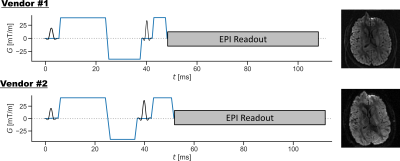
To demonstrate inter-vendor operability, GrOpt was integrated directly into diffusion pulse sequences for two vendor platforms (GE EPIC DV26.0_R01 and Siemens IDEA VE11C) using their respective pulse sequence programming environments. Optimized waveforms were generated for a b=1000s/mm2 EPI spin echo diffusion sequence, scanned in a volunteer, and the images were qualitatively compared.

Results

Figure 3 shows the results of comparing compute time with number of raster points N, degree of motion compensation, and eddy current constraints. It shows that with N=128, compute times are <50ms and the temporal resolution is high enough not to significantly affect gradient waveform durations (<0.5 ms). Figure 4 shows results from the PC-MRI evaluation. For N=64, compute times were <10ms, and there was no increased sequence timing due to the waveform temporal resolution. Figure 5 shows the waveforms and images acquired from two different scanner systems. Waveforms are similar except for timing differences due to vendor specific RF and EPI timings, and images look qualitatively similar.

Conclusion

We introduce GrOpt, a gradient optimization toolbox, and demonstrate its usage through gradient design with flexible constraints. The compute time in a variety of real world scenarios was investigated, and found to be <50ms for long diffusion waveforms, and <10ms for the shorter spatial and motion encoding gradients in PC-MRI. Implementation on multiple vendor’s hardware showed good agreement between waveforms generated, and acquired images. Future work will focus on incorporating additional constraints, further speed improvements, and implementation into a wider range of sequences directly on the scanner.

Acknowledgements

No acknowledgement found.

References

[1] O. P. Simonetti, J. L. Duerk, and V. Chankong, “MRI gradient waveform design by numericaloptimization.,” Magnetic Resonance in Medicine, vol. 29, pp. 498–504, apr 1993.

[2] B. A. Hargreaves, D. G. Nishimura, and S. M. Conolly, “Time-optimal multidimensionalgradient waveform design for rapid imaging,” Magnetic Resonance in Medicine, vol. 51,pp. 81–92, jan 2004.

[3] J. A. Derbyshire, D. A. Herzka, E. R. McVeigh, and R. J. Lederman, “Efficient implementationof hardware-optimized gradient sequences for real-time imaging.,” Magnetic Resonance inMedicine, vol. 64, pp. 1814–1820, Dec. 2010.

[4] B. D. Bolster and E. Atalar, “Minimizing dead-periods in flow-encoded or -compensated pulsesequences while imaging in oblique planes.,” Journal of magnetic resonance imaging : JMRI,vol. 10, pp. 183–192, Aug. 1999.

[5] M. J. Middione, H. H. Wu, and D. B. Ennis, “Convex gradient optimization for increasedspatiotemporal resolution and improved accuracy in phase contrast MRI,” Magnetic Resonancein Medicine, vol. 72, no. 6, pp. 1552–1564, 2014.

[6] M. Loecher, P. Magrath, E. Aliotta, and D. B. Ennis, “Time-optimized 4D phase contrastMRI with real-time convex optimization of gradient waveforms and fast excitation methods,”Magnetic Resonance in Medicine, vol. 82, no. 1, pp. 213–224, 2019.

[7] J. Sjölund, F. Szczepankiewicz, M. Nilsson, D. Topgaard, C.-F. Westin, and H. Knutsson,“Constrained optimization of gradient waveforms for generalized diffusion encoding,” Journalof Magnetic Resonance, vol. 261, pp. 157–168, 2015.

[8] E. Aliotta, H. H.Wu, and D. B. Ennis, “Convex optimized diffusion encoding (CODE) gradientwaveforms for minimum echo time and bulk motion-compensated diffusion-weighted MRI,”Magnetic Resonance in Medicine, vol. 77, pp. 717–729, feb 2017.

[9] A. Chambolle and T. Pock, “A first-order primal-dual algorithm for convex problems withapplications to imaging,” Journal of mathematical imaging and vision, vol. 40, no. 1, pp. 120–145, 2011.

Figures

Figure 1: Sample usage of the GrOpt library in Python. Parameters for the desired waveform are entered: diffusion b-value maximization, hardware constraints, M0 nulling, and the timing is related to the diffusion waveform. The optimization returns the desired waveform.

Figure 2: A depiction of (A) conventional gradient waveforms and (B) those that can be generated with constraints. Blue lines represent gradients that the toolbox is generating via optimization, and red lines represent fixed slice select and readout gradients that were defined as fixed by the user. (A) Demonstrates a simple spoiled gradient echo TR, with constraints on slice-select refocusing, readout pre-winding, and spoiling in the readout direction. (B) Represents a modification of (A) to add through-plane velocity encoding for phase contrast MRI, and a PNS constraint.

Figure 3: (A) Shows the compute time of diffusion encoding gradient waveforms in relation to the number of computed gradient points. (B) Shows the actual output waveforms from N=512 and N=64. (C) Shows the TE that would be achieved for a given N. (D) Shows the compute times in relation to N with M0 compensation and different eddy current nulling options.

Figure 4: Flow gradient waveforms with M1 = 11.74mT ms2/m corresponding to Venc = 100 cm/s, Gmax = 80 mT/m, and SRmax = 200 T/m/s. (A) Shows the compute time of a flow encoding gradient waveform in relation to the number of computed gradient points, with and without a PNS constraint. B) Shows the waveforms with and without the PNS constraint. (C) Shows plots of the PNS of the output waveforms.

Figure 5: Diffusion encoding gradient waveforms and magnitude images from the imaging experiments. The actual gradient waveforms are plotted as exported from their respective programming environments. Non-relevant/proprietary elements of the waveform are blocked out.

Proc. Intl. Soc. Mag. Reson. Med. 28 (2020)
1044