Introduction

Simulation of MRI sequences has proven to be an invaluable tool to explore and teach the underlying physical phenomena, and to allow prototyping new sequences without requiring either access to the scanner or a wide range of phantom objects. Multiple models have been proposed, from the direct solutions of Bloch equations for a single isochromat to the Fourier-based states of Extended Phase Graphs (EPG). Although these models have been supported by multiple toolkits, those are mostly dedicated to a single model and performance is often at the price of a steep learning curve. This abstract describes a new simulation toolkit, called Sycomore, which provides a user-friendly and consistent interface in Python for five different simulation models (Bloch simulation, three variants of EPG and the Configuration Model), and is released under a permissive free software license. With a core developed in C++, additionally helped by OpenMP, Sycomore offers efficient computation of those five simulation models, even on computers not dedicated to high-performance computing. After describing the design and features of the software, sample results – along with representative runtimes – will be presented.

Design and features

The features of Sycomore can be grouped in three main parts: a unit system to define type-safe physical quantities, a set of objects common to every model (e.g. species or RF pulses), and the simulation models themselves. Including a unit system in a simulation toolkit was motivated by the fact that in most MRI textbooks and papers, the physical quantities (magnetic field strength, durations, angles, etc.) describing the basic concepts (e.g. species or pulses) are usually expressed with different SI prefixes: it is common to find ms for relaxation times, µs for pulse durations, and s/mm² for b-values. Converting between those is burdensome and error-prone. To alleviate this, Sycomore provides an explicit unit system in which quantities are defined in a way closer to their usual representation: a gradient moment can be defined as gradient=100*mT/m*ms and later converted to cgs units with the expression gradient.convert_to(G/cm*s). The unit system defines all base units of the SI and their prefixes, and also includes type checking, so that adding or converting incompatible quantities will raise errors.
The three main objects common to every model follow the high-level concepts involved in MRI sequences: RF pulses interleaved with time intervals (with or without magnetic field gradients), acting on species. The basic RF pulses are hard pulses, defined only by their flip angle and their phase; using the hard-pulse approximation, shaped pulses can however be defined by providing a function describing the pulse envelope. Time intervals are simply defined by their duration and amount of dephasing caused by gradients. Lastly, a species is defined by its relaxation rates (R₁, R₂ and R₂'=R₂*-R₂), its diffusion coefficient (for isotropic species) or diffusion tensor (for anisotropic species) and its off-resonance frequency.
Based on these simple concepts, all models provide a consistent interface with two main actions: apply_pulse and apply_time_interval. The Bloch simulation model is based on a matrix-vector formalism¹, extended to homogeneous coordinates to yield a fully matrix-based simulation. It simulates isolated isochromats and provides insights about the steady-state of a sequence through spectral analysis, but does not include diffusion. Three EPG models are provided: in order of increasing complexity (both of the sequence being modeled and of runtime), they are a 1D regular model² in which the gradient-induced dephasing in each time interval is the same, a 1D discrete model³ in which the dephasings in each time interval may vary (but are discretized, i.e. binned, to avoid numerical instability) and a 3D discrete model in which the gradients and diffusion coefficient are defined in three dimensions to simulate slice profiles and anisotropic diffusion. All three EPG models include diffusion. The last model is the Configuration Model⁴, which includes diffusion and easy simulation of off-resonance effects.

Results

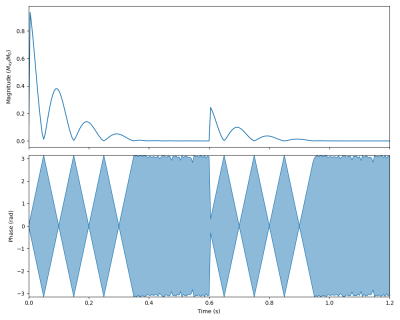
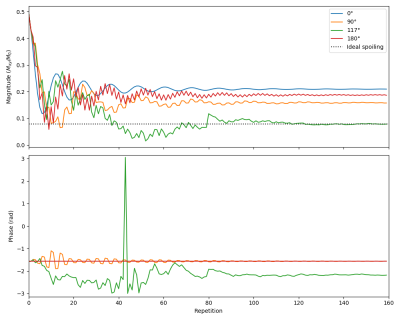
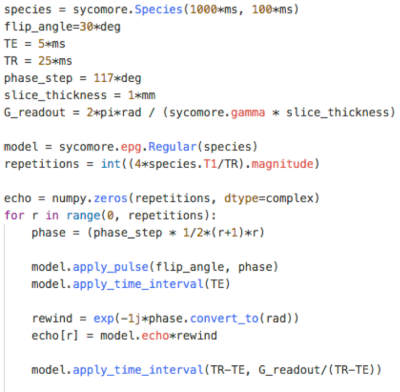
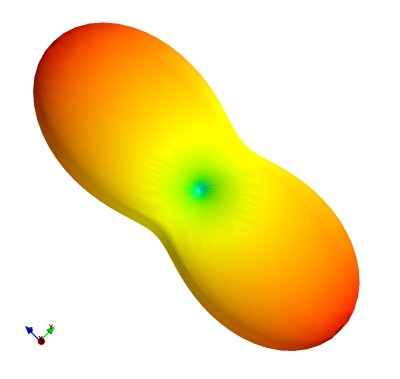
The figures showcase results of simulations on classical MRI experiments using Sycomore, as well as a code sample. Indicative runtimes on a 2015 MacbookPro are as follow (only the parameters affecting the runtimes are specified). The Bloch simulation of a RARE sequence with a time step of 5 ms and 50 isochromats (total of 12000 iterations) shown on Figure 1 takes 38 ms. The simulation of 160 repetitions of a GRE sequence with regular EPG for 4 different conditions, shown on Figure 2 takes 14 ms; the corresponding code is shown in Figure 3. The diffusion attenuation of an anisotropic species probed with 2402 gradient directions (Figure 4) takes 446 ms. All of these show that interactive runtime can be reached with simulations representative of real-life experiments.

Conclusion

Sycomore has been released under a free software license (MIT), and its source code is available on GitHub⁵. Documentation, including code samples is available on ReadTheDocs⁶, and pre-compiled packages are distributed through PyPi⁷ and Anaconda⁸. The provided models are mostly complete, but a few operators remain non-implemented: diffusion for Bloch simulation⁹, flow in EPG¹⁰ and MT for all models¹¹. In addition to implementing those missing features, future work includes adding a GPU-based computation back-end, further improving the performance in more demanding situations, e.g. sequence optimization.

Acknowledgements

No acknowledgement found.