1024
Detection of white matter hyperintensities using Triplanar U-Net ensemble network
Vaanathi Sundaresan1, Mark Jenkinson1, Giovanna Zamboni2, and Ludovica Griffanti1
1FMRIB, Wellcome Centre for Integrative Neuroimaging (WIN), Nuffield Department of Clinical Neurosciences, University of Oxford, Oxford, United Kingdom, 2Centre for prevention of Stroke and Dementia, Nuffield Department of Clinical Neurosciences, University of Oxford, Oxford, United Kingdom
1FMRIB, Wellcome Centre for Integrative Neuroimaging (WIN), Nuffield Department of Clinical Neurosciences, University of Oxford, Oxford, United Kingdom, 2Centre for prevention of Stroke and Dementia, Nuffield Department of Clinical Neurosciences, University of Oxford, Oxford, United Kingdom
Synopsis
We propose a
Introduction
White matter hyperintensities (WMHs) are localised hyperintense regions on T2-weighted and FLAIR images (hypointense on T1-weighted). Reliable and automatic detection of WMHs would help in understanding their clinical impact. Robust automated WMH segmentation is challenging due to variations in the lesion load, distribution and image characteristics. Deep learning-based convolutional neural networks (CNNs) have been shown to be reliable and provide better segmentation performance in various medical imaging applications. U-Net1, one of the most popular examples of encoder-decoder framework2 has been widely used for segmentation of various lesions in brain MR images. Ensemble models3,4 provide even more accurate segmentation than individual models and resist overfitting, which often occurs with complex models. In this work, we propose a triplanar U-Net ensemble network (TrUE-Net) model for WMH segmentation. TrUE-Net consists of an ensemble of three U-Nets, each applied on one plane (axial, sagittal and coronal) of the brain MR images, using a combination of loss functions that take into account the anatomical distribution of WMH. We evaluate our model on the publicly available data from the MICCAI WMH segmentation challenge5(MWSC) 2017, consisting of three different datasets, and compare the results of our method with those obtained with FSL-BIANCA6.Methods
Preprocessing: We use T1-weighted and FLAIR images as inputs for our model. We skull strip the images using FSL-BET7, correct for the effect of bias field using FSL-FAST8 and register the T1-weighted images to FLAIR using FSL-FLIRT9. We crop the FOV of the images closer to the brain and extract the 2D slices from the three planes, resized to the following dimensions: axial - 128x192, sagittal - 192x120 and coronal - 128x80 voxels.Model: In the proposed architecture (shown in fig.1a), for each plane, the 2D U-Net model takes 2D FLAIR+T1-weighted channels as input and provides the probability map in the corresponding plane. We trimmed the depth of the classic U-Net to obtain the 3-layer deep model. The initial convolutional layers of axial U-Net use 3x3 kernels, while sagittal and coronal U-Nets use 5x5 kernels (due to lower voxel resolutions in the latter two planes). We obtained the final probability map by averaging the individual probability maps from the 3 planes after resizing them back to their original dimensions. Averaging the probabilities reduces the variations in the final probabilities due to the effect of noise/spurious structures. When compared to a 3D U-Net, the triplanar architecture avoids discontinuities in WMH segmentation across the slices, captures even small subtle deep WMHs with less spatial context and provides a better edge detection, at the advantage of reduced network parameters.
Implementation: We used the Adam optimiser with epsilon=1x10-4, batch size of 8, total number of epochs=100, with an initial learning rate of 1x10-3 and reduced it by 10-1 every 2 epochs until it reached 1x10-5. We set the above parameters empirically using a trial-and-error method. We performed data augmentation by applying random combinations of the following transformations using parameters chosen randomly from the specified ranges: translation (offset=[-10,10]), rotation (θ=[-10o,10o]), random noise injection (σ2=[0.01,0.09]), Gaussian filtering (σ=[0.1,0.3]). We used the sum of voxel-wise cross-entropy (CE) loss and Dice loss as the total cost function. The CE loss aims to make the segmentation better at image-level and is biased towards detection of larger WMHs, while Dice loss works at voxel-level and aids in segmenting boundary voxels and small deep WMHs. Further, to make the CE loss more sensitive towards deep WMHs, we weighed the CE loss voxel-wise with the combination of square-root of distances from ventricles and the gray matter (Fig.1b), since the distance values (and the voxel weights) get higher in the deep areas, away from the ventricles. For 15,000 samples (3 planes), with training to validation ratio of 90:10, training took ≈125 minutes on an NVIDIA Tesla K40c GPU and prediction took ≈6.2 seconds/subject (≈45 slices).
Postprocessing: We padded the probability map back to the original size, applied the WM mask and thresholded the map at 0.5.
For evaluation, we used Dice and voxel-wise true positive rate (TPR), and performed paired t-tests on overall values and between deep and periventricular regions.
Results
TrUE-Net achieved Dice values of 0.81, 0.74 and 0.78 and TPR values of 0.78, 0.75 and 0.71 in Singapore, Utrecht and Amsterdam cohorts respectively (Fig. 2). As shown in fig.3, TrUE-Net provided higher Dice (significant in Singapore; p=0.002) and higher TPR values (significant in Singapore and Utrecht; p<0.001 and p=0.01 respectively) in periventricular regions with respect to deep ones. Also, TrUE-Net provides higher average Dice values of 0.70 and 0.77 in deep and periventricular regions, while BIANCA gives 0.57 and 0.76. BIANCA achieved Dice values of 0.74, 0.63 and 0.70, and TPR values of 0.76, 0.67 and 0.80 on Singapore, Utrecht and Amsterdam cohorts. From the comparative analysis with BIANCA, TrUE-Net provided better Dice values (significant in Amsterdam, p=0.04) and comparable TPR values (Fig 4), and provided more accurate results on visual inspection (Fig. 5).Conclusions
Our model performs better than BIANCA, is less noisy and more accurate, especially in subjects with low lesion load. Also, the model provided better delineation of periventricular WMHs and detected more deep WMHs, outperforming BIANCA in both the regions.Acknowledgements
This work was supported by the Engineering and Physical Sciences Research Council (EPSRC) and Medical Research Council (MRC) [grant number EP/L016052/1]. The Wellcome Centre for Integrative Neuroimaging is supported by core funding from the Wellcome Trust (203139/Z/16/Z). VS is supported by the Oxford India Centre for Sustainable Development, Somerville College, University of Oxford. MJ and GZ are supported by the National Institute for Health Research (NIHR) Oxford Biomedical Research Centre (BRC). LG is supported by the Monument Trust Discovery Award from Parkinsons UK (Oxford Parkinsons Disease Centre), the MRC Dementias Platform UK and the National Institute for Health Research (NIHR) Oxford Biomedical Research Centre (BRC).References
- Ronneberger O, Fischer P, and Brox T. U-net: Convolutional networks for biomedical image segmentation. In International Conference on Medical image computing and computer-assisted intervention, 2015, pages 234-241. Springer.
- Noh H, Hong S, and Han B. Learning deconvolution network for semantic segmentation. In Proceedings of the IEEE international conference on computer vision, 2015, pages 1520–1528.
- Badrinarayanan V, Kendall A, and Cipolla R. Segnet: A deep convolutional encoder-decoder architecture for image segmentation. IEEE transactions on pattern analysis and machine intelligence, 2017, 39(12):2481–2495.
- Opitz D and Maclin R. Popular ensemble methods: An empirical study. Journal of artificial intelligence research, 1999, 11:169-198.
- Kuijf HJ, Biesbroek JM, de Bresser J, et al. Standardized assessment of automatic segmentation of white matter hyperintensities; results of the WMH segmentation challenge. IEEE transactions on medical imaging, 2019.
- Griffanti L, Zamboni G, Khan A, et al. BIANCA (brain intensity abnormality classification algorithm): a new tool for automated segmentation of white matter hyperintensities. NeuroImage, 2016, 141:191-205.
- Smith SM. Fast robust automated brain extraction. Human brain mapping, 2002, 17(3):143-155.
- Zhang Y, Brady M, and Smith SM. Segmentation of brain MR images through a hidden markov random field model and the expectation-maximization algorithm. IEEE transactions on medical imaging, 2001, 20(1):45-57.
- Jenkinson M and Smith SM. A global optimisation method for robust affine registration of brain images. Medical image analysis, 2001, 5(2):143-156.
Figures
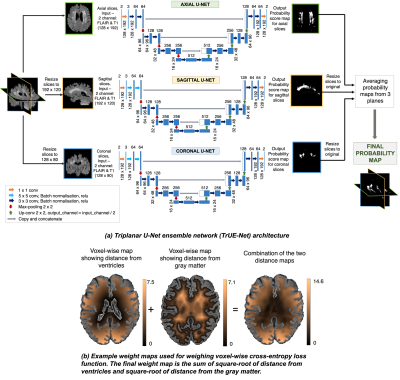
Figure 1: (a) Triplanar U-Net ensemble architecture. (b) Example weight maps used for weighing voxel-wise cross-entropy loss function.
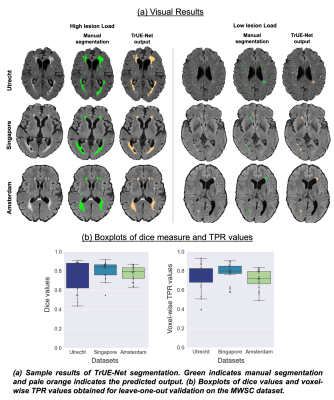
Figure 2: (a) Sample results of TrUE-Net segmentation. (b) Boxplots of dice values and voxel-wise TPR values obtained for leave-one-out validation on the MWSC dataset.
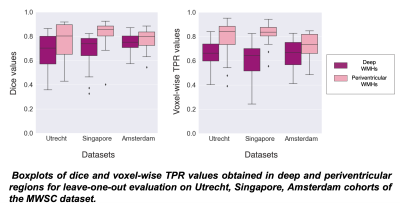
Figure 3: Boxplots of dice and voxel-wise TPR values obtained in deep and periventricular regions for leave-one-out evaluation on Utrecht, Singapore, Amsterdam cohorts of the MWSC dataset.

Figure 4: Boxplots of dice and voxel-wise TPR values obtained for TrUE-Net and BIANCA for leave-one-out evaluation on Utrecht, Singapore, Amsterdam cohorts of the MWSC dataset.
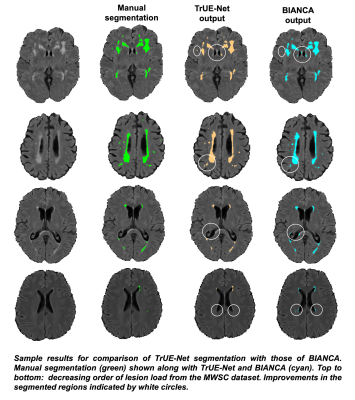
Figure 5: Sample results for comparison of TrUE-Net segmentation with those of BIANCA, in the decreasing order of lesion load from the MWSC dataset. Improvements in the segmented regions indicated by white circles.