1012

Intra-volume motion correction via Bayesian imputation in multi-parametric mapping (MPM) quantitative imaging
Mikael Brudfors1, Yaël Balbastre1, John Ashburner1, Siawoosh Mohammadi2,3, and Martina F Callaghan1
1Wellcome Centre for Human Neuroimaging, University College London, London, United Kingdom, 2Department of Systems Neuroscience, University Medical Center Hamburg-Eppendorf, Hamburg, Germany, 3Department of Neurophysics, Max Planck Institute for Human Cognitive and Brain Sciences, Leipzig, Germany

Synopsis

Intra-scan motion is a common source of artefacts in magnetic resonance imaging (MRI), which cannot be easily corrected. However, in quantitative MRI (qMRI), several volumes with varying parameters are acquired, and some sort of data redundancy exists. In this abstract, we propose a general framework where corrupted voxels are treated as missing entries and imputed using a Bayesian model of differently weighted MRI volumes. We demonstrate its efficacy in the context of various multi-parameter mapping (MPM) qMRI protocols, in which one volume is corrupted by motion. We show that the model can efficiently recover the corrupted data without introducing bias.

Introduction

Intra-scan motion is the most common cause of corruption in MRI1. It makes the complex k-space data inconsistent, which is extremely difficult to correct retrospectively, particularly if only magnitude images are available -- as is typical. Model-based correction techniques aim to (1) infer motion, (2) modify k-space lines to compensate, and (3) reconstruct the image using non-uniform Fourier transforms. More recently, (deep) learning-based methods have had success repairing highly-corrupted datasets2. Learning-based methods have the advantage of assimilating information during training that can be used to regularise subsequent reconstructions. However, such data-heavy techniques risk overfitting the training population and may therefore struggle at generalising to unseen scanning parameters3.

Here, we tackle the situation where multiple volumes, with different weighting, are acquired in one session as part of a qMRI protocol. We assume that one volume has intra-scan motion artefacts and that the affected voxels can be identified, e.g. through data consistency4. The corrupted voxel values are imputed by inference in a probabilistic generative model of such multi-channel MRI data, trained on datasets without (overt) motion-corruption.

Theory

The model used here has previously been applied to medical image translation5. It comprises two components: (1) a probabilistic tissue template that captures the spatial distribution of tissue types in the brain; and (2), a Gaussian mixture model that captures the joint intensity distributions of the MR weightings within each tissue6. Each multi-channel voxel stems from one of K Gaussian distributions (Each with distinct mean and cross-channel covariance) describing a given tissue class.

Each parameter of the model is participant-specific with population-level priors learned during training, in the form of: (1) an inverse Gauss-Wishart distribution for the Gaussian parameters; and (2), a categorical distribution for the tissue labels, encoded by the tissue template deformed by a participant-specific deformation field. If a channel is missing in a given voxel (e.g. discarded due to motion corruption), the voxel likelihood can still be defined by marginalising over the missing channel. Since the posterior distribution over unknown participant-specific quantities is intractable we approximate it using variational Bayes by assuming the posterior distribution factorises over: the joint distribution over labels and missing values; and the Gaussian parameters. This posterior distribution is then used to impute the missing values, either by taking its mean or by sampling from it5.

Methods

First, a tissue template with 14 classes (Fig.1a) was learned in an unsupervised fashion from 200 multispectral (T1- and T2-weighted) MR images from the IXI dataset (http://brain-development.org/ixi-dataset/).

Second, the model was trained using ten MPM datasets, with no visible motion artefacts, acquired on a Siemens 3T TIM Trio scanner with 1 mm isotropic resolution using the protocol described in7, consisting of calibration data and multi-echo PD-, T1- and MT-weighted spoiled gradient-echo volumes. An ESTATICS fit7 was performed yielding an R2* map and the T1-, PD- and MT-weighted signal intensities extrapolated to TE=0. These intercepts and R2* map were used for training (Fig.1b).

The fully trained model was applied to new, unseen data in two validatory experiments. Missing voxels were defined for the extrapolated MT-weighted signal at TE=0 and new values imputed by the model. These data were subsequently used to calculate an MT saturation map8:

  1. To assess bias and generalisability, the model was validated on motion-free MPM data acquired with a different 0.8mm isotropic resolution protocol described in9. 30% of the MTw intercept voxels were removed (from a cube centered in frontal cortex).
  2. The model was fit to a non-compliant participant for whom no ground truth was available. The motion corrupted voxels in the multi-echo MT-weighted volume were defined as brain voxels for which the sum of squared residuals of a log-linear fit of the decay across echo times exceeded a threshold.

Results

The learned template and covariance of the model inputs (MT, T1 and PD-weightings at TE=0ms, R2*) are shown in Fig.1. Fig.2 shows two representative sagittal planes of MT maps from the initial (a) and imputed data, either sampling from the distribution (b) or taking its mean to achieve additional denoising (c). This histogram shows that even sampling from the distribution affords a sharpening of the histogram but that no bias is introduced. Fig.3 shows the motion-corrupted MT map (a), the mask derived from the residuals of the log-linear fit to the MT-weighted volume (b), and the MT map after motion correction sampling from the distribution (c).

Discussion

The generative modelling approach proposed here imputes missing values by capitalising on a learned covariance structure. It shows generalisability by recreating data from a different protocol than was used for training, without introducing bias into the quantitative measure (Fig.2) and the capacity to successfully remove errors caused by intra-scan motion artefact (Fig.3). Additional denoising can be achieved by taking the mean of the posterior distribution. However, given that motion correction would only be applied to portions of a cohort, this may not be desirable in its present form as it would lead to non-stationary sensitivity within and between individuals. Although there is an apparent shift in the mean MT values in WM (higher MT values), we can assume this is more accurate given that no bias was observed when an uncorrupted ground truth was available (Fig.1).

Acknowledgements

MB is funded by the EU Human Brain Project's Grant Agreement No 785907 (SGA2). MFC, JA and YB are supported by the MRC and Spinal Research Charity through the ERA-NET Neuron joint call (hMRIofSCI, MR/R000050/1). The Wellcome Centre for Human Neuroimaging is supported by core funding from the Wellcome [203147/Z/16/Z]. SM was supported by ERA-NET NEURON (hMRIofSCI), the Bundesministerium für Bildung und Forschung (BMBF; 01EW1711A and B), the Deutsche Forschungsgemeinschaft (grant MO 2397/4-1), and the Forschungszentrums Medizintechnik Hamburg (fmthh; grant 01fmthh2017).

References

  1. Andre JB, Bresnahan BW, Mossa-Basha M, Hoff MN, Smith CP, Anzai Y, Cohen WA. Toward quantifying the prevalence, severity, and cost associated with patient motion during clinical MR examinations. Journal of the American College of Radiology. 2015 Jul 1;12(7):689-95.
  2. Küstner, T., Armanious, K., Yang, J., Yang, B., Schick, F., Gatidis, S., 2019. Retrospective correction of motion-affected MR images using deep learning frameworks. Magn. Reson. Med. 82, 1527–1540. https://doi.org/10/ggcg2x
  3. Knoll F, Hammernik K, Kobler E, Pock T, Recht MP, Sodickson DK. Assessment of the generalization of learned image reconstruction and the potential for transfer learning. Magnetic resonance in medicine. 2019 Jan;81(1):116-28.
  4. Callaghan, M.F., Mohammadi, S., Weiskopf, N., 2016. Synthetic quantitative MRI through relaxometry modelling. NMR Biomed. 29, 1729–1738.
  5. Brudfors, M., Ashburner, J., Nachev, P. and Balbastre, Y., 2019, October. Empirical Bayesian Mixture Models for Medical Image Translation. In International Workshop on Simulation and Synthesis in Medical Imaging (pp. 1-12). Springer, Cham.
  6. Blaiotta C, Freund P, Cardoso MJ, Ashburner J. Generative diffeomorphic modelling of large MRI data sets for probabilistic template construction. NeuroImage. 2018 Feb 1;166:117-34.
  7. Weiskopf, N., Callaghan, M.F., Josephs, O., Lutti, A., Mohammadi, S., 2014. Estimating the apparent transverse relaxation time (R2*) from images with different contrasts (ESTATICS) reduces motion artifacts. Front. Neurosci. 8.
  8. Helms, G., Dathe, H., Kallenberg, K., Dechent, P., 2008. High-resolution maps of magnetization transfer with inherent correction for RF inhomogeneity and T1 relaxation obtained from 3D FLASH MRI. Magn. Reson. Med. 60, 1396–1407.
  9. Callaghan, M.F., Josephs, O., Herbst, M., Zaitsev, M., Todd, N., Weiskopf, N., 2015. An evaluation of prospective motion correction (PMC) for high resolution quantitative MRI. Front. Neurosci. 9.

Figures

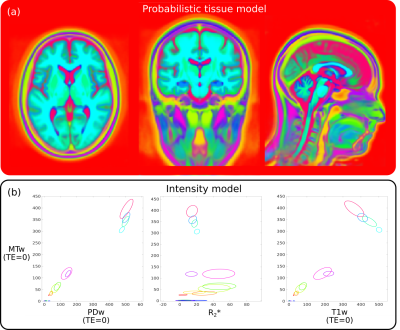
Learned tissue (a) and intensity (b) model for imputing motion-corrupted voxels in MPM data. The model was learned in an unsupervised fashion using 14 classes. The intensity model is visualised by three joint distributions with MTw on the y-axis and PDw, R2* and T1w on the x-axes. Note that the representations learned by the algorithm do not need to represent real tissues. Here, the model has been treated as a method of representing a probability density function, rather than as a way to do clustering. Any ‘meaningful’ clusters are therefore incidental.

Reference MT saturation map (a) and recalculated after imputation of the MT-weighted intercept, i.e. the value at TE=0ms (b) in conjunction with adaptive denoising (c). The excluded region for which voxels had to be recovered to generate (b) and (c) is indicated by the green box in (c). Histograms of the entire recreated region within the volume are shown in (d). Importantly, while the peaks of the histograms are sharpened--even in the case of no overt denoising--no biases are introduced.

An MT map was constructed from an MPM dataset in which the MT-weighted volume was corrupted by visible motion artefacts (a). Thresholding the root mean squared error over echo times of the log-linear fit to the multi-echo decay of the MT-weighted volumes identified erroneous voxels in the intercept (TE=0) (b), which were imputed using the proposed model. MT maps created from these corrected data are largely free of motion artefact within these voxels (c, green arrows). The histogram shows the MT values inside the residuals-based mask (d).

Proc. Intl. Soc. Mag. Reson. Med. 28 (2020)
1012