1006

Unrolled Physics-Based Deep Learning MRI Reconstruction with Dense Connections using Nesterov Acceleration

Seyed Amir Hossein Hosseini^1,2, Burhaneddin Yaman^1,2, Steen Moeller², Kamil Ugurbil², Mingyi Hong¹, and Mehmet Akcakaya^1,2
¹Electrical and Computer Engineering, University of Minnesota, Minneapolis, MN, United States, ²Center for Magnetic Resonance Research, University of Minnesota, Minneapolis, MN, United States

Synopsis

Numerous studies have recently employed deep learning (DL) for accelerated MRI reconstruction. Physics-based DL-MRI techniques unroll an iterative optimization procedure into a recurrent neural network, by alternating between linear data consistency and neural network-based regularization units. Data consistency unit typically implements a gradient step. We hypothesize that further gains can be achieved by allowing dense connections within unrolled network, facilitating information flow. Thus, we propose to unroll a Nesterov-accelerated gradient descent that considers the history of previous iterations. Results indicate that this method considerably improves reconstruction over unrolled gradient descent schemes without skip connections.

Introduction

Lengthy acquisition times remain a limitation for MRI^1-3. Deep learning (DL) has been proposed to improve fast MRI reconstruction. Physics based DL-MRI, which incorporates the known encoding operator into reconstruction, has emerged as a DL-MRI method with interpretable properties^4-6. In these approaches, an optimization procedure for solving an objective function, such as proximal gradient descent, is unrolled for a finite number of iterations. This unrolled network alternates between data consistency and regularization, and is trained end-to-end with a loss defined over the final output of the network. Most commonly, the data consistency unit is implemented as a gradient step, leading to a simple feed-forward unrolled architecture. We hypothesize that the performance can be further improved by using dense connections within this unrolled network. To this end, we propose a Nesterov-accelerated gradient (NAG) method for optimization. In contrast to proximal gradient descent (PGD), NAG utilizes the history of all previous updates. This translates to having skip connections between unrolled iterations, leading to a highly-dense recurrent neural network (RNN) architecture.

Materials and Methods

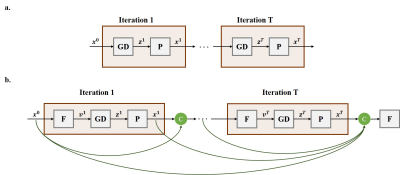
Theory: Let $$$\mathbf{x}$$$ be the image of interest, and $$$\mathbf{y}$$$ be the acquired sub-sampled k-space measurements. The forward model for a multi-coil MRI system is given as: $$(1) \quad \mathbf{y}=\mathbf{E}\mathbf{x}+\mathbf{n}$$where $$$\mathbf{E}$$$ is the encoding operator, including a partial Fourier matrix and sensitivities of the receiver coil array, and $$$\mathbf{n}$$$ represents the measurement noise². MRI reconstruction inverse problem is solved by minimizing: $$(2) \quad \arg\min_\mathbf{x} \|\mathbf{y}-\mathbf{E}\mathbf{x}\|_2^2+\cal{R}(\mathbf{x})$$where $$$\cal{R}(\mathbf{x})$$$ denotes a regularizer and the first term enforces consistency with data. This problem can be solved using PGD^6-10 as follows: $$(3) \quad \mathbf{v}=\mathbf{x}^{i-1}\\(4) \quad \mathbf{z}^i=\mathbf{v}-\mu\nabla_\mathbf{v}\|\mathbf{y}-\mathbf{E}\mathbf{v}\|_2^2=\mathbf{v}+\mu\mathbf{E}^H(\mathbf{y}-\mathbf{E}\mathbf{v}) \\(5) \quad \mathbf{x}^i=\arg\min_\mathbf{x} \|\mathbf{z}^i-\mathbf{x}\|_2^2+\cal{R}(\mathbf{x})=Prox(\mathbf{z}^i)$$where data consistency term (3) is a gradient descent step at $$$\mathbf{v}$$$ , which is set to the output of the previous iteration as in (2). A regularizer that implements a proximal operation in (4) implicitly is implemented via an artificial neural network, such as variational networks and residual networks^6,7. This algorithm is then unrolled for a fixed number of iterations, leading to the network architecture in Fig. 1a, which is subsequently trained end-to-end. The architecture in Fig. 1a is a RNN with no information flow except from the previous iteration. However, skip connections have been shown to improve performance in a number of settings¹¹. Thus, we propose a NAG method which leads to a dense unrolled RNN. NAG calculates the gradient descent step at a point based on the history of $$$k$$$ previous iterations as $$(6) \quad \mathbf{v}=\mathbf{F}(\mathbf{x}^{i-1}, \dots, \mathbf{x}^{i-k})$$ where $$$\mathbf{F}(\cdot)$$$ is the function to linearly combine previous iteration updates. The unrolled network for NAG is depicted in Fig. 1b, which is again trained end-to-end.
Methods: The two RNN architectures using PGD and proposed NAG were unrolled for $$$10$$$ iterations. In each iteration, a residual network¹² architecture with shared parameters across iterations was used to learn the proximal operator. Adam optimizer with a learning rate of $$$10^{-3}$$$, iterated over $$$100$$$ epochs with batch-size$$$=1$$$ was used to minimize a mixed normalized $$$\ell_1-\ell_2$$$ loss during training¹³. Coronal proton density (PD) knee MRI dataset from the NYU fastMRI initiative database was used to train the network with $$$300$$$ slices from $$$10$$$ subjects and to test with $$$380$$$ slices from $$$10$$$ other subjects. Data were uniformly sampled at an acceleration rate of $$$4$$$ by keeping the central $$$24$$$ lines.

Results

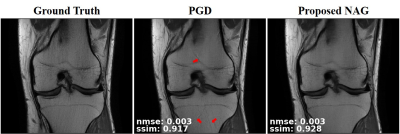
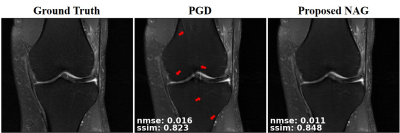
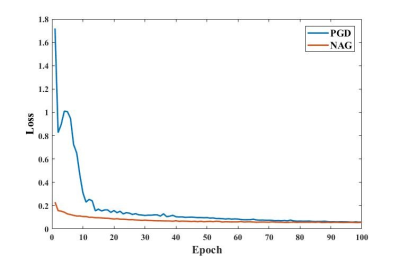
Fig. 2 and Fig. 3 respectively depict a representative slice from the coronal PD knee MRI dataset with and without fat saturation, reconstructed using PGD and proposed NAG methods. Fig. 4 plots the training loss graph for both methods in the coronal PD without fat saturation dataset. Skip connections in NAG architecture improve training loss and reduce remaining aliasing artifacts.

Discussion

We have proposed a physics-based DL MRI reconstruction technique that utilize dense RNNs based on the NAG method. To the best of our knowledge, this is the first method to use RNNs with dense connections across unrolled iterations. This novel NAG architecture utilized past updates, improving performance compared to the commonly used DL-MRI reconstruction based on PGD. The proposed approach has the potential to reduce the number of iterations for unrolling to improve computational complexity. This is important for improving practical translation, where datasets with many (>100) slices need to be reconstructed. We also note that alternative methods for data consistency based on unrolling a conjugate gradient method has also been proposed^5, albeit with more complexity and memory requirements. The utility of dense connections with a similar NAG architecture in this setting also warrants further investigation. In this study, we used a residual network for the proximal operator, but this is not a requirement and other neural networks can be utilized as well.

Conclusion

A highly-dense RNN architecture unrolled based on Nesterov’s acceleration method improves fast DL-MRI reconstruction compared to proximal gradient descent by reducing residual artifacts without requiring more computational power.

Acknowledgements

This work was supported by NIH R00HL111410, NIH P41EB027061, NIH U01EB025144, NSF CAREER CCF1651825.

References

1. Griswold MA, Jakob PM, Heidemann RM, et al. Generalized autocalibrating partially parallel acquisitions (GRAPPA). Magnetic resonance in medicine. 2002;47(6):1202–1210.

2. Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: sensitivity encoding for fast MRI. Magnetic resonance in medicine. 1999;42(5):952–962.

3. Lustig M, Donoho D, Pauly JM. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magnetic Resonance in Medicine. 58(6):1182-1195. doi:10.1002/mrm.21391

4. Schlemper J, Caballero J, Hajnal JV, Price AN, Rueckert D. A Deep Cascade of Convolutional Neural Networks for Dynamic MR Image Reconstruction. IEEE Transactions on Medical Imaging. 2018;37(2):491-503. doi:10.1109/TMI.2017.2760978

5. Aggarwal HK, Mani MP, Jacob M. MoDL: Model-Based Deep Learning Architecture for Inverse Problems. IEEE Transactions on Medical Imaging. 2019;38(2):394-405. doi:10.1109/TMI.2018.2865356

6. Hammernik K, Klatzer T, Kobler E, et al. Learning a variational network for reconstruction of accelerated MRI data. Magnetic resonance in medicine. 2018;79(6):3055–3071.

7. Mardani M, Sun Q, Donoho D, et al. Neural Proximal Gradient Descent for Compressive Imaging. In: ; 2018:9573-9583. http://papers.neurips.cc/paper/8166-neural-proximal-gradient-descent-for-compressive-imaging. Accessed November 5, 2019.

8. Mardani M, Monajemi H, Papyan V, Vasanawala S, Donoho D, Pauly J. Recurrent generative adversarial networks for proximal learning and automated compressive image recovery. arXiv preprint arXiv:171110046. 2017.

9. Gregor K, LeCun Y. Learning Fast Approximations of Sparse Coding. In: Proceedings of the 27th International Conference on International Conference on Machine Learning. ICML’10. USA: Omnipress; 2010:399–406. http://dl.acm.org/citation.cfm?id=3104322.3104374. Accessed September 16, 2019.

10. Putzky P, Welling M. Recurrent inference machines for solving inverse problems. arXiv preprint arXiv:170604008. 2017.

11. Huang G, Liu Z, Maaten L van der, Weinberger KQ. Densely Connected Convolutional Networks. In: 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Honolulu, HI: IEEE; 2017:2261-2269. doi:10.1109/CVPR.2017.243

12. Timofte R, Agustsson E, Gool LV, Yang M-H, Zhang L. NTIRE 2017 Challenge on Single Image Super-Resolution: Methods and Results.

13. Knoll F, Hammernik K, Zhang C, et al. Deep Learning Methods for Parallel Magnetic Resonance Image Reconstruction. arXiv:190401112 [cs, eess]. April 2019. http://arxiv.org/abs/1904.01112. Accessed November 5, 2019.

Figures

Figure 1. a) Proximal gradient descent (PGD) unrolled for T iterations, each consisting a data consistency (DC) unit with gradient descent at its input, followed by a proximal operation (P) for regularization. b) Proposed unrolled iterative scheme of Nesterov-accelerated gradient descent with skip connection across iterations. A 1x1 convolutional layer (F) combines outputs from previous iterations prior to the gradient descent unit (C: concatenation).

Figure 2. A representative slice from the coronal PD knee MRI dataset reconstructed using PGD and the proposed NAG methods. Skip connections in NAG architecture reduce remaining aliasing artifacts that are marked with red arrows. Quantitatively results also shows NAG outperforms PGD, although the level of improvement is comparatively less than the visible reduction of artifacts.

Figure 3. A representative slice from the coronal PD knee MRI dataset with fat saturation, reconstructed using PGD and the proposed NAG methods. Both visual and quantitative evaluation show that the proposed NAG improves reconstruction over PGD, reducing residual artifacts marked with red arrows.

Figure 4. Training loss over epochs for coronal PD knee MRI dataset for the PGD and proposed NAG methods. Notably, NAG loss is always below PGD loss and converges to its minimum faster.

Proc. Intl. Soc. Mag. Reson. Med. 28 (2020)

1006