Introduction

Recent works have explored the use of active acquisition of MRI k-space for image reconstruction with the aim of reducing scan time without compromising or being architecturally-limited in obtainable image/cine quality¹. With the advent of the these new acquisition-reconstruction pipelines, we show that motion exploiting reconstruction networks can produce reconstructions that are robust to the pipeline’s choice of undersampling mask by harnessing the entire available k-space budget.

Methods

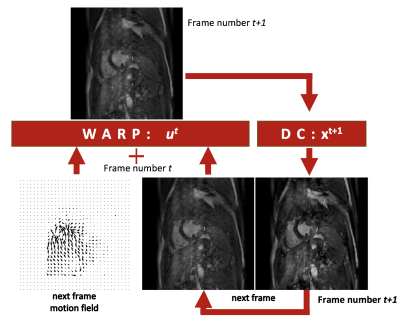
We use an ME-CNN which contains a cascade of CNNs which each contain a motion estimation block and a DC-MAC generation block as can be seen in Figure 1. The motion estimation block is used to generate a DC-MAC that is appended onto the dealiasing convolutional layers. More details about the network architecture and the DC-MAC can be found in previous work³. The DC-MAC can be formulated as an temporally-iterative data-consistency term:

$$
r^{t+1} = \mathcal{F}^{-1}\Big[(S^{t+1}\circ x^{t+1}) + ((1-S^{t+1})\circ\mathcal{F}(M^{t}r^{t}))\Big],
$$

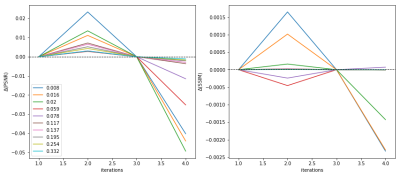
where $$$S^{t}$$$ is the undersampling mask, $$$x^{t}$$$ is the acquired k-space data and $$$M^{t}$$$ is the bilinear interpolation that warps its subject, $$$r^{t}$$$, with an optical flow, $$$\mathbf{u^{t}}$$$, which represents the motion from frame $$$t$$$ to $$$t+1$$$. The process is outlined in Figure 2. Note, the iterative algorithm is dependent on the initial frame for reconstruction, $$$r^{0}$$$, which is set to a frame $$$t'$$$ from the zero-filled reconstruction, $$$x^{t'}$$$. The term $$$y_{\text{x}}(t')$$$ is the value of $$$r^{nT}$$$ when zero-fill reconstructed frame $$$x^{t'}$$$ is used as the initial frame $$$r^{0}$$$, where $$$n$$$ is an integer and $$$T$$$ is the number of frames in the cine. In a preliminary investigation with our fully-sampled dataset and a motion-field learned by a U-Net^4-6, it was found that the DC-MAC, $$$y_{\text{x}}$$$, is optimised in terms of the SSIM and PSNR for $$$n=2$$$. This can be seen in Figure 3. One possible reason why larger $$$n$$$ causes PSNR and SSIM to drastically drop for high acceleration rates is because a k-space residue builds up in the regions of the k-space that are sampled less frequently.

Training We train ME-CNN with $$$n_{c}=3$$$ cascades end-to-end with an L2 loss on the output reconstruction of the final cascade in the network, different to the original design³. Additionally, we train the optical flow output of each cascade, $$$c$$$, against an L2 warp loss, $$$L^{f}$$$ with hyperparameter $$$\gamma=15.0$$$. The final loss function becomes:

$$
L(y, y_{gt}) = ||y - y_{gt}||^{2} + \gamma\sum_{c}^{n_{c}} L^{f}(y_{gt}; \mathbf{u_{c}}),
$$


where $$$y$$$ is the ME-CNN reconstruction output and $$$y_{gt}$$$ is the ground truth.
A previous study¹ uses the cResNet, a cascading FC-ResNet-based method to dealias static 2D images⁷. When training with a reduced parameter version of cResNet, the model heavily overfitted to our dataset. Instead, as a baseline, a DC-CNN was used as its closest model that performed reasonably². The DC-CNN consists of a series of 3 cascades of CNNs. Each CNN contains 5 convolutional layers with 96 filters each, kernel size 3 and ReLU non-linearity. Each CNN is followed by the application of data-consistency^2,3. Both DC-CNN and ME-CNN contained 2.3M parameters.

Dataset We use ten short-axis cardiac cines obtained using SSFP acqusition, 320x320mm field-of-view, 10mm slice thickness and $$$T=30$$$ frames. 32 channels were obtained and combined using SENSE reconstruction⁸ to generate a single cine. During training, we augment the dataset with a random Cartesian undersampling mask, random rotation and translation. The undersampling mask generated follows a Gaussian distribution, centred in the middle of k-space with anywhere between 3 and 85 lines acquired per frame (uniformly distributed).

Results

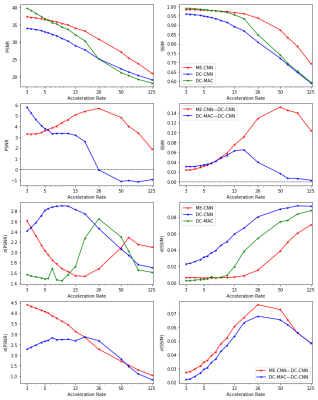
We evaluated the models on acceleration rates from $$$\times3$$$ to $$$\times125$$$ and found that ME-CNN on average performed better than DC-CNN in terms of both PSNR and SSIM as can be seen in Figure 4. Additionally, the average difference in performance for the ME-CNN compared with the DC-CNN favoured the ME-CNN. For high acceleration rates, the standard deviation of this difference was lower than the average difference at the corresponding acceleration rate. This implies a high statistical significance for claims that ME-CNN outperforms DC-CNN. An example reconstruction can be found in Figure 5. For lower acceleration rates, this claim is weaker as the average difference is lower and the standard deviation of the difference increases. However, it should be noted that for low acceleration rates, the average difference in performance for the DC-MAC compared with the DC-CNN is greater than the average difference for the ME-CNN compared with the DC-CNN. (Note: this DC-MAC is taken from the final cascade of the ME-CNN). The robustness of the DC-MAC at these low acceleration rates leads to a low standard deviation in the difference which means that high statistical significance can be found for the claim that DC-MAC outperforms DC-CNN at these rates.

Conclusion

We present findings that demonstrate the robustness of ME-CNN and the associated DC-MAC to MRI acquisitions with a random number of acquired lines in comparison to DC-CNN which closely resembled the cResNet. The DC-MAC is able to act as an intermediate reconstruction that not only stabilises the output of the ME-CNN but for high acceleration rates, is able to extract knowledge from the entire k-space budget. Future work includes extending our method to other anatomy and for 3D+t imaging.

Acknowledgements

GS is funded by the KCL & ICL EPSRC CDT in Medical Imaging (EP/L015226/1). Additionally, this work was supported by EPSRC programme Grant (EP/P001009/1), the Wellcome EPSRC Centre for Medical Engineering at Kings College London (WT 203148/Z/16/Z) and by the National Institute for Health Research (NIHR) Biomedical Research Centre based at Guy’s and St Thomas’ NHS Foundation Trust and King’s College London. The views expressed are those of the authors and not necessarily those of the NHS, the NIHR or the Department of Health.