0998

k-t SANTIS: Subspace Augmented Neural neTwork with Incoherent Sampling for dynamic image reconstruction

Fang Liu^1,2 and Li Feng³
¹Gordon Center for Medical Imaging, Massachusetts General Hospital, Harvard Medical School, Boston, MA, United States, ²Radiology, University of Wisconsin-Madison, Madison, WI, United States, ³Biomedical Engineering and Imaging Institute and Radiology, Icahn School of Medicine at Mount Sinai, New York, NY, United States

Synopsis

A novel deep learning-based dynamic image reconstruction technique called k-t SANTIS (Subspace Augmented Neural neTwork with Incoherent Sampling) is presented in this study. Different from prior deep learning-based reconstruction approaches that rely primarily on data-driven learning, k-t SANTIS incorporates a low-rank subspace model into the deep-learning reconstruction architecture, which is implemented by adding a subspace layer to enforce an explicit subspace constraint during network training. k-t SANTIS represents a new deep image reconstruction framework with hybrid data-driven and physics-informing learning, taking additional prior knowledge available in the dataset into consideration during the training process to achieve better reconstruction performance.

INTRODUCTION:

Various deep learning-based image reconstruction approaches have been demonstrated for both static image and dynamic image reconstruction in the past few years (1–5). In most of these approaches, the reconstruction of undersampled images is performed through a convolutional neural network (CNN) that relies primarily on data-driven learning (e.g., to learn latent image features from a large database). In addition to image features, MR datasets also present physics-informed prior knowledge, such as image sparsity or low-rank structure. Although this knowledge is extensively exploited in conventional reconstruction (6–10), their use in deep learning-based reconstruction is limited. In this study, we aimed to demonstrate that deep learning-based dynamic image reconstruction can benefit from incorporation of MR physics-related knowledge. More specifically, we propose and demonstrate the initial feasibility of a novel deep dynamic image reconstruction method called k-t SANTIS (Subspace Augmented Neural neTwork with Incoherent Sampling), in which a subspace layer is embedded into the neural network architecture to enforce low-rank subspace modeling during training.

METHODS:

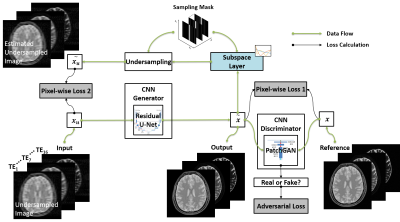
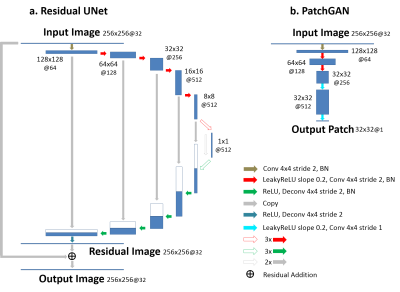
(a) Subspace Augmented Neural Network: The concept of subspace has been well-explored in iterative reconstruction. Based on the knowledge that a dynamic image-series typically contains extensive temporal correlations, the dynamic information can be represented with only a few dominant temporal basis components and associated coefficients without loss of important information (11). Therefore, instead of reconstructing the entire dynamic image frames, one can reconstruct only coefficients for several dominant basis components, leading to highly-reduced degrees of freedom and thus superior reconstruction performance. Deep learning-based dynamic image reconstruction can also benefit from exploiting such low-rank structure, in combination with learning other necessary image features in the database. In the proposed k-t SANTIS technique, we add a subspace layer into the deep image reconstruction network during training, as shown in Figure 1 and highlighted in the first loss term of Equation 1. To maintain the performance of CNN-based dynamic image reconstruction, CNN mapping with spatial-temporal filters is performed on the original dynamic image series instead of subspace (Figure 1 and the second loss term of Equation 1). The detailed subspace modeling layer is illustrated in Figure 2. Equation 1 can be described as: $$\tilde{G}=arg\min_{G}(\lambda_{1}\parallel{F^{T}{\Omega}F{\Psi}^{T}_{K}V_{K}-x_{u}}\parallel_{2}+\lambda_{2}\parallel{G(x_{u})-x}\parallel_{2})\quad\quad\quad(1) $$ where $$$ x_{u}$$$ is undersampled image, $$$x$$$ is fully-sampled image, $$$G$$$ is CNN generator, $$$F$$$ is FFT operator, $$$\Omega$$$ is the undersampling mask. $$${\Psi}_{K}$$$ is the $$$K$$$ dominant basis components and $$$ V_{K}={\Psi}_{K}G(x_{u})$$$ is the corresponding coefficients in subspace. Equation 1 can also be extended to incorporate adversarial training, which is not shown here due to the limited space.

(b) Network Implementation: The network uses the Data-Cycle-Consistent GAN structure proposed as described in (12,13), which aims to solve a training objective consisting of three loss components, including i) a standard end-to-end CNN mapping loss, ii) a data fidelity loss allowing CNN output image consistent with k-space measurements, and iii) an adversarial loss enforcing high perceptional quality of reconstructed images. As shown in Figure 3, a combination of UNet (for CNN mapping) and PatchGAN (for adversarial process) was selected for constructing the network and was trained on an Nvidia Quadro P5000 card using an adaptive gradient descent algorithm with a learning rate of 0.0002 for 200 epochs.

(c) Evaluation: The evaluation was performed using single-coil dynamic image datasets simulated on a realistic MR simulator (open-source MRiLab (9) https://leoliuf.github.io/MRiLab/ ) using a multi-echo spin-echo T2 mapping sequence (16 echoes at 1.5T) in axial orientation on 20 brain models scanned in the McGill BrainWeb project (https://brainweb.bic.mni.mcgill.ca/brainweb/). The training was performed on 18 subjects, and the rest two were used for evaluation. A time-varying 1D variable density undersampling pattern (R=8) was used and 5% of central k-space lines were fully sampled in each frame for estimation of temporal basis. The training and reconstruction took ~19 hours and 4.1 sec/subject, respectively.

RESULTS:

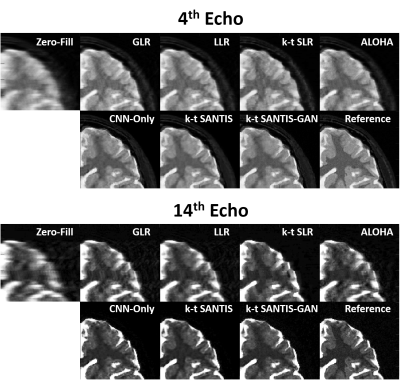
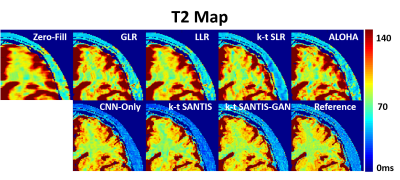
Figure 4 compares different reconstruction methods (R=8) for the 4th echo (TE=40ms) and a late echo (TE=140ms). k-t SANTIS and k-t SANTIS-GAN (k-t SANTIS with adversarial training) outperform standard CNN-based reconstruction without the subspace layer. Meanwhile, conventional iterative reconstruction (GLR(10), LLR(10), k-t SLR (6) and ALOHA (7)) failed to reliably reconstruct dynamic images at this high acceleration rate (single-coil only). The visual comparison is further confirmed by nRMSE, which was 5.5% and 5.9% for k-t SANTIS and k-t SANTIS-GAN, and 5.9%, 10.3%, 9.2%, 8.7% and 10.6% for CNN-Only, GLR, LLR, k-t SLR, and ALOHA, respectively. Figure 5 demonstrated T2 maps obtained by pixel-wise fitting of the multi-echo images. k-t SANTIS and k-t SANTIS-GAN also provided the most accurate and realistic T2 properties of different tissues with respect to the reference.

DISCUSSION:

This work presented a new deep learning-based dynamic image reconstruction technique called k-t SANTIS, which implements a subspace-augmented neural network with a newly developed subspace layer for reconstructing a highly accelerated dynamic MR dataset. The incorporation of prior knowledge (low-rank structure) available in the dataset helps improve the reconstruction performance. The proposed subspace layer is not limited to our network structure and is flexible in extending to different network structures.

Acknowledgements

No acknowledgement found.

References

1. Wang S, Su Z, Ying L, Peng X, Zhu S, Liang F, Feng D, Liang D, Technologies I. Accelerating Magnetic Resonance Imaging Via Deep Learning. In: 2016 IEEE 13th International Symposium on Biomedical Imaging (ISBI). IEEE; 2016. pp. 514–517. doi: 10.1109/ISBI.2016.7493320.

2. Hammernik K, Klatzer T, Kobler E, Recht MP, Sodickson DK, Pock T, Knoll F. Learning a Variational Network for Reconstruction of Accelerated MRI Data. Magn. Reson. Med. [Internet] 2017;79:3055–3071. doi: 10.1002/mrm.26977.

3. Zhu B, Liu JZ, Cauley SF, Rosen BR, Rosen MS. Image reconstruction by domain-transform manifold learning. Nature [Internet] 2018;555:487–492. doi: 10.1038/nature25988.

4. Schlemper J, Caballero J, Hajnal J V., Price A, Rueckert D. A Deep Cascade of Convolutional Neural Networks for Dynamic MR Image Reconstruction. IEEE Trans. Med. Imaging [Internet] 2017:1–1. doi: 10.1007/978-3-319-59050-9_51.

5. Akçakaya M, Moeller S, Weingärtner S, Uğurbil K. Scan-specific robust artificial-neural-networks for k-space interpolation (RAKI) reconstruction: Database-free deep learning for fast imaging. Magn. Reson. Med. [Internet] 2019;81:439–453. doi: 10.1002/mrm.27420.

6. Lingala SG, Hu Y, DiBella E, Jacob M. Accelerated Dynamic MRI Exploiting Sparsity and Low-Rank Structure: k-t SLR. IEEE Trans. Med. Imaging [Internet] 2011;30:1042–1054. doi: 10.1109/TMI.2010.2100850.

7. Lee D, Jin KH, Kim EY, Park S-H, Ye JC. Acceleration of MR parameter mapping using annihilating filter-based low rank hankel matrix (ALOHA). Magn. Reson. Med. [Internet] 2016;76:1848–1864. doi: 10.1002/mrm.26081.

8. Feng L, Wen Q, Huang C, Tong A, Liu F, Chandarana H. GRASP‐Pro: imProving GRASP DCE‐MRI through self‐calibrating subspace‐modeling and contrast phase automation. Magn. Reson. Med. [Internet] 2019:mrm.27903. doi: 10.1002/mrm.27903.

9. Christodoulou AG, Shaw JL, Nguyen C, Yang Q, Xie Y, Wang N, Li D. Magnetic resonance multitasking for motion-resolved quantitative cardiovascular imaging. Nat. Biomed. Eng. [Internet] 2018;2:215–226. doi: 10.1038/s41551-018-0217-y.

10. Zhang T, Pauly JM, Levesque IR. Accelerating parameter mapping with a locally low rank constraint. Magn. Reson. Med. [Internet] 2015;73:655–661. doi: 10.1002/mrm.25161.

11. Liang ZP. Spatiotemporal imaging with partially separable functions. Proc. 2007 Jt. Meet. 6th Int. Symp. Noninvasive Funct. Source Imaging Brain Hear. Int. Conf. Funct. Biomed. Imaging, NFSI ICFBI 2007 2007:181–182. doi: 10.1109/NFSI-ICFBI.2007.4387720.

12. Liu F, Samsonov A, Chen L, Kijowski R, Feng L. SANTIS: Sampling-Augmented Neural neTwork with Incoherent Structure for MR image reconstruction. Magn. Reson. Med. [Internet] 2019:1–15. doi: 10.1002/mrm.27827.

13. Liu F, Samsonov A. Data-Cycle-Consistent Adversarial Networks for High-Quality Reconstruction of Undersampled MRI Data. In: the ISMRM Machine Learning Workshop. ; 2018.

Figures

Figure 1. k-t SANTIS using a Data-Cycle-Consistent GAN structure with three loss components. The pixel-wise loss1 removes aliasing artifacts so that the reconstructed image looks like their reference. The pixel-wise loss2 ensures that the reconstructed images from the CNN generator produce undersampled images matching the acquired k-space. The adversarial loss maintains image details and texture using a CNN discriminator. An additional subspace layer (for subspace modeling) is embedded into the workflow to explore the low-rank structure of the dynamic images during training.

Figure 2. Illustration of the subspace modeling layer in the k-t SANTIS framework. In an iteration step during training, the low-resolution dynamic image series are extracted using the fully sampled k-space center of the undersampled k-space data. A temporal basis is then estimated from the low-resolution images and the first dominant K basis components are kept. A temporary output of CNN generator (e.g., UNet) is used as input of the subspace layer which is then reconstructed using only the retained K dominant basis components.

Figure 3. Illustration of the residual UNet and PatchGAN in k-t SANTIS for end-to-end CNN mapping and adversarial training. The UNet structure consists of an encoder network and a decoder network with multiple shortcut connections (e.g., concatenation) between them to enhance mapping performance. The abbreviations for the CNN layers include BN for Batch Normalization, ReLU for Rectified Linear Unit activation, Conv for 2D convolution, and Deconv for 2D deconvolution. The parameters for the convolution layers are labeled in the figure as image size @ the number of 2D filters.

Figure 4. Images at one early echo and one late echo reconstructed from different methods at R=8. The CNN-Only method improved the overall quality but still remains noticeable artifacts. k-t SANTIS generated a nearly artifact-free image with well-preserved tissue contrast compared to the reference image. k-t SANTIS-GAN maintained the same feature of k-t SANTIS and further improved the image sharpness and tissue texture. The other conventional iterative methods generated suboptimal images with either reduced image sharpness or residual artifacts at a vast undersampling rate.

Figure 5. Representative examples of T2 maps estimated from the different methods after fitting the reconstructed images. Both k-t SANTIS and k-t SANTIS-GAN generated nearly artifact-free T2 maps and k-t SANTIS-GAN further improved the image sharpness and tissue structure which closely resembles the reference tissue properties. The other iterative methods generated suboptimal T2 maps with significant bias and noticeable residual artifacts at a vast undersampling rate.

Proc. Intl. Soc. Mag. Reson. Med. 28 (2020)

0998