Introduction

Deep learning-based reconstructions (including unrolled networks) have shown great potential for efficient image reconstruction from undersampled k-space measurements, well beyond the capabilities of compressed sensing (CS)¹ with fixed transform^2-6. These reconstruction pipelines typically use the fully sampled images as the ground truth data to train the networks end-to-end with a mean-loss function over the training set. Unfortunately, the commonly used per-pixel losses (e.g., $$$l_2$$$, $$$l_1$$$ loss) don’t necessarily capture perceptual or higher-order statistical differences between the reconstructed and the ground truth images. Recent work in computer vision has shown that perceptual losses can be used to further learn high-level image feature representations⁷. However, these perceptual losses are typically designed for instance-to-class discrimination (e.g. for classification), and not designed for instance-to-instance discrimination as in MR reconstruction. In this work, we incorporate a feature representation-based loss function with existing reconstruction pipelines, which we call Unsupervised Feature Loss (UFLoss). The UFLoss provides instance-level discrimination by mapping similar instances to similar low-dimensional feature vectors. A patch-wise mapping network is trained to map the image space to the feature space, where the UFLoss corresponds to the $$$l_2$$$ loss in the feature space. We compare MoDL⁵ reconstruction results with and without our UFLoss on both 2D and 3D datasets, as well as with perceptual VGG loss. We show that the addition of the UFLoss can encourage more realistic reconstructed images with more details compared to conventional methods such as MoDL without UFloss and CS.

Methods

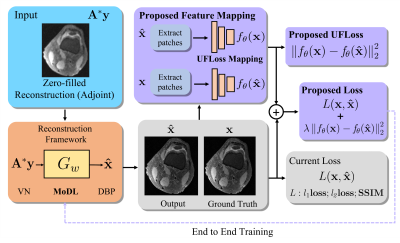
In the learning-based image reconstruction workflow (Figure 1), we added a pre-trained feature loss on top of the per-pixel loss.
Training of the UFLoss mapping network:
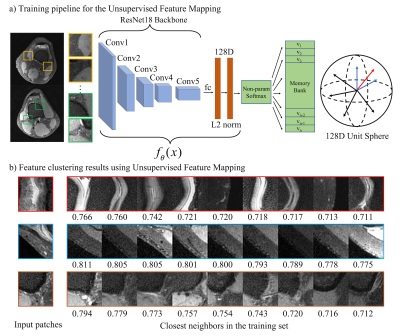
The UFLoss mapping network is trained on patches of fully sampled images in an unsupervised fashion (Figure 2.a). The training is motivated by instance-level discrimination⁸, where a feature mapping function is learned such that each patch is maximally separated from all other patches in the feature space. Suppose we have $$$n$$$ patches $$$\bf{x_1,x_2,...,x_n}$$$ in the training sets and their unit-norm features $$$\bf{v_1,v_2,...,v_n}$$$ with $$$\bf{v_i}=\it{f_{\theta}}(\bf{x})\in\mathbb{R^d}$$$. For a particular patch $$$\bf{x}$$$ with feature $$$\bf{v} = \it{f_{\theta}(\bf{x})}$$$, the probability of it being recognized as the $$$i$$$-th patch is given by the soft-max criterion: $$P(i|\bf{v})=\frac{\exp(\bf{v}_i^T\bf{v})/\tau}{\sum_{j=1}^n\exp(\bf{v}_i^T\bf{v})/\tau},$$Where $$$\tau$$$ is a temperature parameter that controls the concentration level of the distribution. The learning objective is then to maximize the joint probability $$$\Pi_{i=1}^nP_{\theta}(i|f_{\theta}(\bf{x_i}))$$$, which is equivalent to minimizing the negative log-likelihood over the training set: $$J(\theta)=-\sum_{i=1}^n\log{P(i|f_\theta(\bf{x_i}))}.$$
After training, a target patch’s nearest neighbors can be queried based on distance in the feature space (Figure 2.b). For training the feature embedding, we set $$$\tau = 1$$$ , learning rate to 0.001 and the batch size to 16.
Training MoDL with UFLoss:
We apply our UFLoss to MoDL, a recently proposed unrolled iterative network which is trained end-to-end using ground-truth images. Instead of using only the per-pixel $$$l_2$$$ loss, we add our UFLoss based on the pre-trained network, resulting in the combined loss function:$$\bf{loss(\it{\hat{x}}\bf{)}} =\it \|x-\hat{x}\|^2_2+\lambda\|f_{\theta}(x)-f_{\theta}(\hat{x})\|^2_2,$$ where $$$f_{\theta}$$$ is the feature mapping for the image, $$$x, \hat{x}$$$ are the ground truth and the reconstructed image respectively, and $$$\lambda$$$ is the parameter to control the weights on the UFLoss. All the following experiments are implemented in Pytorch , with $$$\lambda = 1$$$, learning rate 0.0005 and batch size 1.
Datasets for the experiments:
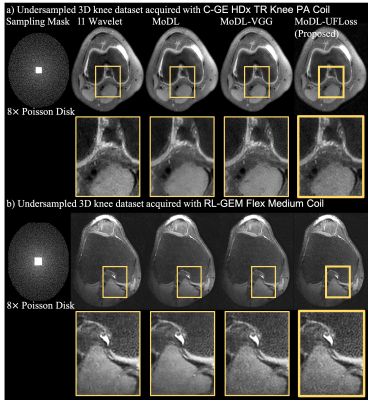
We trained and evaluated our proposed UFLoss on both 2D and 3D knee datasets. We used the fastMRI¹⁰ data for the 2D experiments. A total of 3200 slices from 200 cases were used for training. A total of 60 60$$$\times$$$60 patches were cropped from each slice (~19,000 in total) and used to train the UFLoss mapping network ($$$d=128$$$ for output). We conducted our 3D experiments on 20 Fully sampled 3D knee datasets (from mridata.org). A total of 5120 slices from 16 cases were used for training, and 40 $$$40\times40$$$ patches from each slice (~20,400 in total) were used to train the UFLoss mapping network ($$$d=128$$$ for output). In order to demonstrate the feasibility of our UFLoss on prospectively undersampled scans, we conducted 3D FSE experiments at 3T with 8x Poisson-disk sampling mask, and then used our pre-trained model to reconstruct the images. We compared the MoDL results with and without UFLoss, with the VGG loss (pre-trained on ImageNet), as well as CS reconstruction on the testing set. Peak Signal to Noise Ratio (PSNR) and the Structural Similarity Index (SSIM) were used as the metrics.

Results

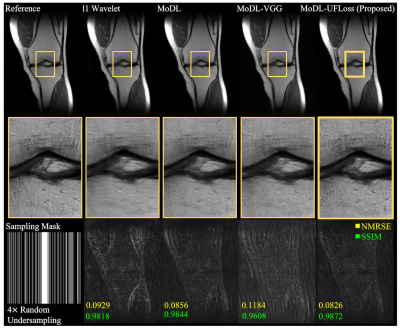
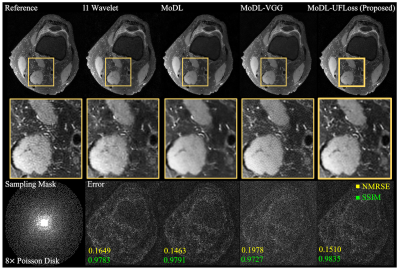
Figure 3 and Figure 4 show a representative comparison of CS, MoDL, MoDL with VGG, and MoDL with UFLoss on retrospectively undersampled 2D and 3D reconstructions respectively. The reconstructions using MoDL with UFLoss show sharper edges, higher PSNR, and higher SSIM compared to other methods with the same training epochs.
Figure 5 shows the reconstruction results on prospectively undersampled 3D knee scans, using the pre-trained model. Detailed texture and sharper edges can be seen more clearly on the reconstruction results using VGG and UFLoss.

Conclusions

In this work, we presented UFLoss, an unsupervised learned feature loss, which can be easily trained on fully sampled images offline. With the addition of UFLoss, we were able to recover texture, small features and sharper edges with higher overall image quality under the learning-based reconstruction (MoDL).

Acknowledgements

No acknowledgement found.