0990

Synchronizing dimension reduction and parameter inference in 3D multiparametric MRI: A hybrid dual-pathway neural network approach
Carolin M Pirkl1,2, Izabela Horvath1,2, Sebastian Endt1,2, Guido Buonincontri3,4, Marion I Menzel2,5, Pedro A Gómez1, and Bjoern H Menze1
1Informatics, Technical University of Munich, Munich, Germany, 2GE Healthcare, Munich, Germany, 3Fondazione Imago7, Pisa, Italy, 4IRCCS Fondazione Stella Maris, Pisa, Italy, 5Physics, Technical University of Munich, Munich, Germany

Synopsis

Complementing the fast acquisition of coupled multiparametric MR signals, multiple studies have dealt with improving and accelerating parameter quantification using machine learning techniques. Here we synchronize dimension reduction and parameter inference and propose a hybrid neural network with a signal-encoding layer followed by a dual-pathway structure, for parameter prediction and recovery of the artifact-free signal evolution. We demonstrate our model with a 3D multiparametric MRI framework and show that it is capable of reliably inferring T1, T2 and PD estimates, while its trained latent-space projection facilitates efficient data compression already in k-space and thereby significantly accelerates image reconstruction.

Introduction

Advanced multiparametric MR techniques1–4 have proven to offer reliable and accurate quantification of multiple tissue parameters from a single, time-efficient scan. The fast acquisition, however, comes at the cost of an expensive reconstruction to mitigate aliasing artifacts and low SNR due to spatial undersampling.5–7 Also, the heavy memory and computational requirements for matching the acquired signal evolutions to a precomputed dictionary are very inefficient. Multiple works, including machine learning based approaches, have been presented for accelerating parameter inference.8–10 So far, these works are generally limited to the estimation of T1 and T2 and either take the full signal evolution as input or rely on a predefined signal compression. Here we propose a hybrid dual-pathway neural network architecture that jointly learns to
  1. efficiently compress the acquired, complex signal evolutions in the time domain,
  2. reliably infer T1, T2 and PD estimates,
  3. recover the artifact-free image time-series.

Methods

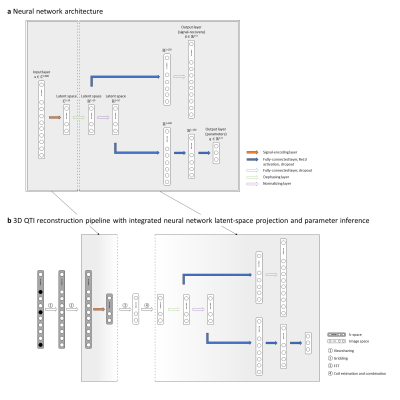
We present a proof-of-concept of our hybrid dual-pathway neural network approach for a novel 3D multiparametric quantitative transient-state imaging (QTI) acquisition which is based on the following schedule: after an initial inversion (TI=18ms), flip angles (0.8°≤FA≤70°) are applied in a ramp-up/down pattern, inspired by the scheme of Gómez et al.5, with TR/TE=10.5ms/1.8ms and 880 repetitions.
With its dual pathway design (Fig1), the model learns the non-linear relationship between the complex signal $$$\bf{x}$$$ as input, and the underlying tissue parameters $$$\bf{q}$$$, i.e. T1, T2 and a proxy for PD, together with the artifact-free signals $$$\widetilde{\bf{x}}$$$ as outputs. To synchronize dimension reduction and parameter inference, the network’s first hidden layer is a linear projection, compressing the complex signal evolution to a lower-dimensional, complex latent-space. This is followed by a phase alignment and a signal normalization layer before the network splits into its two pathways (Figure 1a): The ‘signal-recovery’ pathway specializes into a denoising encoder-decoder setup, receiving the phase-aligned latent-space representation of the signal. The ‘parametric’ pathway specializes in parameter prediction from the normalized latent-space signal. As the signal-encoding layer of our network is a linear transform, it permutes with the linear FFT and can be directly applied to the k-space data (Figure 1b), enabling fast image reconstruction in the learned lower-dimensional space. The reconstructed QTI latent-space images are then fed to the neural network for parameter inference. From the network prediction, we calculate $$$PD = \frac{||\widetilde{\bf{x}}||_2}{q_3}$$$ from the norm of the predicted signal.
Based on the extended phase graph formulism11, we created a dataset of synthetic signals for the 3D QTI scheme for T1=[100:20:4000]ms and T2=[20:4:600]ms to train our neural network and to obtain a dictionary matching reference. To train the model, we used 50% of the generated samples and added random Gaussian noise to the synthetic signals for robust training. Using ReLU activation and a parametric combination between L1 loss for parameter estimation and L2 loss for the denoising autoencoder, we trained the model with ADAM optimization (learning rate=1e-4, dropout rate=0.8, 1000 epochs).
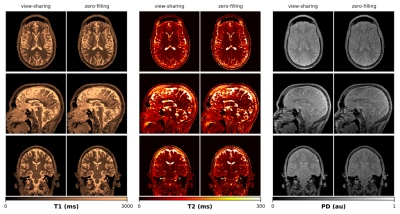
We validated our method on an in-vivo brain scan of a healthy volunteer (m, 33y), after obtaining informed consent in compliance with the German Act on Medical Devices. Data was acquired on a 3T MR750w system (GE Healthcare, Waukesha, WI) using multi-plane spiral sampling12 (55 spherical, 880 in-plane rotations) with 22.5x22.5x22.5cm3 FOV and 1.25x1.25x1.25mm3 isotropic resolution. QTI data was reconstructed using k-space weighted view-sharing13 and zero-filling, respectively. We compared our deep learning-based approach with conventional dictionary matching. For the latter, we reconstructed the QTI data using the first 10 singular images of an SVD projection14.

Results

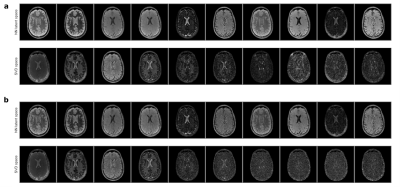
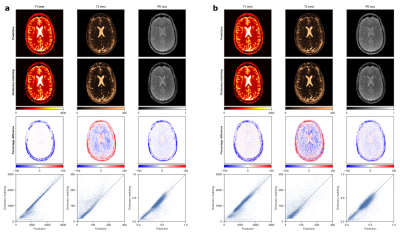
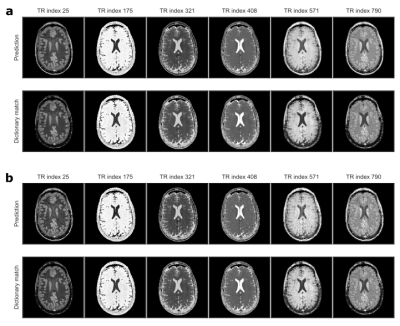
Figure 2 depicts the learned latent-space representation and the first 10 singular images of the SVD projection for comparison. As seen from Figure 3 and Figure 4, parameter maps which we obtained from the trained neural network (‘parametric’ pathway) demonstrate high image quality and are largely consistent with the dictionary matching results. In white matter, predicted T2 values are higher than the dictionary matching result. The signal curves obtained from the ‘signal-recovery’ pathway do not show visual artifacts, provide good image quality and agree well with the matched dictionary entries (Figure 5).

Discussion

We demonstrated a dual-pathway model that learns to infer T1, T2 and PD, while simultaneously recovering the artifact-free signal evolution to circumvent time- and memory-expensive dictionary matching – without being bound by dictionary size or granularity. With the signal-encoding layer, we incorporate dimension reduction into the network architecture. As such, the model can find a low-dimensional latent-space representation of the signals tailored for subsequent parameter inference. When used prior to the FFT in the reconstruction pipeline, this learned transformation allows for efficient compression already in k-space and thereby significantly reduces reconstruction time. Although the network predictions overall agree well with the dictionary matching results, it will be subject of future work to further investigate the discrepancy in low T2 values between both methods with ground truth phantom data.

Conclusion

We present a hybrid dual-pathway neural network framework that synchronizes dimension reduction and parameter estimation and addresses the reconstruction pipeline of multiparametric MRI in two ways:
  1. With the learned latent-space projection we speed up image reconstruction and
  2. efficiently infer T1, T2 and PD parameters with significantly reduced computation times and resources compared to state-of-the-art dictionary matching.

Acknowledgements

Carolin M Pirkl is supported by Deutsche Forschungsgemeinschaft (DFG) through TUM International Graduate School of Science and Engineering (IGSSE), GSC 81.

References

1. Ma D, Gulani V, Seiberlich N, et al. Magnetic Resonance Fingerprinting. Nature. 2013;495(7440):187–192.

2. Warntjes JBM, Leinhard OD, West J, et al. Rapid magnetic resonance quantification on the brain: Optimization for clinical usage. Magn. Reson. Med. 2008;60(2):320–329.

3. Cao X, Ye H, Liao C, et al. Fast 3D brain MR fingerprinting based on multi-axis spiral projection trajectory. Magn. Reson. Med. 2019;82(1):289–301.

4. Sbrizzi A, van der Heide O, Cloos M, et al. Fast quantitative MRI as a nonlinear tomography problem. Magn. Reson. Imaging. 2018;46:56–63.

5. Gómez PA, Molina-Romero M, Buonincontri G, et al. Designing contrasts for rapid, simultaneous parameter quantification and flow visualization with quantitative transient-state imaging. Sci. Rep. 2019;9(1):8468.

6. Cao X, Liao C, Wang Z, et al. Robust sliding-window reconstruction for Accelerating the acquisition of MR fingerprinting. Magn. Reson. Med. 2017;78(4):1579–1588.

7. Cruz G, Schneider T, Bruijnen T, et al. Accelerated magnetic resonance fingerprinting using soft-weighted key-hole (MRF-SOHO). PloS One. 2018;13(8):e0201808.

8. Cohen O, Zhu B, Rosen MS. MR fingerprinting Deep RecOnstruction NEtwork (DRONE). Magn. Reson. Med. 2018;80(3):885–894.

9. Gómez PA, Buonincontri G, Molina-Romero M, et al. Accelerated parameter mapping with compressed sensing: an alternative to MR Fingerprinting. In: Proc Intl Soc Mag Reson Med. Honolulu, HI, USA; 2017.

10. Balsiger F, Shridhar Konar A, Chikop S, et al. Magnetic Resonance Fingerprinting Reconstruction via Spatiotemporal Convolutional Neural Networks. In: Knoll F, Maier A, Rueckert D, eds. Machine Learning for Medical Image Reconstruction. Lecture Notes in Computer Science. Springer International Publishing; 2018:39–46.

11. Weigel M. Extended phase graphs: dephasing, RF pulses, and echoes - pure and simple. J. Magn. Reson. Imaging JMRI. 2015;41(2):266–295.

12. Cao X, Ye H, Liao C, et al. Fast 3D brain MR fingerprinting based on multi-axis spiral projection trajectory. Magn. Reson. Med. 2019.

13. Bounincontri G, Biagi Laura, Gómez PA, et al. Spiral keyhole imaging for MR fingerprinting. In: Proc Intl Soc Mag Reson Med. Honolulu, HI, USA; 2017.

14. McGivney DF, Pierre E, Ma D, et al. SVD compression for magnetic resonance fingerprinting in the time domain. IEEE TMI. 2014;33:2311–2322.

Figures

Figure 1 Neural network architecture (a) and its integration into the 3D QTI reconstruction pipeline (b). The proposed model receives the complex QTI signal time-series as input and outputs tissue parameter estimates together with the artifact-free signal curve. Being trained on synthetic signal evolutions (image space), the trained, linear signal-encoding layer can be applied on the k-space data prior to the (linear) FFT, facilitating time-efficient image reconstruction in the learned lower-dimensional latent-space.

Figure 2 Neural network latent-space representation in comparison with an SVD projection for view-sharing (a) and zero-filling (b) k-space processing. With the signal-encoding layer, we jointly train dimension reduction and parameter inference so that the neural network can find a low-dimensional latent-space representation of the QTI signals tailored for subsequent T1, T2 and PD prediction that is hence not a replicate of the SVD transform.

Figure 3 Neural network parameter inference. The proposed framework provides high quality and consistent T1, T2 and PD estimates ('parametric' pathway) for both the view-sharing and naïve zero-filling QTI image reconstruction scenario.

Figure 4 Neural network and dictionary matching parameter inference. The proposed neural network achieves a prediction quality comparable to state-of-the-art dictionary matching for both view-sharing (a) and zero-filling (b) k-space reconstruction. In white matter regions, i.e. in low T1 and T2 ranges, predicted T2 values are higher than the dictionary matching estimates. The neural network inference provides more consistent parameter estimates outside the brain.

Figure 5 Representative QTI images along the acquisition train. For view-sharing (a) and zero-filling (b) reconstruction, predicted signal curves ('signal-recovery' pathway) are consistent with the matched dictionary entries and do not show visual artifacts, providing high image quality.

Proc. Intl. Soc. Mag. Reson. Med. 28 (2020)
0990