0989
Physics-Based Self-Supervised Deep Learning for Accelerated MRI Without Fully Sampled Reference Data1Electrical and Computer Engineering, University of Minnesota, Minneapolis, MN, United States, 2Center for Magnetic Resonance Research, University of Minnesota, Minneapolis, MN, United States
Synopsis
Recently, deep learning (DL) has emerged as a means for improving accelerated MRI reconstruction. However, most current DL-MRI approaches depend on the availability of ground truth data, which is generally infeasible or impractical to acquire due to various constraints such as organ motion. In this work, we tackle this issue by proposing a physics-based self-supervised DL approach, where we split acquired measurements into two sets. The first one is used for data consistency while training the network, while the second is used to define the loss. The proposed technique enables training of high-quality DL-MRI reconstruction without fully-sampled data.
Introduction
Deep learning (DL) approaches have been proposed to improve MRI reconstruction1,2, especially using physics-based approaches that unroll an optimization algorithm incorporating the known encoding operator. These physics-based DL-MRI approaches are typically trained in a supervised manner by minimizing a loss with available ground-truth data2-5. However, in many scenarios fully-sampled acquisitions are challenging due to constraints such as organ motion, signal decay, or impractical due to long scan times. Thus, absence of fully-sampled data poses a challenge for practical translation of DL-MRI reconstruction approaches.In this work, we propose a self-supervised approach for accelerated physics-based DL-MRI reconstruction in the absence of fully-sampled data. We apply the proposed self-supervised approach on retrospectively sub-sampled knee datasets and prospectively sub-sampled brain datasets, showing it is able to successfully reconstruct images at high acceleration rates.
Theory
MRI reconstruction from under-sampled data solves the objective function$$(1)\quad \arg \min_{\bf x} \|\mathbf{y}_{\Omega}-\mathbf{E}_{\Omega}\mathbf{x}\|^2_2 + \cal{R}(\mathbf{x})$$
where x is the image of interest, $$$\mathbf{y}_{\Omega}$$$ is the acquired measurements with sub-sampling pattern $$$\Omega$$$ , E is the encoding matrix including coil sensitivities and Fourier sub-sampling, $$$\|\mathbf{y}_{\Omega}-\mathbf{E}_{\Omega}\mathbf{x}\|^2_2$$$ enforces data consistency (DC) and $$$\cal{R}(.)$$$ is a regularizer. This optimization problem is typically solved in an iterative manner, for instance using quadratic relaxation3,6,7
$$(2) \quad \mathbf{z}^{(i-1)} = \arg \min_{\bf z}\mu \lVert\mathbf{x}^{(i-1)}-\mathbf{z}\rVert_{2}^2 +\cal{R}(\mathbf{z}) \\ (3) \quad \mathbf{x}^{(i)} = \arg \min_{\bf x}\|\mathbf{y}_{\Omega}-\mathbf{E}_{\Omega}\mathbf{x}\|^2_2 +\mu\lVert\mathbf{x}-\mathbf{z}^{(i-1)}\rVert_{2}^2$$where z(i) is an intermediate variable, x(i) is the output at iteration $$$i$$$ and $$$\mu$$$ is the quadratic penalty parameter. In DL-MRI, this iterative algorithm is unrolled for fixed number of iterations, alternating between (2) and (3). An artificial-neural network (ANN) is used to implicitly solve (2) (Fig. 1). Supervised DL-MRI approaches perform end-to-end training by minimizing
$$(4) \quad \min_{\bf \theta} \frac1N \sum_{i=1}^{N} \mathcal{L}( {\bf x}_{\textrm{ref}}^i, \: f({\bf y}_{\Omega}^i, {\bf E}_{\Omega}^i; {\bf \theta}))$$where $$$\mathbf{x}_{ref}^i$$$ is ground-truth SENSE-1 image of the $$$i^{th}$$$ subject in the database, $$$f({\bf y}_{\Omega}^i, {\bf E}_{\Omega}^i; {\bf{ \theta}})$$$ denotes network output with parameters $$$\bf {\theta}$$$ for the $$$i^{th}$$$ subject, N is number of datasets in the database,and $$$\mathcal{L}(.,.)$$$ is training loss.
In our proposed approach, where fully-sampled training data is not available, we first split the data at locations $$$\Omega$$$ into two subsets:
$$(5)\quad \Omega = \Theta \cup \Lambda$$
and use the data at locations $$$\Theta$$$ for DC in the unrolled network in (3), and $$$\Lambda$$$ to define the network loss in k-space. Hence, we minimize
$$(6)\quad \min_{\bf \theta} \frac1N \sum_{i=1}^{N} \mathcal{L}\Big({\bf y}_{\Lambda}^i, \: {\bf E}_{\Lambda}^i \big(f({\bf y}_{\Theta}^i, {\bf E}_{\Theta}^i; {\bf \theta}) \big) \Big)$$
In this study, we set $$$\Theta=\Omega / \Lambda$$$. $$$\Lambda$$$ is chosen based on a variable-density Gaussian distribution. Note since $$$\Lambda$$$ has no physical constraints, it can be selected as any subset of $$$\Omega$$$ in k-space (Fig. 2).
Methods
Coronal proton density with and without fat-suppression were obtained from the NYU-fastMRI database8. Additionally, 3D MPRAGE brain MRI was acquired at 3T on ten subjects with IRB approval and written informed consent. Relevant imaging parameters: resolution=0.7×0.7×0.7mm3, FOV=224×224×179mm3, ACS lines=40, number coils=32, prospective acceleration(R)=2.Fully-sampled knee datasets were retrospectively uniformly sub-sampled at R=4, and 24 ACS lines. Prospectively-accelerated brain datasets were retrospectively further sub-sampled to R=4,6,8. Training was performed on 300 slices from 10 subjects for both knee and brain datasets. Testing was performed on 380 slices from 10 new subjects for knee and 1600 slices from 5 subjects for brain MRI.
Networks were trained using Adam optimizer with learning rates 10-3 and 5×10-4 for knee and brain MRI respectively, minimizing a mixed normalized $$$\ell_1-\ell_2$$$ loss function9 over 100 epochs. DC unit employed conjugate-gradient3. Regularizer used ResNet10. This network architecture was used for both supervised DL-MRI and proposed self-supervised framework. Further comparisons were made with CG-SENSE11 and TGV regularization12. Experimental results were quantitatively evaluated using structural similarity index (SSIM) and normalized mean square error (NMSE).
Results
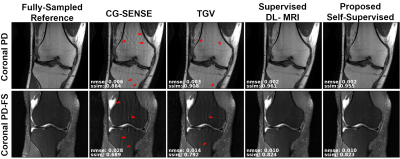
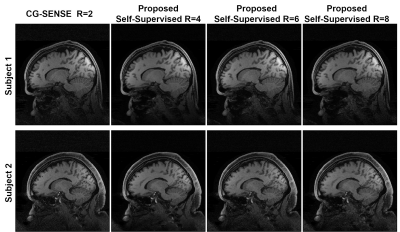
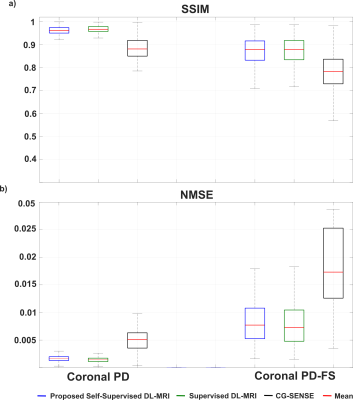
Fig. 3 shows reconstruction results for supervised DL-MRI, proposed self-supervised DL-MRI, CG-SENSE, TGV and fully-sampled reference in knee MRI. CG-SENSE and TGV suffer from residual artifacts. Both supervised and proposed self-supervised DL-MRI successfully remove these artifacts, achieving similar qualitative and quantitative improvements. Fig. 4 displays proposed self-supervised DL-MRI reconstruction results for R=4, 6, 8 in brain MRI, along with CG-SENSE R=2. Supervised DL-MRI cannot be trained here since there is no fully-sampled reference. Our proposed self-supervised approach successfully reconstructs sub-sampled brain MRI at high rates, maintaining similar quality to CG-SENSE R=2. Fig. 5 summarizes quantitative results from knee MRI.Discussion
In this study, we proposed a self-supervised training framework for physics-based DL-MRI reconstruction without using fully-sampled data. Results on knee and brain MRI show that our approach leads to improved reconstruction over other methods that do not require fully-sampled data (e.g. CG-SENSE, TGV), while having similar qualitative and quantitative performance compared to supervised DL-MRI reconstruction (trained using fully-sampled images). Other training methods without fully-sampled data have been proposed, including basis-pursuit DL13, which sequentially applies multiple DC units and iteratively updates network parameters assuming current output as the reference image. It does not use k-space loss as in our work. CycleGANs14 have also been proposed, however results are preliminary with blurring artifacts, and not been used in physics-based DL-MRI.Conclusion
Our proposed self-supervised framework enables training of high-quality physics-based DL-MRI reconstruction without fully-sampled data.Acknowledgements
Grant support: NIH P30NS076408, NIH 1S10OD017974-01, NIH R00HL111410, NIH P41EB027061, NIH U01EB025144, NSF CAREER CCF-1651825References
1. Wang S, Su Z, Ying L, Peng X, Zhu S, Liang F, Feng D, Liang D. Accelerating magnetic resonance imaging via deep learning. IEEE 13th International Symposium on Biomedical Imaging (ISBI); 2016. p 514-517.
2. Hammernik K, Klatzer T, Kobler E, Recht MP, Sodickson DK, Pock T, Knoll F. Learning a variational network for reconstruction of accelerated MRI data. Magn Reson Med 2018;79(6):3055-3071.
3. Aggarwal HK, Mani MP, Jacob M. MoDL: Model-Based Deep Learning Architecture for Inverse Problems. IEEE Trans Med Imaging 2019;38(2):394-405.
4. Lee D, Yoo J, Tak S, Ye JC. Deep Residual Learning for Accelerated MRI Using Magnitude and Phase Networks. IEEE Trans Biomed Eng 2018;65(9):1985-1995.
5. Schlemper J, Caballero J, Hajnal JV, Price AN, Rueckert D. A Deep Cascade of Convolutional Neural Networks for Dynamic MR Image Reconstruction. IEEE Trans Med Imaging 2018;37(2):491-503.
6. Qin C, Schlemper J, Caballero J, Price AN, Hajnal JV, Rueckert D. Convolutional Recurrent Neural Networks for Dynamic MR Image Reconstruction. IEEE Trans Med Imaging 2019;38(1):280-290.
7. Fessler JA. Optimization methods for MR image reconstruction. arXiv:1903.03510; 2019.
8. Zbontar J, Knoll F, Sriram A, Muckley MJ, Bruno M, Defazio A, Parente M, Geras KJ, Katsnelson J, Chandarana H, others. FastMRI: An open dataset and benchmarks for accelerated MRI. arXiv preprint arXiv:1811.08839; 2018.
9. Knoll F, Hammernik K, Zhang C, Moeller S, Pock T, Sodickson DK, Akcakaya M. Deep Learning Methods for Parallel Magnetic Resonance Image Reconstruction. arXiv preprint arXiv:1904.01112; 2019. 10. Timofte R, Agustsson E, Van Gool L, Yang M-H, Zhang L. Ntire 2017 challenge on single image super-resolution: Methods and results. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops; 2017. p 114-125.
11. Pruessmann KP, Weiger M, Bornert P, Boesiger P. Advances in sensitivity encoding with arbitrary k-space trajectories. Magn Reson Med 2001;46(4):638-651.
12. Knoll F, Bredies K, Pock T, Stollberger R. Second order total generalized variation (TGV) for MRI. Magn Reson Med 2011;65(2):480-491.
13. Sim B, Oh G, Lim S, Ye JC. Optimal Transport, CycleGAN, and Penalized LS for Unsupervised Learning in Inverse Problems. arXiv:1909.12116; 2019.
14.Tamir JI, Stella XY, Lustig M. Unsupervised Deep Basis Pursuit: Learning Reconstruction without Ground-Truth Data. Proceedings of the 27th Annual Meeting of ISMRM; 2019.
Figures