Introduction

Magnetic resonance (MR) parameter maps represent quantitative tissue characteristics such as $$$T_{1}$$$, $$$T_{2}$$$, or $$$T_2^*$$$ relaxation properties, which provide valuable diagnostic information of diseases having the potential to be used in precision medicine¹. Several methods have been proposed for acquiring MR parameter maps such as variable flip angle (VFA) method for $$$T_{1}$$$ mapping, multi-echo spin-echo method for $$$T_{2}$$$ mapping, and multi-echo gradient-echo method for $$$T_2^*$$$ mapping^2-4. However, these methods require repeated scans with different MRI scan parameters to acquire quantitative maps, which increased the scan time. In recent years, there have been several studies which applied deep-learning algorithms to MR image reconstruction; however, there is limited research in reconstructing MR parameter maps from undersampled k-space data^5-7. In this study, we proposed a Deep mOdel-based MR PArameter MappIng NEtwork termed as “DOPAMINE”, which reconstructs MR parameter maps from undersampled multi-channel k-space data using deep convolutional neural networks (CNN) and interleaved MR signal model-based data consistency schemes.

Methods

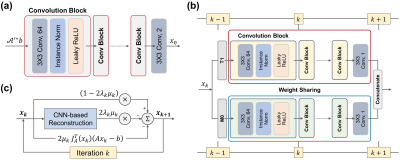
The purpose of this study was to reconstruct MR parameter maps from undersampled multi-channel k-space data using deep-learning networks. Thus, the objective function can be formulated as the following least squares equations:
$$\min\frac{1}{2}\parallel{\mathcal{A}(x)-b}\parallel^2_2 + \lambda \parallel{x-\mathcal{D}_R(x)}\parallel^2_2$$
where $$$x$$$ represents MR parameters maps, $$$b$$$ represents measured k-space data, and operator $$$\mathcal{A}$$$ has MR signal modeling $$$\mathcal{S}$$$, coil sensitivity maps $$$\mathcal{C}$$$, Fourier transform $$$\mathcal{F}$$$, and k-space sampling matrix $$$\mathcal{M}$$$, which can be represented as follows: $$$\mathcal{A}:x\mapsto\left[\mathcal{M}\cdot\mathcal{F}\left\{\mathcal{C}\cdot\mathcal{S}(x) \right\}\right]$$$. The right term of the equation is a CNN-based regularization with the trainable parameter $$$\lambda$$$ and $$$\mathcal{D}_R(x)$$$ is the output of CNN which estimates artifacts removed MR parameter maps from $$$x$$$. The least squares equations can be solved by using an iterative algorithm of gradient descent method, which is given by
$$x_{k+1}=x_k-2\mu_k[J^T_\mathcal{A}(x_k)(\mathcal{A}x_k-b)+2\lambda(x_k-\mathcal{D}_R(x_k))]$$
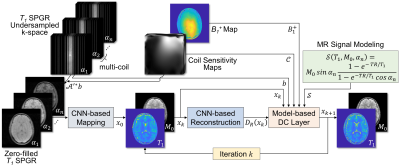
where $$$x_k$$$ is the reconstructed image at iteration $$$k$$$, $$$\mu_k$$$ is the step size at iteration $$$k$$$, $$$J_\mathcal{A}$$$ is the Jacobian matrix of $$$\mathcal{A}$$$. The $$$x_{k=0}$$$ is reconstructed by the mapping CNN which estimates initial MR parameter maps from undersampled MR images. In overall, the DOPAMINE consists of two models: 1) MR parameter mapping model which estimates initial parameter maps from undersampled k-space data with a deep CNN (CNN-based mapping), 2) parameter map reconstruction model which removes aliasing artifacts with a deep CNN (CNN-based reconstruction) and interleaved data consistency layer by embedded MR model-based optimization procedure. In this study, we demonstrated the performance of DOPAMINE with VFA model-based $$$T_1$$$ mapping. The overall architecture of DOPAMINE is presented in Fig. 1 and Fig. 2.

We used five convolution blocks for CNN-based mapping, and each convolution block consists of 2D convolution layer followed by leaky ReLU and instance normalization. The kernel size of all convolution layers is 3 and the number of feature maps is 64. For CNN-based reconstruction, we used five convolution blocks for each $$$T_1$$$ and $$$M_0$$$, and trainable weights in those blocks were shared in every iteration. A total of ten iterations was performed in parameter map reconstruction model. We implemented DOPAMINE in an end-to-end fashion. DOPAMINE was trained using an Adam optimizer for 300 epochs with an initial learning rate 0.0001, which was reduced by half in every 100 epochs.

MRI was performed using a 3.0T scanner (Ingenia CX, Philips) with a 32-channel sensitivity-encoding head coil. Data for eight subjects were acquired using spoiled gradient echo (SPGR) sequences, with five subjects’ data sets used for the training set, two for the test set, and one for the validation set. The parameters of SPGR sequence for VFA method were as follows: TR, 7.6 ms; TE, 3.2 ms; flip angle, 4, 8, and 18 degrees; matrix size, 256 $$$\times$$$ 256; pixel resolution, 0.94 $$$\times$$$ 0.94 mm²; and slice thickness, 0.94 mm. For $$$B^+_1$$$ mapping, double-angle method was used with SPGR images acquired with two different flip angles and the parameters were as follows: TR, 6000 ms; TE, 6.0 ms; flip angle, 120 and 240 degrees; matrix size, 64 $$$\times$$$ 64; pixel resolution, 3.75 $$$\times$$$ 3.75 mm²; and slice thickness, 3.75 mm. The acquired images were interpolated into the same size of SPGR images of VFA method. The coil sensitivity maps were computed from full-sampled center k-space data size of 17 $$$\times$$$ 17 using ESPIRiT method⁸. We retrospectively undersampled k-space data of VFA SPGR with a reduction factor R = 3 variable-density 1D Cartesian sampling pattern and R = 5 variable-density Poisson-disk sampling pattern.

Results

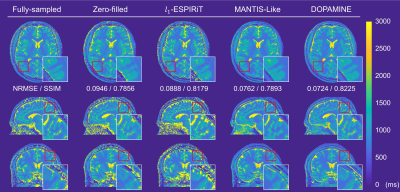
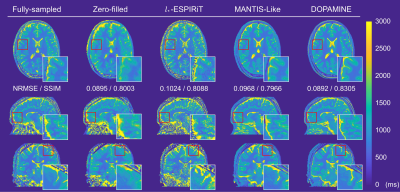
We compared DOPAMINE with the conventional methods L₁-ESPIRiT⁸ and U-net based direct mapping method (MANTIS-like)⁹. Fig. 3 and Fig. 4 shows fully sampled and reconstructed maps in axial, sagittal, and coronal slices produced by zero-filled, the two conventional methods, and DOPAMINE, with a reduction factor R = 3 variable-density 1D Cartesian and R = 5 variable-density Poisson-disk sampling patterns. DOPAMINE showed better performance than the conventional methods in removing aliasing artifacts. Furthermore, DOPAMINE showed the lowest normalized root mean square error (NRMSE) and the highest structural similarity (SSIM) values for both sampling patterns.

Conclusion

We proposed a deep model-based MR parameter mapping network termed as DOPAMINE. It was effective in reconstructing MR parameter maps from undersampled multi-channel k-space data, achieving superior performance, both quantitatively and qualitatively, over conventional methods.

Acknowledgements

This research was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Science and ICT (2019R1A2B5B01070488), Bio & Medical Technology Development Program of the National Research Foundation (NRF) funded by the Ministry of Science and ICT (NRF-2018M3A9H6081483), Brain Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Science, ICT & Future Planning (2018M3C7A1024734), and the Brain Korea 21 Plus Project of Dept. of Electrical and Electronic Engineering, Yonsei University, in 2019.