0987
Σ-net: Ensembled Iterative Deep Neural Networks for Accelerated Parallel MR Image Reconstruction1Department of Computing, Imperial College London, London, United Kingdom, 2Hyperfine Research Inc., Guilford, CT, United States, 3School of Computer Science, University of Birmingham, Birmingham, United Kingdom, 4NIH Clinical Center, Bethesda, MD, United States
Synopsis
We propose an ensembled Ʃ-net for fast parallel MR image reconstruction, including parallel coil networks, which perform implicit coil weighting, and sensitivity networks, involving explicit sensitivity maps. The networks in Ʃ-net are trained with various ways of data consistency, i.e., gradient descent, proximal mapping, and variable splitting, and with a semi-supervised finetuning scheme to adapt to the k-space data at test time. We achieved robust and high SSIM scores by ensembling all models to a Ʃ-net. At the date of submission, Ʃ-net is the leading entry of the public fastMRI multicoil leaderboard.
Introduction
The fastMRI1 multicoil challenge provides a great opportunity to show how we can push the limits of acquisition speed by combining parallel magnetic resonance imaging (pMRI) and deep learning. In this work, we present the current leading entry of the public fastMRI multicoil leaderboard: Ʃ-net. We explore different types of reconstruction networks: (1) parallel coil networks (PCNs) and (2) sensitivity networks (SNs). Following the success of learned iterative schemes2-7, we investigate different ways of data consistency (DC) and train the networks in both a supervised and semi-supervised manner. We further increase the robustness by ensembling the individual reconstructions.Methods
We explore various network architectures and learning strategies. In the following, we give a short overview of the different architectures and show how we achieve an ensembled Ʃ-net (see Figure 1).Learning Unrolled Optimization
We learn a fixed iterative scheme to obtain a reconstruction$$$~x$$$ from k-space data$$$~y$$$ involving a linear forward model$$$~A$$$ $$x^{t+\frac{1}{2}}=x^t-f_{\theta^t}(x^t),{\quad}x^{t+1}=g(Ax^{t+\frac{1}{2}},y),\quad{0}\leq{t}<T.$$ Here, $$$f_\theta$$$ represents the network-based reconstruction block, $$$g$$$ denotes a DC layer and $$$T\!\!=\!\!9$$$ is the number of steps. Each reconstruction block has the form of an encoding-decoding structure8,9. For DC, we investigate gradient descent (GD)2, proximal mapping (PM)3, and variable splitting (VS)4.
Network Architectures
We investigate two types of architectures for pMRI reconstruction, visualized in Figure 1. Parallel coil networks (PCNs) reconstruct individual coil images for $$$Q~$$$coils7. The network$$$~f_\theta$$$ is realized by a U-net8 with $$$Q~$$$complex-valued input and output channels and learns implicit coil weightings. For sensitivity networks (SNs), the coil combination10 is defined in the operator$$$~A$$$ using an extended set of $$$M{=}2$$$ explicit coil sensitivity maps as in11, to overcome field-of-view issues. In this case, the network$$$~f_\theta$$$ to reconstruct$$$~x=[x_1,x_2]$$$ has two complex-valued input and output channels and is modelled by a Down-Up network9. The final reconstruction$$$~x_{\text{rec}}$$$ is obtained by RSS combination of the individual channels of$$$~x^T$$$.
(Semi-)Supervised Learning
We trained individual networks for the acceleration factors R=4 and R=8 as well as contrasts PD and PDFS on the fastMRI1 training set. The networks were trained using a combination of $$$\ell_1$$$ and SSIM12,13 loss between the reference$$$~x_{\text{ref}}$$$ and the reconstruction$$$~x_\text{rec}\!\!=\!\!x^T$$$, involving the binary foreground mask$$$~m$$$. We trained for 50 epochs using RMSProp (learning rate 10-4). The trained model was further finetuned for 10 epochs (learning rate 5×10-5) using an LSGAN loss14. To adapt to new k-space data and overcome smooth reconstructions, we propose a semi-supervised finetuning scheme. Motivated by15, we consider the problem $$\min_\theta\frac{1}{2}\Vert Ax(\theta)-y\Vert_2^2+\frac{\alpha}{2}\max\left(\text{SSIM}(|x(\theta)|,|x_\text{rec}|)-\beta),0\right)^2,$$ where we use the initial network output$$$~x_\text{rec}$$$ as a prior. We finetune for 30 epochs on 4 slices of a patient volume simultaneously using ADAM (learning rate 5×10-5,$$$~\alpha\!\!=\!\! 1,\,\beta\!\!=\!\!0.008$$$). The trained parameters are then used to reconstruct the whole patient volume.
Experimental Setup
We trained one PM-PCN, with the individual fully sampled coil images as $$$x_{\text{ref}}$$$, and four different SNs with different data consistency layers and losses, i.e., PM-SN, GD-SN, VS-SN, GD-SN-LSGAN. Additionally, we finetuned the GD-SN, denoted as GD-SN-FT. The reference$$$~x_{\text{ref}}$$$ for the SNs was defined by the sensitivity-combined fully sampled data.
To overcome the huge memory consumption of the proposed networks, we extract patches of size 96 in frequency encoding direction. At test time, the network is applied to the full data. To stabilize training, we generated foreground masks semi-automatically using the graph cut algorithm for 10 cases, followed by a self-supervised refinement step using a U-net8.
Style-Transfer Layer (STL)
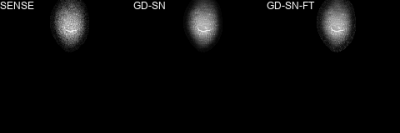
We observed that the gap between the fastMRI target RSS and non-accelerated sensitivity-weighted images is relatively large for PDFS cases as the fastMRI data were not pre-whitened16 (see Figure 2). To match the RSS background level, we replaced the background by the mean value, estimated from 100×100 noise patches of the undersampled RSS and scaled by the true acceleration factor. To bridge the gap further, we trained a STL based on a SN using SSIM loss (10 epochs, RMSProp, learning rate 5×10-5).
Ensembling
To get robust quantitative scores, we use following ensemble to form the Ʃ-net $$x_\text{rec}=m\odot(0.3\cdot{x}_\text{SN}+0.2\cdot{x}_\text{PCN}+0.5\cdot{x}_\text{SN-FT})+(1-m)\odot\frac{x_\text{SN}+x_\text{PCN}}{2}.$$ The reconstruction$$$~x_\text{SN}$$$ contains the average over the SNs excluding the GD-SN-FT, which is denoted by$$$~x_\text{SN-FT}$$$, and $$$x_\text{PCN}$$$ is the PM-PCN reconstruction. Here, $$$m$$$ is the binary foreground mask and$$$~\odot$$$ denotes the pixel-wise product.
Results
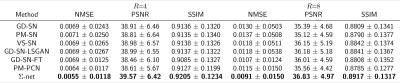
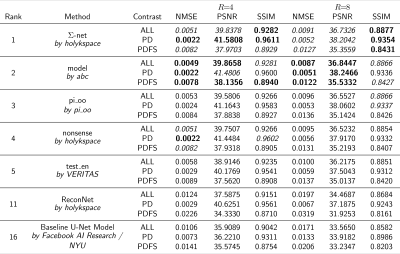
We present quantitative scores on the fastMRI1 validation set in Table 1 and qualitative results on a PDFS case for R=8 in Figure 2. The ensembled Ʃ-net achieves the best SSIM scores. While the scores of SN-FT are low, it appears most textured and sharp compared to the ensembled Ʃ-net result. The effect of finetuning SN-FT compared to SN-GT without STL is visualized in Figure 3. Ʃ-net is the current leading entry of the public fastMRI multicoil leaderboard as shown in Table 2.Discussion and Conclusion
This work presents the current leading entry of the public fastMRI1 multicoil leaderboard: Ensembled Ʃ-net of our team holykspace. The ensembling reduces random errors made by the individual PCNs and SNs. Semi-supervised finetuning adapts to the new k-space data and restores texture and noise, however, the quantitative metrics do not coincide with the visual perception. Exclusively for the fastMRI challenge, we used STL for SNs to match the contrast of the RSS target. This has no practical relevance and decreases the quality of our initial results.Acknowledgements
The work was funded in part by the EPSRC Programme Grant (EP/P001009/1) and by the Intramural Research Programs of the National Institutes of Health Clinical Center.References
1. Jure Zbontar, Florian Knoll, Anuroop Sriram, Matthew J Muckley, Mary Bruno, Aaron Defazio, Marc Parente, Krzysztof J Geras, Joe Katsnelson, Hersh Chandarana, et al. fastMRI: An open dataset and benchmarks for accelerated mri. arXiv preprint arXiv:1811.08839, 2018.
2. Kerstin Hammernik, Teresa Klatzer, Erich Kobler, Michael P. Recht, Daniel K. Sodickson, Thomas Pock, and Florian Knoll. Learning a variational network for reconstruction of accelerated MRI data. Magnetic resonance in medicine, 79:3055-3071, 2018.
3. Hemant Kumar Aggarwal, Merry Mani, and Mathews Jacob. Modl: Model-based deep learning architecture for inverse problems. IEEE Transactions on Medical Imaging, 38:394-405, 2017.
4. Jinming Duan, Jo Schlemper, Chen Qin, Cheng Ouyang, Wenjia Bai, Carlo Biffi, Ghalib Bello, Ben Statton, Declan P O’Regan, and Daniel Rueckert. VS-Net: Variable Splitting Network for Accelerated Parallel MRI Reconstruction. In International Conference on Medical Image Computing and Computer Assisted Intervention, pp. 713-722, 2019.
5. Jo Schlemper, Jose Caballero, Joseph V Hajnal, Anthony N Price, and Daniel Rueckert. A deep cascade of convolutional neural networks for dynamic MR image reconstruction. IEEE Transactions on Medical Imaging, 37(2):491-503, 2017.
6. Chen Qin, Jo Schlemper, Jose Caballero, Anthony N Price, Joseph V Hajnal, and Daniel Rueckert. Convolutional recurrent neural networks for dynamic MR image reconstruction. IEEE Transactions on Medical Imaging, 38(1):280–290, 2018.
7. Jo Schlemper, Jinming Duan, Cheng Ouyang, Chen Qin, Jose Caballero, Joseph V Hajnal, and Daniel Rueckert. Data consistency networks for (calibration-less) accelerated parallel MR image reconstruction. In ISMRM 27th Annual Meeting, p. 4664, 2019.
8. Olaf Ronneberger, Philipp Fischer, and Thomas Brox. U-net: Convolutional networks for biomedical image segmentation. In International Conference on Medical image computing and computer-assisted intervention, pp. 234-241, Springer, 2015.
9. Songhyun Yu, Bumjun Park, and Jechang Jeong. Deep iterative down-up cnn for image denoising. In IEEE Conference on Computer Vision and Pattern Recognition (CVPR) Workshops, 2019.
10. Klaas P Pruessmann, Markus Weiger, Markus B Scheidegger, and Peter Boesiger. SENSE: Sensitivity Encoding for Fast MRI. Magnetic resonance in medicine, 42(5):952-962, 1999.
11. Martin Uecker, Peng Lai, Mark J. Murphy, Patrick Virtue, Michael Elad, John M. Pauly, Shreyas S. Vasanawala, and Michael Lustig. ESPIRiT - an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA. Magnetic resonance in medicine, 71 3:990-1001, 2014.
12. Hang Zhao, Orazio Gallo, Iuri Frosio, and Jan Kautz. Loss functions for image restoration with neural networks. IEEE Transactions on Computational Imaging, 3(1):47-57, 2016.
13. Kerstin Hammernik, Florian Knoll, Daniel K Sodickson, and Thomas Pock. L2 or not L2: Impact of loss function design for deep learning MRI reconstruction. In ISMRM 25th Annual Meeting, p. 0687, 2017.
14. Christian Ledig, Lucas Theis, Ferenc Huszár, Jose Caballero, Andrew Cunningham, Alejandro Acosta, Andrew Aitken, Alykhan Tejani, Johannes Totz, Zehan Wang, et al. Photo-realistic single image superresolution using a generative adversarial network. In Proceedings of the IEEE conference on Computer Vision and Pattern Recognition, pp. 4681-4690, 2017.
15. Victor Lempitsky, Andrea Vedaldi, and Dmitry Ulyanov. Deep Image Prior. In IEEE Conference on Computer Vision and Pattern Recognition, pp. 9446-9454, 2018.
16. Peter B Roemer, William A Edelstein, Cecil E
Hayes, Steven P Souza, and Otward M Mueller. The NMR phased array. Magnetic resonance in
medicine, 16(2):192-225, 1990.
Figures
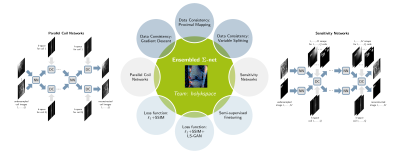
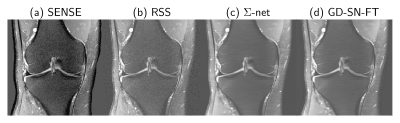
Figure 2: A PDFS@1.5T case from the fastMRI validation set for R=8. (a) Fully-sampled sensitivity-weighted reference used for SN training (b) RSS target for quantitative challenge evaluation (c) ensembled ∑-net (d) semi-supervised finetuning. To match the intensity values of (b), a STL was applied to all SNs. This, however, reduces the quality of our initial results and has no practical relevance.