Purpose

3D multi-slab diffusion-tensor imaging can achieve higher spatial resolution with improved SNR efficiency, therefore being superior to 2D DTI [1]. However, because of non-ideal excitation profile and crosstalk effect, the multi-slab acquisition often leads to slab boundary artifact (SBA) [2,3,4]. Moreover, the off-resonance effect can cause distorted slab profile during excitation, leading to aliasing artifact along slice-encoding direction in the final reconstruction images [6]. Thus, additional correction is required to produce high-quality 3D DTI data. In this work, we proposed to address aforementioned issues associated with multi-slab acquisition using sliding-slab profile encoding (SLIPEN) method, by incorporating additional slab-profile encoding and off-resonance correction into the reconstruction framework.

Methods

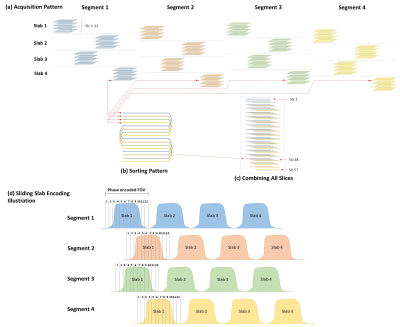
Acquisition Strategy: We have enabled sliding-slab technique [6,7] for acquiring different in-plane segments of 3D multi-slab DTI data with interleaved-EPI readout. To avoid spin history effect, the acquisition of in-plane segment is arranged at outermost loop of entire data acquisition (Fig.1a). Afterward, all in-plane segment data acquired with different slice(kz) encoding from multiple slabs are sorted by slice location, to generate the full 3D image volume (Figs.1b&c). To minimize the crosstalk effect between two adjacent slabs, a gap with 50% of effective slab thickness is used (Fig.1d). The interleaved sliding-slab pattern is also applied to improve the performance of following reconstruction.
Data Reconstruction: The proposed SLIPEN reconstruction method mainly consists of three reconstruction stages, summarized in Fig.2. The preprocessing steps including noise calibration, Nyquist ghost correction, and measurement of inter-shot phase variations are similar as 3D-MUSE method [4]. An additional field map data is acquired to estimate the phase accumulation $$$\Phi_{j}$$$ (for j-th kz encoding) for slab distortion correction.
In the first stage, the direct reconstruction volume image indexed by m, is reconstructed from each segment data $$$d_{m,j,k}$$$ (k represents k-th multi-coil) separately by solving Eq[2] with CG method [9].
$$X_{m} = argmin\left \{ \left \| exp(i\Phi _{j})FC_{k}exp(i\varphi _{m,j})X_{m}-d_{m,j,k} \right \|_{2}^{2} \right \} \qquad[1]$$
where $$$F$$$ represents the Fourier transform, $$$C_{k}$$$ the coil sensitivity, and $$$\varphi_{m,j}$$$ the inter-shot phase variation. Afterward, we use two sliding-summation windows with different kernel sizes [10] to measure the weighting function ($$$W_{m}$$$) of slab profiles for m-th segment data and combine all $$$X_{m}$$$ with weightings to generate the joint reconstruction volume image $$$X$$$.
In the second stage, the high quality joint reconstruction image volume and accurate slab profiles were jointly estimated via an iterative reconstruction algorithm with results from the first stage as initial input. The problem can be reformulated as an optimization problem.
$$\left \{ X,W_{m} \right \} = argmin\left \{ \left \| exp(i\Phi _{j})FC_{k}exp(i\varphi _{m,j})W_{m}X-d_{m,j,k} \right \|_{2}^{2}+\lambda \left \| W_{m}-\overline{W} \right \|_{2}^{2} \right \} \qquad[2]$$
where is the final artifact-free image volume, other notations are kept the same as in Eq[1]. An additional penalty on $$$W$$$ is added to improve the model robustness. $$$\overline{W}$$$ represents the mean of $$$W_{m}$$$, and $$$\lambda$$$ the penalty weighting. The $$$X$$$ and $$$W_{m}$$$ are solved by using alternative gradient descent method.
In-vivo Experiment: Human brain 3D DTI data with 1.3-mm isotropic resolution was acquired from a 3.0T MRI (Philips, Achieva) using proposed acquisition strategy with 4 in-plane segments and 32-channel head coil. Scan parameters: FOV = 208x208x152mm³, number of slabs = 9, kz encoding per slab = 12, effective slab thickness (for RF) = 10.4mm, RF bandwidth = 565Hz, TE1/TE2/TR = 61/112/2000ms, PF factor = 0.71, number of DTI = 6, b = 800s/mm², and scan time = 11.3min.
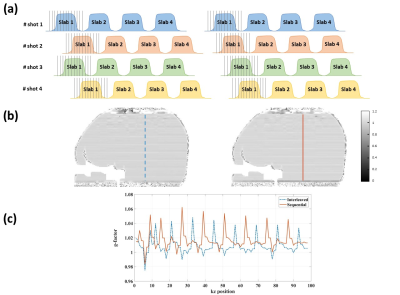
Evaluation: We compared different sliding-slab acquisition patterns to evaluate the reconstruction performance of SLIPEN method by calculating g-factor maps and comparing DTI image quality.

Results

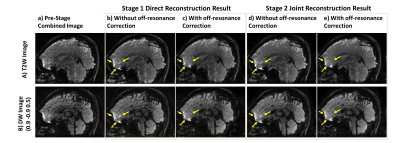
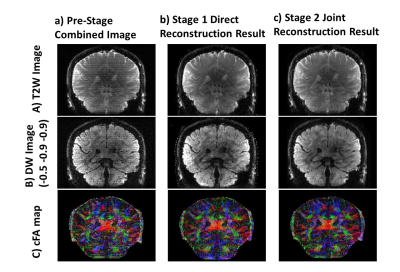
Fig.3&Fig.4 show the reconstructed data by SLIPEN framework at different stages in sagittal and coronal view, respectively. At pre-stage, shown in Fig.3(a)&Fig.4(a), the images suffer from severe SBA and off-resonance effect when directly combining multi-slab data. At first stage, shown in Fig.3(b,c)&Fig.4(b), the SBA can be largely eliminated, but the region with strong off-resonance effect, pointed by yellow arrows in Fig.3(b), still has aliasing artifacts. At the same time, the bright spots near the edges of skull, shown in Fig.4(b), indicate incomplete convergence at first stage. At second stage, shown in Fig.3(d,e)&Fig.4(c), the iterative reconstruction framework can suppress the noise in the middle of joint reconstructed volume data and improve image quality. Fig.5 evaluates two different sliding-slab acquisition patterns in Fig.5(a) by calculating g-factor maps in Fig.5(b). A line profile in Fig.5(c) is chosen for sharpness comparison. Compared to sequential sliding-slab acquisition, interleaved sliding-slab pattern has little effect on g-factor map.

Discussion and Conclusion

In this work, we demonstrated that the proposed SLIPEN method with iterative correction algorithms can effectively produce high-quality 3D DTI data without SBA and distortion along slab direction. A major advantage of SLIPEN is no need to acquire additional data or measure slab profile prior to acquisition of imaging data. Moreover, the proposed joint reconstruction of combined image volume (stage2) and slab profiles outperforms the standard slab profiles estimation method (stage 1). In our preliminary evaluation, the interleaved sliding-slab pattern has little effect on g-factor maps. Further investigation is required to optimize the SNR efficiency associated with sliding-slab pattern. In conclusion, SLIPEN can eliminate SBA in 3D multi-slab DTI, therefore making 3D DTI more practical for neuroscience research.

Acknowledgements

The work was in part supported by grants from Hong Kong Research Grant Council (GRF HKU17138616 and GRF HKU17121517), and Hong Kong Innovation and Technology Commission (ITS/403/18).