INTRODUCTION

Various designs of 3D multi-shot diffusion-weighted imaging (msDWI) with multi-slab acquisition have been proposed to push the spatial resolution of diffusion-tensor imaging (DTI)^1-4. However, the slab-boundary artifacts associated with multi-slab acquisition need to be addressed for achieving high-quality and high-resolution 3D DTI^5,6. In addition, the feasible slab thickness for 3D msDWI is limited by the 2D phase correction assumption for correcting the inter-shot data inconsistency. In light of this, we have proposed the 3D-MUSER technique to improve the feasible slab thickness by enabling 3D phase correction with a 3D single-shot navigator⁷. In our preliminary test, we have successfully obtain single-slab whole brain 3D DTI (i.e., with 100 mm coverage) using 3D-MUSER technique, without suffering from any slab boundary artifact. However, the relatively long scantime and susceptibility to head motion can limit the applications of 3D DTI in neuroscience research, despite high spatial resolution attainable. In this study, we proposed a potential strategy to develop a 3D DTI technique capable of high scan acceleration. A proof-of-concept simulation demonstrated the feasibility of proposed acquisition and reconstruction scheme for producing high-resolution and high-quality 3D DTI data with reduction in scantime.

MATERIAL AND METHOD

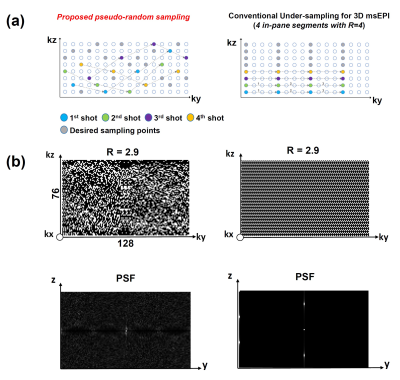
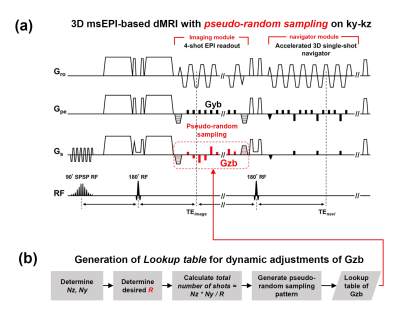
Design of Pulse Sequence
The highly accelerated single-slab 3D msDWI acquisition can be enabled by overcoming the incompatibility between compressed sensing (CS) and 3D multi-shot EPI acquisition. Here, we propose a pseudo-random sampling scheme that is feasible for 3D multi-shot EPI acquisition with high acceleration factor (R). As illustrated in Figure 1a, the acquisition of each k_y segment can be collected with different k_z encodings. From this four in-plane segments example, the proposed sampling scheme can maintain same sampling bandwidth along k_y, and therefore avoiding inconsistent off-resonance effect (Figure 1a). Figure 1b shows examples of uniform sampling and proposed pseudo-random sampling with R=2.9. The proposed pseudo-random sampling scheme can be achieved by modifying the pulse sequence of 3D-MUSER technique, with additional z-gradient blips (G_zb) concurrent with phase-encoding blips (Figure 2a). The acceleration factor and number of shots can be determined firstly, and then a lookup table of k-space trajectory for each shot acquisition is generated and stored (Figure 2b). During data acquisition, the areas of Gzb can be adjusted according to the lookup table in order to achieve pseudo-random sampling after placing all sampled data at appropriate k-space location.

Data Reconstruction
The 3D DTI data acquired with proposed pseudo-random sampling scheme can be reconstructed at hybrid k-space (i.e., x-ky-kz) with the signal model of 3D-MUSER as follow:
$$$ S_{m,k_{yz|j}}(k_{y}.k_{z})=\int_{}^{}\int_{}^{}C_{m}(y,z)\phi_{k_{yz|j}}(y,z)\rho(y,z)e^{-i(yk_{y}+zk_{z})}dydz $$$,
where $$$ S_{m,k_{yz|j}}$$$ is the segment data acquired from m-th coil and j-th shot, $$$ C_{m}(y,z)$$$ the coil sensitivity, $$$\phi_{k_{yz|j}}$$$ the measured 3D phase variation, and $$$\rho(y,z)$$$ the image object. Because the k_y and k_z locations of each segment data (i.e., from j-th shot) are known (from the lookup table), all segment data acquired from all coils can be concatenated and composed an encoding matrix with pseudo-random sampling as $$$\bf S=\widetilde{E}\rho$$$, where $$$\bf \widetilde{E}=F\phi C$$$ ($$$\bf F$$$ is 2D FT operator). Similar to CS reconstruction, the artifact-free image can be solved from a minimization problem of $$$\rho\bf =\min\left\{\parallel\widetilde{E}\rho-S\parallel_{l2}+\lambda_{1}\parallel\rho\parallel_{w}\right\}$$$ using conjugate gradient method.

Hybrid Simulation
A single-slab 3D DTI dataset with 15 diffusion directions was used for simulating the 3D msDWI acquisition with proposed pseudo-random sampling scheme. Two pseudo-random sampling patterns with acceleration factor of 3 and 4 were generated with a predicted hardware constraint for G_zb (i.e., maximum feasible area of G_zb is equal to 6Δk_z). Afterward, the simulated 3D DTI data with two different pseudo-random sampling schemes were reconstructed with proposed model

RESULTS

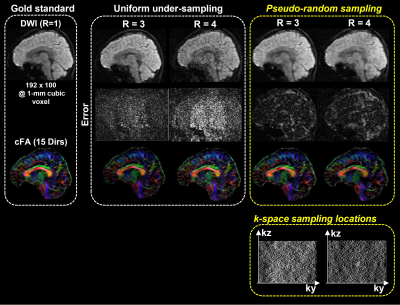
Figure 3 shows the hybrid simulation results of the 3D DTI data accelerated with proposed pseudo-random sampling scheme. The proposed method reveals less reconstruction errors than the data accelerated with conventional uniform under-sampling.

DISCUSSION

Our hybrid simulation demonstrates that the reconstruction performance of proposed pseudo-random sampling is better than conventional uniform sampling, especially at high acceleration factor (e.g., R=4). By analyzing the point-spread-function, pseudo-random sampling scheme transforms the un-aliasing problem to a de-noising problem (Figure 1b). Because of that, a recently developed DM-PCA de-noising can be used to further improve the data quality after image reconstruction⁸. In practice, the pseudo-random sampling pattern is in part limited by the feasible area of G_zb. The hardware performance needs to be considered during the design of proper sampling pattern. If necessary, the echo-spacing can be slightly increased to accommodate the G_zb with larger k_z steps between the acquisition of two adjacent k_y lines. In conclusion, the proposed pseudo-random sampling scheme with 3D-MUSER can enable compressed sensing for 3D DTI acquisition, thereby improve the feasibility of 3D DTI for neuroscience research.

Acknowledgements

The work was in part supported by grants from Hong Kong Research Grant Council (GRF HKU17121517) and Hong Kong Innovation and Technology Commission (ITS/403/18).