0981

Fat-shift suppression in diffusion MRI using rotating phase encoding and localised outlier weighting
Daan Christiaens1,2, Lucilio Cordero-Grande1,3, Jana Hutter3,4, Anthony N Price3,4, Jonathan O'Muircheartaigh1, Katy Vecchiato1, Joseph V Hajnal1,3, and J-Donald Tournier1,3
1Centre for the Developing Brain, School of Biomedical Engineering and Imaging Sciences, King's College London, London, United Kingdom, 2Department of Electrical Engineering (ESAT/PSI), KU Leuven, Leuven, Belgium, 3Biomedical Engineering Department, School of Biomedical Engineering and Imaging Sciences, King's College London, London, United Kingdom, 4Centre for the Developing Brain, King's College London, London, United Kingdom

Synopsis

Diffusion MRI is prone to fat-shift artefacts, especially in accelerated diffusion MRI with higher b-values. Building on the property that the fat signal localisation depends on the phase encoding direction, we propose to suppress fat-shift artefacts in post-processing using localised outlier rejection across 4 different phase encoding directions. To this end, we extend a retrospective diffusion MRI motion correction framework with local outlier weights, defined as a voxel-wise measure of the MR reconstruction residuals. Comparative results in a pediatric brain imaging cohort show that the proposed method reduces fat-shift artefacts in the parenchyma without affecting the reconstruction in uncorrupted regions.

Introduction

Diffusion MRI (dMRI) can probe tissue microstructure in vivo by sensitizing the MRI signal to water self-diffusion1. Most conventional dMRI sequences are based on spin-echo echo-planar imaging (EPI) because its fast readout helps limit sensitivity to bulk motion. However, EPI techniques suffer from fat-shift artefacts due to the relatively low bandwidth in the phase-encoding (PE) direction.

Most common fat suppression methods modify the acquisition sequence, either by a combination of spectrally-selective RF pulses and inversion recovery (SPIR) to null the fat signal longitudinal magnetization2, or by slice-selective gradient reversal (SSGR) to project the fat signal out of plane.3,4 While these techniques work to a certain degree, they are sensitive to static magnetic field (B0) inhomogeneities, especially in multiband imaging and at higher b-values. Further artefact correction is therefore needed, either during MR reconstruction6 or in post-processing.

Here, we propose a new approach based on rotating the phase-encoding direction of each consecutive dMRI encoding/volume. Building on the property that each of the 4 PE-directions projects the fat signal to different spatial positions (Fig.1), the effect of fat-shift artefacts is suppressed through localised outlier rejection in a retrospective motion and distortion correction framework.

Materials and Methods

Data: dMRI data of 15 children aged 8-18 years (7 with epilepsy, 8 controls) were acquired on a Philips 3T Achieva system with a 32-channel adult head coil; resolution 2x2x2mm; MB=3; SENSE=1.5; TE=95ms; TR=3800ms; b=0(8), 300(24), 1000(48), 2600(68) s/mm2; SPIR fat suppression. The PE-direction cycles as LR-RL-PA-AP in consecutive volumes.7 Data were preprocessed with image denoising8 and Gibbs ringing correction9, and a B0 field map was estimated using FSL Topup.10

Local outlier measure: We define voxel-wise inlier weights based on the observation that fat-shift artefacted regions have higher residuals in parallel MRI reconstruction5, captured by the voxel-wise $$$\chi^2$$$-measure across coil channels as shown in Fig.1. Specifically, we adopt a log-normal kernel scaled to 3 times the width of the distribution: $$w_i=\exp\left(-\frac{1}{2}\left(\frac{\log(\chi_i^2)-\hat{\mu}}{3\hat{\sigma}}\right)^2\right)$$ where $$$\hat{\mu}=\mathrm{median}(\log\chi^2)$$$ and $$$\hat{\sigma}=1.48\cdot\mathrm{median}(|\log\chi^2-\hat{\mu}|)$$$. These weights $$$w_i$$$ are calculated for every voxel in the dataset, i.e., as a 4-D image of the same dimensions as the dMRI series, and will be used in during motion correction.

Retrospective motion correction: Subject motion is corrected retrospectively in a dMRI slice-to-volume reconstruction (SVR) framework based on spherical harmonics and a radial decomposition (SHARD).11 This method adopts an inverse problem perspective to find the dMRI signal representation and per-slice subject motion parameters that best explain the measured data, given the acquisition setup and the field map. The overarching cost function is a least-squares fit, weighted using the voxel-wise weights as defined above. Note that the SVR framework also incorporates iterative slice-level outlier reweighting to suppress dropout artefacts. The net weight of every voxel $$$i$$$ is the product of its prior inlier weight $$$w_i$$$ and this dynamically updated weight of the corresponding slice.

Results

A closer look at Fig.1 reveals that the defined voxel-wise weights are close to zero in strongly artefacted regions, effectively excluding these voxels from the SVR. We observed moderate and strong fat-shift artefacts in 5 and 4 datasets respectively.

Fig.2 shows the result of SVR without (top) and with (middle) local outlier weighting in the mean dMRI signal per shell for a representative subject with strong fat-shift artefacts. With outlier weighting, these artefacts are suppressed in the parenchyma and the underlying image contrast is recovered, whilst leaving artefact-free areas unaffected. Similar results were obtained for the other scans.

The fibre orientation distribution (FOD) of the motion corrected output is estimated using multi-tissue constrained spherical deconvolution12 and unsupervised response function estimation13 and is shown in Figs.3-4. The bright fat-signal in high b-value shells strongly affects the estimated fibre orientation distribution (Fig.3), which in turn can have consequences for tractography (Fig.4).

Conclusion

This work has illustrated the benefit of acquiring all 4 PE-directions for recovering dMRI contrast in fat-shift artefacted regions, exploiting the spatially changing localisation. By incorporating local outlier rejection into motion correction, the missing information can be recovered from the other PE-directions. We have furthermore shown that a straightforward, independent metric based on the MR reconstruction error is sufficient to suppress fat-shift artefacts in the parenchyma. Future work can explore closer integration with distortion correction, for which rotating PE-directions have also been shown advantageous.14

Acknowledgements

DC is supported by the Flemish Research Foundation (FWO; grant number 12ZV420N). This work was further supported by ERC grant agreement no. 319456 (dHCP project), by a Sir Henry Dale Fellowship jointly funded by the Wellcome Trust and the Royal Society (Grant Number 206675/Z/17/Z), by the Wellcome EPSRC Centre for Medical Engineering at King’s College London [WT 203148/Z/16/Z], and by the National Institute for Health Research (NIHR) Biomedical Research Centre based at Guy’s and St Thomas’ NHS Foundation Trust and King’s College London. The views expressed are those of the authors and not necessarily those of the NHS, the NIHR or the Department of Health.

References

  1. Le Bihan D, Breton E, Lallemand D, Grenier P, Cabanis E, Laval-Jeantet M. MR imaging of intravoxel incoherent motions: application to diffusion and perfusion in neurologic disorders. Radiology 1986; 161(2):401-7.
  2. Kaldoudi E, Williams SC, Barker GJ, Tofts PS. A chemical shift selective inversion recovery sequence for fat-suppressed MRI: theory and experimental validation. Magn Reson Imaging 1993; 11(3):341-55.
  3. Gomori JM, Holland GA, Grossman RI, Gefter WB, Lenkinski RE. Fat suppression by section‐select gradient reversal on spin‐echo MR imaging. Radiology 1988; 168:493-495.
  4. Nagy Z, Weiskopf N. Efficient fat suppression by slice‐selection gradient reversal in twice‐refocused diffusion encoding. Magn Reson Med 2008; 60(5):1256-1260.
  5. Winkelmann R, Börnert P, Dössel O. Ghost artifact removal using a parallel imaging approach. Magn Reson Med 2005; 54:1002-1009.
  6. Cordero-Grande L, Hutter J, Price AN, Hughes E, Hajnal JV. Goodness of fit factor in SENSE reconstruction: a tool for pseudolesion detection and fat unfolding. 33rd ESMRMB, 458, Vienna, Sep.-Oct. 2016.
  7. Hutter J, Tournier J-D, Price AN, Cordero-Grande L, Hughes EJ, Malik S, Steinweg J, Bastiani M, Sotiropoulos SN, Jbabdi S, Andersson J, Edwards AD, Hajnal JV. Time-efficient and flexible design of optimized multi-shell HARDI diffusion. MRM 2017; 79(3):1276-1292.
  8. Cordero-Grande L, Christiaens D, Hutter J, Price AN, Hajnal JV. Complex diffusion-weighted image estimation via matrix recovery under general noise models. Neuroimage 2019; 200:391-404.
  9. Kellner E, Dhital B, Kiselev V, Reisert M. Gibbs-ringing artifact removal based on local subvoxel-shifts. MRM 2016; 76(5):1574-1581.
  10. Andersson JLR, Skare S, and Ashburner J. How to correct susceptibility distortions in spin-echo echo-planar images: application to diffusion tensor imaging. Neuroimage 2003; 20(2):870-888.
  11. Christiaens D, Cordero-Grande L, Pietsch M, Hutter J, Price AN, Hughes EJ, Vecchiato K, Deprez M, Edwards AD, Hajnal JV, Tournier J-D. Scattered slice SHARD reconstruction for motion correction in multi-shell diffusion MRI of the neonatal brain. arXiv 1905.02996.
  12. Jeurissen B, Tournier J-D, Dhollander T, Connelly A, Sijbers J. Multi-tissue constrained spherical deconvolution for improved analysis of multi-shell diffusion MRI data. NeuroImage 2014; 103:411-426.
  13. Christiaens D, Sunaert S, Suetens P, Maes F. Convexity-constrained and nonnegativity-constrained spherical factorization in diffusion-weighted imaging. NeuroImage 2016; 146:507-517.
  14. Bhushan C, Joshi AA, Leahy RM, Haldar JP. Improved B0-distortion correction in diffusion MRI using interlaced q-space sampling and constrained reconstruction. Magn Reson Med. 2014; 72(5):1218–1232.

Figures

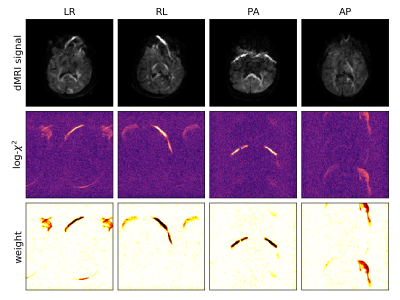
Figure 1: Illustration of the main principles in 4 example image volumes at b-value 2600s/mm2. The top row shows that each phase encoding direction maps the fat signal onto different spatial positions. The middle row shows that the goodness-of-fit in MR reconstruction is sensitive to these fat-shift artefacts. The bottom row shows the derived voxel weight, to be used in the slice-to-volume reconstruction.

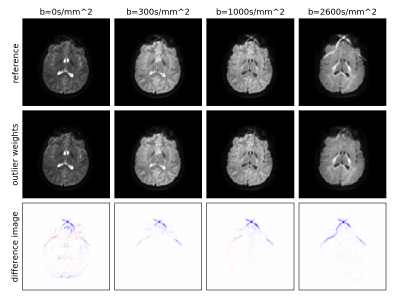
Figure 2: Mean signal per shell (b-value) after motion correction in a dataset strongly affected by a fat-shift artefact, using unit voxel weights (top) and using the proposed local outlier metric (middle; matched intensity scaling). The bottom row shows the difference. We observe successful artefact suppression in the parenchyma, most prominently in the b=2600s/mm2 shell.

Figure 3: Fibre orientation distribution (FOD) in of the resulting reconstruction without (A-C) and with (D-E) local outlier weighting, shown in axial (A,D), sagittal (B,E) and coronal (C,F) slices. The fat-shift artefact, indicated by the arrows, leaves a clear imprint on the FOD when not accounted for, but is effectively suppressed when using local outlier reweighting.

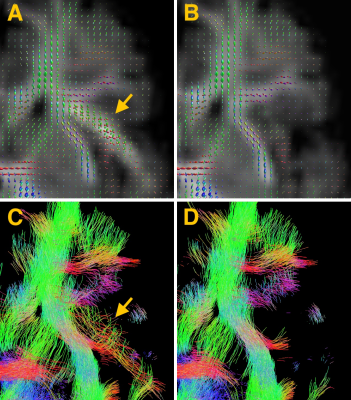
Figure 4: Top: Fibre orientation distribution (FOD) in an axial slice of the frontal lobe, shown for reconstructions without (A) and with (B) local outlier weighting. Bottom: Whole-brain streamline tractography in this region, shown with slab thickness 2mm, again without (C) and with (D) local outlier weights. Image C shows a false positive fibre bundle in the artefacted region, not present when using local outlier weighting.

Proc. Intl. Soc. Mag. Reson. Med. 28 (2020)
0981