Purpose

Diffusion tractography is commonly used to infer the human brain connectome via tracing axonal trajectories¹. Technical difficulties in tracing highly-curved axonal trajectories across white matter-gray matter (WM-GM) boundaries in gyral blades can result in gyral bias. Gyral bias caused by existing tractography algorithms can lead to severe bias in connectivity analysis². Gyral bias can be attributed to the complexity of fiber arrangement in superficial WM underneath the cortical sheet. In this abstract, we demonstrate that a novel tractography method, called active cortex tractography (ACT), can mitigate gyral bias by enabling fiber streamlines to enter the cortex not only into gyral crowns but also sulcal banks, nearly perpendicular to the WM-GM interface.

Methods

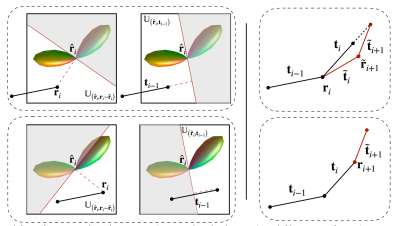
Tractography. Tractography methods typically reconstruct fiber streamlines by successively following local directions using the Euler forward method $$$\mathbf{r}_{i+1} = \mathbf{r}_{i} +\rho \mathbf{t}_i,$$$where the streamline $$$\mathcal{X}=[\mathbf{r}_{0}, \cdots, \mathbf{r}_{n} ]$$$ is estimated using a fixed step size $$$\rho$$$. The forward direction $$$\mathbf{t}_{i}$$$ is typically chosen from the directions that correspond to the local maxima of the fiber orientation distribution function (FODF) in the voxel containing $$$\mathbf{r}_{i}$$$, minimizing the angular deviation with respect to the previous direction $$$\mathbf{t}_{i-1}$$$.
ACT. To estimate subvoxel fiber orientation such as fanning and bending in gyral blades, asymmetric FODFs³ have been employed to improve tractography in gyral blades by explicitly considering subvoxel orientation asymmetry and continuity across neighboring voxels. Let $$$\mathbb{U}_{({\mathbf{r}}, {\mathbf{n}})}$$$ be the voxel subspace defined by the position vector $$${\mathbf{r}}$$$ with the normal vector $$${\mathbf{n}}$$$. Then, with an asymmetrc FODF $$$\mathcal{F}$$$, the temporary forward direction $$$\tilde{\mathbf{t}}_i$$$ can be determined in a voxel subspace $$$\mathbb{U}$$$ (see Fig.1, Left): $$$\tilde{\mathbf{t}}_i = \arg\max_{\mathbf{t}^{*} \in {\mathbb{U}}} \mathcal{F}_{\mathbf{r}_i}(\mathbf{t}^{*}), {\mathbb{U}} := \mathbb{U}_{(\hat{\mathbf{r}}_i, \mathbf{r}_i - \hat{\mathbf{r}}_i)} \cap \mathbb{U}_{(\hat{\mathbf{r}}_i, {\mathbf{t}_{i-1}})}. $$$ Following the tracking streamline, we further adaptively update the forward direction (see Fig. 1, Right) based on the asymmetric FODF, i.e., $$${\mathbf{t}}_i = {\delta}_i\tilde{\mathbf{t}}_i + {\delta}_{i+1}\tilde{\mathbf{t}}_{i+1},$$$ where $$${\delta}_i=\rho\mathcal{F}_{\mathbf{r}_{i}}(\tilde{\mathbf{t}}_i)$$$ and $$${\delta}_{i+1}=\rho\mathcal{F}_{\tilde{\mathbf{r}}_{i+1}}(\tilde{\mathbf{t}}_{i+1})$$$ with a temporary position $$$\tilde{\mathbf{r}}_{i+1}=\mathbf{r}_i+\rho\mathcal{F}_{\mathbf{r}_{i}}(\tilde{\mathbf{t}}_i)\tilde{\mathbf{t}}_i$$$. Then, the next position $$$\mathbf{r}_{i+1}$$$ is updated with the adaptive step size $$$\mathbf{r}_{i+1} = \mathbf{r}_{i} + \rho\mathcal{F}_{\mathbf{r}_{i}}({\mathbf{t}}_i){\mathbf{t}}_i$$$. Moreover, we harness the anatomical information provided by the cortex to guide the tracking of the streamline when it enters the gyral blade and into the cortex. This is achieved by updating the forward direction by $$${\mathbf{t}}_i \leftarrow {\mathbf{t}}_i + \exp(-\|\mathbf{r}_i - {\mathbf{p}_i}\|) \mathbf{v}_i,$$$ where $$${\mathbf{p}_i}$$$ is a vertex on the WM surface with normal vector $$$\mathbf{v}_i$$$, which is chosen such that $$$\{\mathbf{p}_i, \mathbf{v}_i\} = \arg\min _{\mathbf{p},\mathbf{v}} \exp(-\|\mathbf{r}_i - {\mathbf{p}}\|) \arccos(\mathbf{v} \cdot {\mathbf{t}}_i), \mathbf{v} \in \mathbb{V},$$$ and $$$\mathbb{V}$$$ is a field of surface normals. The sign of the normal vector is flipped when the streamline leaves the cortex into the superficial WM: $$$\mathbf{v}_i = \left\{{\begin{array}{cc}{\mathbf{v}_i,}&{~\text{if}~\arccos(\mathbf{v}_i \cdot {\mathbf{t}}_i) \leq \frac{\pi}{2},}\\{-\mathbf{v}_i,}&{~\text{if}~\arccos(\mathbf{v}_i\cdot {\mathbf{t}}_i) > \frac{\pi}{2}}.\end{array}}\right.$$$

Materials

We utilized the diffusion MRI datasets of a macaque brain⁴ and a human brain (from the HCP⁵ ) for validation. The acquisition details of the macaque data and the HCP data can be found in the original papers^{4, 5} . Qualitative and quantitative comparisons were performed with respect to two common algorithms, e.g. deterministic tractography (DT) and iFOD2⁶ , with the same seeding strategies and the same number of streamlines.

Results

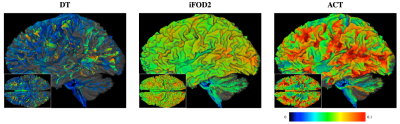
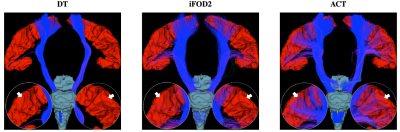
Fig. 2 shows the distribution of average curvatures of streamlines at WM-GM boundary voxels of the macaque brain using WM, GM, and WM-GM boundary seeding. This confirms that ACT consistently improves cortical tractography by tracing highly-curved axonal trajectories across WM-GM boundaries in gyral blades, despite changes in seeding scheme. Fig. 3 shows the distribution of average curvatures of streamlines at WM-GM boundary voxels of the human brain using WM seeding. This confirms that ACT improves cortical tractography by mitigating the effects of gyral bias and allows fiber streamlines at gyral blades to make sharper turns into the cortical GM. We further validated the ACT by tracking the corticospinal tract (CST), which is defined as tracts connecting the postcentral gyri and the brain stem. Seeding is performed in these two regions with the help of FreeSurfer cortical parcellation. Fig. 4 indicates that ACT yields fiber streamlines that cover more of the postcentral gyri (white arrows), indicating better cortical connectivity.

Conclusion

We have presented a tractography method for tracking of high-curvature WM pathways in the gyral blade with cortical prior information to mitigate gyral bias. Our method allows adaptive estimation of forwarding direction in tracking based on asymmetric FODF as well as direction priors at the WM-GM boundary. We showed that, with ACT, fiber streamlines at gyral blades are able to make sharper turns in gyral blades into the cortical gray matter

Acknowledgements

This work was supported in part by NIH grant NS093842.