0969

DeepDTI: Six-direction diffusion tensor MRI using deep learning
Qiyuan Tian1,2, Berkin Bilgic1,2, Qiuyun Fan1,2, Congyu Liao1,2, Chanon Ngamsombat1, Yuxin Hu3, Thomas Witzel1, Kawin Setsompop1,2, Jonathan R. Polimeni1,2, and Susie Y. Huang1,2
1Martinos Center for Biomedical Imaging, Massachusetts General Hospital, Charlestown, MA, United States, 2Department of Radiology, Harvard Medical School, Boston, MA, United States, 3Department of Electrical Engineering, Stanford University, Stanford, CA, United States

Synopsis

Diffusion tensor imaging (DTI) is widely used clinically but typically requires acquiring diffusion-weighted images (DWIs) along many diffusion-encoding directions for robust model fitting, resulting in lengthy acquisitions. Here, we propose a joint denoising and q-space angular super-resolution method called “DeepDTI” achieved using data-driven supervised deep learning that minimizes the data requirement for DTI to the theoretical minimum of one b=0 image and six DWIs. Metrics derived from DeepDTI’s results are equivalent to those obtained from three b=0 and 19 to 26 DWI volumes for different scalar and orientational DTI metrics, and superior to those derived from state-of-the-art denoising methods.

Introduction

Diffusion tensor imaging (DTI) is used for probing tissue microstructure1,2 and for mapping major white matter bundles in the brain. At least 30 diffusion-weighted images (DWIs) acquired along uniformly distributed directions are needed to robustly derive DTI metrics that do not depend on the specific diffusion directions acquired3,4. For DWIs with very low SNR, the number of required DWIs may be far greater than 30. The length of such acquisitions poses a significant barrier to performing high-resolution DTI in routine clinical practice and large-scale research studies.

Previous studies have demonstrated the promise of deep learning in reducing the amount of diffusion data required to generate scalar diffusion metrics5-7. In this work, we propose a physics-informed supervised deep learning technique called “DeepDTI” that minimizes the data requirement for DTI to the theoretical minimum of one b=0 images and six DWIs and enables the generation of scalar and orientational DTI metrics from DWIs sampled along six optimized diffusion-encoding directions.

Methods

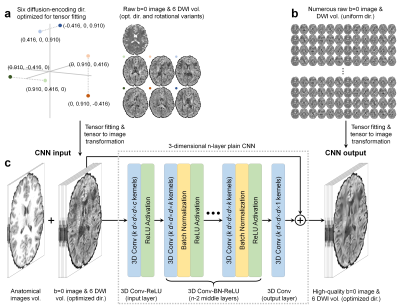
DeepDTI Pipeline. The inputs to DeepDTI are: a single b=0 image, six DWIs sampled along fixed, optimized diffusion-encoding directions (Fig.1a,b), and anatomical (T1- and T2-weighted) images (total of nine input channels). Input DWIs are generated by fitting the tensor model to the input data and inverting the transformation to generate a set of DWIs sampled along six fixed, optimized diffusion-encoding directions extracted from routinely acquired multi-directional, single-shell diffusion MRI data. The diffusion-encoding directions were optimized to minimize the condition number of the diffusion tensor transformation matrix8, hence improving robustness to experimental noise. Many rotational variations of the six optimized diffusion-encoding directions can be chosen, making the method applicable to a range of protocols. For example, from 90 uniform diffusion-encoding directions, ~100 sets of rotational variants can be selected. Anatomical images are included as inputs to delineate boundaries between tissue types and prevent blurring in the fitted results.

The outputs of DeepDTI are: the average of all b=0 images and six ground-truth DWIs (total of seven output channels). The ground-truth DWIs are generated by fitting the tensor model to all available b=0 and DWIs and inverting the transformation to generate a set of DWIs sampled along the six fixed diffusion-encoding directions such that the input and ground-truth DWIs have the same contrast.

A deep 3-dimensional plain CNN9-11 was used to learn the mapping from the input to the residuals between the input and output images (residual learning) (Fig.1d).

HCP Data. Pre-processed diffusion MRI data of 70 subjects (40 for training, 10 for validation, 20 for evaluation) from the Human Connectome Project (HCP) WU-Minn-Oxford Consortium were used12. Diffusion data were acquired at 1.25-mm isotropic resolution along 90 uniformly-sampled diffusion-encoding directions at b=1,000 s/mm2 and 18 interspersed b=0 volumes. For each subject, five sets of one b=0 image and six DWIs along arbitrary rotational variants of the optimized diffusion-encoding directions were selected to obtain input data for DeepDTI. T1-weighted and T2-weighted images were acquired at 0.7-mm isotropic resolution.

Network Implementation. DeepDTI was implemented using the Keras API (https://keras.io/) with a Tensorflow (https://www.tensorflow.org/) backend. Training was performed with 64×64×64 voxel blocks, Adam optimizer, L2 loss using an NVidia V100 GPU for 48 epochs for ~70 hours.

Results

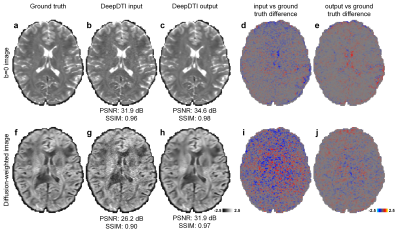
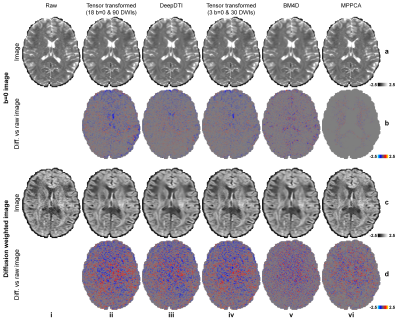
The output DWIs from DeepDTI showed significantly improved image quality and SNR compared to the input DWIs (Fig.2). The output DWIs were similar to the ground-truth DWIs with a high peak SNR (PSNR) of 31.9 dB and high structural similarity index (SSIM) of 0.97 (Fig.2h). The residuals between the output DWI and ground-truth DWIs did not contain anatomical structure (Fig.2e,j).

DeepDTI can be viewed as a denoising method that produces results (Fig.3iii) comparable to results using more data (Fig.3ii, iv) or from state-of-the-art denoising algorithms BM4D13,14 (https://www.cs.tut.fi/~foi/GCF-BM3D/) (Fig.3v) and MPPCA15,16 (“dwidenoise” function in the MRtrix3 software, https://mrtrix.readthedocs.io) (Fig.3vi). Residuals between the DeepDTI-processed DWIs and raw DWIs did not contain anatomical structure (Fig.3, rows b,d, column i).

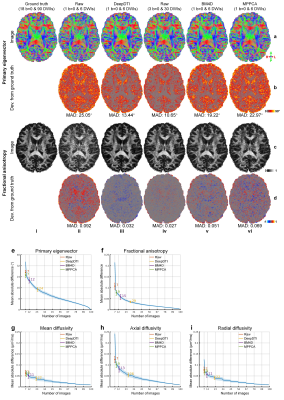
The fractional anisotropy (FA) and primary eigenvector (V1) from DeepDTI recovered detailed anatomical information in deep white matter and cerebral cortex (Fig.4). The V1-encoded FA map from DeepDTI was visually similar and only slightly blurred compared to the map fitted using all 18 b=0 and 90 DWIs.

Deviations of the resultant FA and V1 compared to results fitted using all 18 b=0 and 90 DWIs are shown in (Fig.5a–d) and systematically quantified in the 20 evaluation subjects (Fig.5e–i). The mean absolute deviation (MAD) of V1, FA, mean diffusivity, axial diffusivity and radial diffusivity derived from the DeepDTI outputs was 14.83°±1.51°, 0.036±0.0038, 0.0382±0.0087 mm2/s, 0.055±0.0097 mm2/s, and 0.0413±0.0081 mm2/s, respectively, which were equivalent to the MAD of results from 3 b=0 images and 19, 21, 26, 19, and 23 DWI volumes along uniform directions (Fig.5e–i), achieving 3.1–4.1× acceleration of scan time.

Discussion and Conclusion

DeepDTI performs simultaneous denoising and q-space angular super-resolution by leveraging the data redundancy in the six-dimensional joint k-q space, local and global anatomy and between different MRI contrasts. DeepDTI can also take input DWIs at lower-resolution to generate super-resolution DTI results at higher-resolution, and input DWIs along more than six directions for very noisy data.

Acknowledgements

This work was supported by the NIH (grants P41-EB015896, U01-EB026996, K23-NS096056) and an MGH Claflin Distinguished Scholar Award.

References

[1] Basser, P. J., Mattiello, J. & LeBihan, D. MR diffusion tensor spectroscopy and imaging. Biophysical journal 66, 259-267, doi:10.1016/S0006-3495(94)80775-1 (1994).

[2] Pierpaoli, C., Jezzard, P., Basser, P. J., Barnett, A. & Di Chiro, G. Diffusion tensor MR imaging of the human brain. Radiology 201, 637-648, doi:10.1148/radiology.201.3.8939209 (1996).

[3] Jones, D. K. The effect of gradient sampling schemes on measures derived from diffusion tensor MRI: a Monte Carlo study†. Magnetic Resonance in Medicine 51, 807-815 (2004).

[4] Jones, D. K., Knösche, T. R. & Turner, R. White matter integrity, fiber count, and other fallacies: the do's and don'ts of diffusion MRI. NeuroImage 73, 239-254 (2013).

[5] Li, H. et al. in The Machine Learning (Part II) Workshop of the International Society for Magnetic Resonance in Medicine, Washington, District of Columbia, USA.

[6] Gong, T. et al. in In Proceedings of the 26th Annual Meeting of the International Society for Magnetic Resonance in Medicine (ISMRM), Paris, France. 1653.

[7] Golkov, V. et al. q-Space deep learning: twelve-fold shorter and model-free diffusion MRI scans. IEEE transactions on medical imaging 35, 1344-1351 (2016).

[8] Skare, S., Hedehus, M., Moseley, M. E. & Li, T.-Q. Condition number as a measure of noise performance of diffusion tensor data acquisition schemes with MRI. Journal of Magnetic Resonance 147, 340-352 (2000).

[9] Zhang, K., Zuo, W., Chen, Y., Meng, D. & Zhang, L. Beyond a gaussian denoiser: Residual learning of deep cnn for image denoising. IEEE Transactions on Image Processing 26, 3142-3155 (2017).

[10] Kim, J., Kwon Lee, J. & Mu Lee, K. Accurate image super-resolution using very deep convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 1646-1654 (2016).

[11] Simonyan, K. & Zisserman, A. Very deep convolutional networks for large-scale image recognition. Preprint at: https://arxiv.org/abs/1409.1556 (2014).

[12] Glasser, M. F. et al. The minimal preprocessing pipelines for the Human Connectome Project. NeuroImage 80, 105-124 (2013).

[13] Maggioni, M., Katkovnik, V., Egiazarian, K. & Foi, A. Nonlocal transform-domain filter for volumetric data denoising and reconstruction. IEEE transactions on image processing 22, 119-133 (2012).

[14] Dabov, K., Foi, A., Katkovnik, V. & Egiazarian, K. Image denoising by sparse 3-D transform-domain collaborative filtering. IEEE Transactions on image processing 16, 2080-2095 (2007).

[15] Veraart, J., Fieremans, E. & Novikov, D. S. Diffusion MRI noise mapping using random matrix theory. Magnetic resonance in medicine 76, 1582-1593 (2016).

[16] Veraart, J. et al. Denoising of diffusion MRI using random matrix theory. NeuroImage 142, 394-406 (2016).

Figures

Figure 1. DeepDTI pipeline. DeepDTI adopts a 3-dimensional plain convolutional neural network (CNN) comprised of stacked convolutional filters paired with ReLU activation functions (n=10, k=192, d=3) (d). The CNN input is a single b=0 image and six diffusion-weighted images (DWIs) sampled along optimized diffusion-encoding directions (a, b) as well as anatomical (T1-weighted and T2-weighted) image volumes. The CNN output is the high-quality b=0 image and six DWI volumes transformed from the diffusion tensor fitted using all available b=0 images and DWIs (d).

Figure 2. DeepDTI improves input images. b=0 images (a–f) and diffusion-weighted images (DWIs) (f–j) sampled along one direction of the six optimized diffusion-encoding directions (i.e., [0.91, 0.416, 0]) from the ground truth data (a, f), the input data of DeepDTI (b, g) and the DeepDTI output data, and the residuals between the ground-truth images and DeepDTI input images (d, i) and between the ground truth images and the DeepDTI output images (e, j).

Figure 3. DeepDTI performs image denoising. b=0 image (a) and diffusion-weighted image (DWI) (c) along one of the 90 uniform directions (approximately left-right) from the raw data (i), transformed from the diffusion tensor fitted using all 18 b=0 and 90 DWIs (ii), transformed from the DeepDTI output (iii), transformed from the diffusion tensor fitted using all 3 b=0 and 30 DWIs (iv), denoised by BM4D (v) and MPPCA (vi) as well as their residuals (rows b, d, columns ii-vi) compared to the raw image (rows a, c, column i).

Figure 4. DeepDTI improves estimated DTI metrics. Fractional anisotropy maps color encoded by the primary eigenvector derived from diffusion tensors fitted using all 18 b=0 and 90 diffusion-weighted images (DWIs) (a), raw data consisting of 1 b=0 and 6 DWIs sampled along an optimized set of diffusion-encoding directions from the full data set (b), the same 1 b=0 and 6 DWIs processed by DeepDTI, (c), 3 b=0 and 30 DWIs along uniform directions selected from the full data set (f), and the same raw input data consisting of 1 b=0 and 6 DWIs denoised by BM4D (g) and MPPCA (h).

Figure 5. Error quantification. V1 (a) and FA maps (c) from tensors fitted using 18 b=0 and 90 DWIs (i), raw data consisting of 1 b=0 and 6 DWIs (ii), raw data processed by DeepDTI (iii), 3 b=0 and 30 DWIs along uniform directions from full dataset (iv), raw data denoised by BM4D (v) and MPPCA (vi). For 20 evaluation subjects, the mean absolute deviation in brain tissue compared to the ground truth of DTI metrics from the raw and processed 1 b=0 and 6 DWIs is quantified and compared to results obtained from 7–99 diffusion measurements (e–i, uniform directions, 1 b=0 interleaved for every 10 DWIs).

Proc. Intl. Soc. Mag. Reson. Med. 28 (2020)
0969