0962
Measuring Time-Dependent Diffusion Kurtosis Using the MAGNUS High-Performance Head Gradient1Electrical Engineering, Stanford University, Stanford, CA, United States, 2Radiology, Stanford University, Stanford, CA, United States, 3Hospital for Special Surgery in Manhattan, New York, NY, United States, 4GE Global Research, Niskayuna, NY, United States
Synopsis
In this work, we measure time-dependent effects on diffusion kurtosis estimates in the in vivo human brain over an extended range of b-values(458-2000s/mm2) and frequencies(0-96Hz) using a high-performance head gradient coil on a whole-body 3T MRI.
Introduction
Oscillating gradients concatenate multiple diffusion encodings to maintain diffusion weighting at shorter diffusion times1. Measuring the diffusion characteristics at short effective diffusion times/high oscillating frequencies can be useful for separating the effects of restricted diffusion from heterogeneity in the tissue2, and improving sensitivity to diffusion at smaller and specific length scales. In preclinical studies, oscillating diffusion encoding at high frequency has been shown to improve the delineation of stroke3 and the detection and characterization of tumors4. High slew rates are necessary to utilize the full gradient amplitude at high oscillation frequencies. Therefore, the frequency range available to oscillating gradient encoding is constrained by both the gradient slew rate and amplitude. The requirement for large maximum gradient amplitudes as well as high slew rates makes oscillating gradient encoding at high frequencies and b-values difficult to achieve on conventional whole-body gradient systems. Diffusion kurtosis5 is potentially more sensitive to white matter microstructure changes; oscillating gradient kurtosis measurements are even more difficult to acquire because of the higher b-values needed. In this work, we measure (1)time-dependent diffusion effects and (2)diffusion kurtosis with oscillating gradients in the human brain by maximizing the range of b-values(458-2000s/mm2) and frequencies(0-96Hz) using the MAGNUS high-performance head gradient coil at 3T.Methods
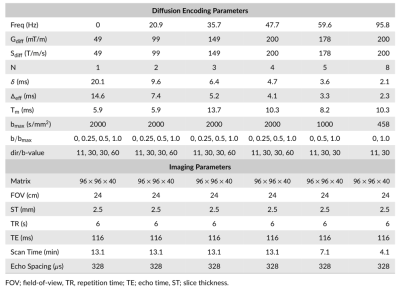
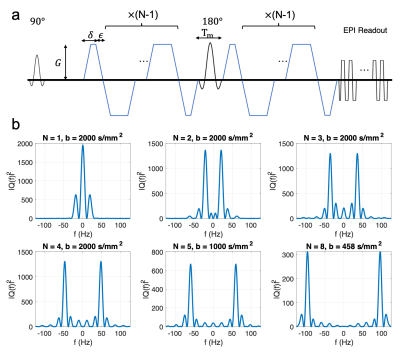
Four subjects were scanned with IRB approval on a 3.0 Tesla whole body magnet (MR750, GE Healthcare) equipped with a head only gradient insert coil6,7(MAGNUS, GE Global Research) and a 32 channel phased array head coil (Nova Medical). The insert gradient coil was operated at 200mT/m and maximum slew rate of 200T/m/s for the diffusion gradients. Scans were performed using a custom cosine-trapezoid oscillating gradient pulse sequence (Fig. 1a) at six oscillation frequencies ranging from 0-96 Hz. The power spectrum of the q-trajectory of the diffusion waveforms were designed with a single peak frequency and matching bandwidths8(Fig. 1b). From 0-48Hz, a three-shell acquisition was used with 30, 30 and 60 orientations uniformly sampled over a half-sphere at 458, 1000, and 2000 s/mm2. An additional 11 non-diffusion weighted images were interspersed evenly through the acquisition to facilitate bulk motion correction. For 60Hz, a two-shell acquisition was used with 30 orientations at 458 s/mm2 and 60 orientations at 1000 s/mm2 and an additional 11 non-diffusion weighted images interspersed evenly through the acquisition. The 96Hz acquisition used 30 directions at a maximum b-value of 458s/mm2. The imaging parameters were TE/TR = 116/6000ms, 96×96×40 matrix, 24×24×10 cm field of view, and 2/3 partial ky. A single-pulsed gradient diffusion scan was also conducted with identical imaging parameters using the three-shell acquisition. The acquisition parameters are summarized in Table 1.Diffusion weighted images were corrected for eddy current distortion, bulk motion and susceptibility distortions9. For each oscillation frequency, the data acquired with b-values less than 1000 s/mm2 were fitted to a diffusion tensor signal model. The three-shell data with an extended b-value range (0-48Hz) were fitted to the diffusion kurtosis model. Whole-brain tractography was performed using mrtrix310, and the result was used to perform automated white matter tract segmentation (AFQ)11. The white matter segmentations were used to compare diffusion tensor and kurtosis parameters across different oscillation frequencies.
Results
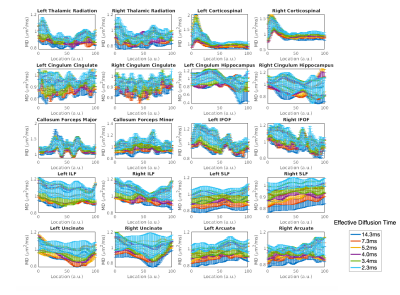
A representative slice from mean kurtosis maps computed from each of the oscillating gradient acquisitions is shown in Figure 2. The diffusion kurtosis parameters displayed a positive correlation with the oscillation frequency across all subjects. The dependence was stronger in kurtosis parameters (MK, RK and AK) than diffusion tensor parameters (MD, RD, and AD). The mean diffusivity across ten different white matter tracts is shown in Figure 3 for each oscillation frequency. An increase of 0-20% in the mean diffusivity was measured between 0Hz and 96Hz. Large increases in mean diffusivity were found in the superior longitudinal fasciculus and portions of the cortical-spinal tracts, while mean diffusivity in the cingulum hippocampus and uncinate displayed little correlation with oscillation frequency. Figure 4 shows plots of the mean kurtosis across ten white matter tracts for oscillation frequencies between 0Hz and 48Hz. Mean kurtosis displayed a strong correlation with oscillation frequency across most white matter tracts. The change in the measured mean kurtosis between 0Hz and 48Hz ranged up to 35% in the cortical-spinal tracts.Discussion
The head-only gradient system enables oscillating diffusion encoding at significantly higher b-values necessary for kurtosis imaging compared to previous in vivo studies on conventional scanners. In theory, the higher b-values improve the sensitivity to restriction at shorter length scales. The achievable b-value was sufficient to measure a strong negative correlation between diffusion kurtosis and oscillation frequency. This behavior is expected since the spins encounter fewer boundaries during the shorter effective diffusion time. The time-dependent behavior of the diffusion signal at high b-values and short effective diffusion times has potential applications and implications for diffusion modeling. While the improved gradient performance may provide access to the biophysical information at shorter length scales, the time-dependent behavior should be accounted for when designing diffusion experiments.Conclusion
Oscillating gradient diffusion encoding on a high-performance gradient system showed a strong dependence of kurtosis measurements on oscillation frequency in white matter with the strongest changes measured within the cortical-spinal tracts.Acknowledgements
Funding provided by an NSF-GRFP, CDMRP W81XWH-16-2-0054, NIH: R01 NS095985, R01 MH111444, R21 MH116484, S10 RR026351, P41 EB015891, GE Healthcare and the Dana Foundation.References
1. Schachter M, Does MD, Anderson AW, Gore JC. Measurements of restricted diffusion using an oscillating gradient spin-echo sequence. J Magn Reson 2000;147(2):232-7.
2. Parsons EC, Does MD, Gore JC. Modified oscillating gradient pulses for direct sampling of the diffusion spectrum suitable for imaging sequences. Magn Reson Imaging 2003;21(3-4):279-85.
3. Wu D, Martin LJ, Northington FJ, Zhang J. Oscillating gradient diffusion MRI reveals unique microstructural information in normal and hypoxia-ischemia injured mouse brains. Magn Reson Med 2014;72(5):1366-74.
4. Reynaud O, Winters KV, Hoang DM, Wadghiri YZ, Novikov DS, Kim SG. Surface-to-volume ratio mapping of tumor microstructure using oscillating gradient diffusion weighted imaging. Magn Reson Med 2016;76(1):237-47.
5. Jensen JH, Helpern JA, Ramani A, Lu H, Kaczynski K. Diffusional kurtosis imaging: the quantification of non-gaussian water diffusion by means of magnetic resonance imaging. Magn Reson Med 2005;53(6):1432-40.
6. Tan ET, Hua Y, Fiveland EW, Vermilyea ME, Piel JE, Park KJ, Ho VB, Foo TKF. Peripheral nerve stimulation limits of a high amplitude and slew rate magnetic field gradient coil for neuroimaging. Magnetic Resonance in Medicine 2020;83(1):352-366.
7. Foo TKF TE, Vermilyea M et al. Highly efficient head-only magnetic field insert gradient coil for achieving simultaneous high gradient amplitude and slew rate at 3.0T (MAGNUS) for brain microstructure imaging. Magnetic Resonance in Medicine 2019.
8. Van AT, Holdsworth SJ, Bammer R. In vivo investigation of restricted diffusion in the human brain with optimized oscillating diffusion gradient encoding. Magn Reson Med 2014;71(1):83-94.
9. Jenkinson M, Beckmann CF, Behrens TE, Woolrich MW, Smith SM. Fsl. Neuroimage 2012;62(2):782-90.
10. Tournier JD, Calamante F, Connelly A. Robust determination of the fibre orientation distribution in diffusion MRI: Non-negativity constrained super-resolved spherical deconvolution. NeuroImage 2007;35(4):1459-1472.
11. Yeatman JD, Dougherty RF, Myall NJ, Wandell BA, Feldman HM. Tract profiles of white matter properties: automating fiber-tract quantification. PLoS One 2012;7(11):e49790.
Figures