Introduction

Tissue movement during diffusion encoding can lead to phase dispersion that is erroneously interpreted as an elevated diffusion coefficient. Although this movement is present in the brain, primarily due to arterial pulsation, it is most relevant in other organs where both cardiac and respiratory motion is prominent. To combat this artifact, diffusion encoding gradient waveforms have been designed to compensate for motion [1,2]. Recently, such waveforms for tensor-valued diffusion encoding [3] were suggested by Lasič et al. [4] based on a symmetric design.
$$$~~~~~$$$In this work we propose a design that uses asymmetric numerically optimized gradient waveforms with nulling of arbitrary moments, and we show that this design improves the encoding efficiency and removes several technical limitations of previous designs.

Methods

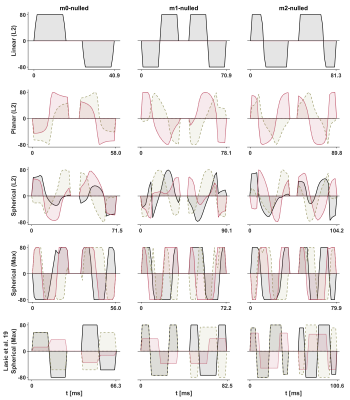
We generate gradient waveforms ($$$\mathbf{g}(t)$$$) by extending the optimization framework by Sjölund et al. [5] to include constraints on the waveform moments; in addition to the constraints on b-tensor shape, gradient amplitude, slew rate, energy consumption, and Maxwell compensation [6]. Moment nulling is achieved by minimizing the magnitude of the moment vector $$$\mathbf{m}$$$ of order $$$n$$$
$$\mathbf{m}_n=\gamma \int_0^{\mathrm{TE}}\mathbf{g}(t)\cdot t^n\mathrm{d}t,$$
to a limit $$$||\mathbf{m}_n||<L_n$$$, where $$$\gamma$$$ is the gyromagnetic ratio and $$$t$$$ is the time. We note that n=1, n=2, n=3 correspond to velocity, acceleration and jerk, respectively. Unlike previous designs [4], the proposed waveforms (i) are not "self-balanced" ($$$||\mathbf{m}_0||\gg0$$$ after refocusing) which removes the need/influence of additional crusher gradients that disturb the motion compensation; (ii) use so called 'M-nulling' so that they can be arbitrarily rotated and distorted by gradient non-linearity without compromising the compensation for concomitant gradient effects [6,7].
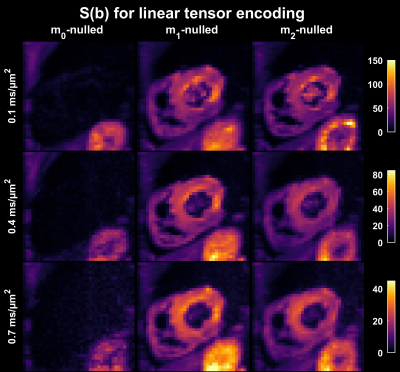
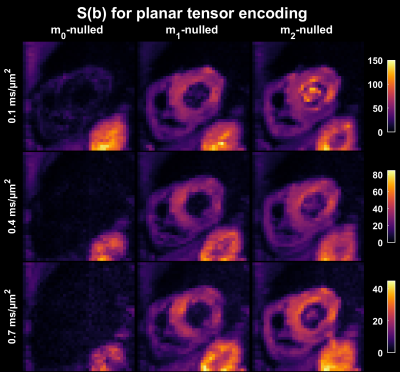
$$$~~~~~$$$To demonstrate the feasibility of this approach, motion compensated waveforms $$$(\mathbf{m}_0,~\mathbf{m}_1,~\mathbf{m}_2)$$$ that yield linear and planar b-tensors [3] were used for diffusion weighted imaging of a healthy heart in vivo. The moment limits were $$$L_0=0,~L_1=10^{-4},~L_2=10^{-4}$$$ in units of sⁿ/m. For comparison, the magnitude of $$$\mathbf{m}_1$$$ and $$$\mathbf{m}_2$$$ for non-compensated waveforms are approximately eight orders of magnitude larger. MRI data were acquired in the heart of a healthy volunteer on a 3 T Prisma (Siemens Healthcare, Erlangen, Germany) using a prototype spin-echo EPI sequence with ZOOM-it excitation, TR = 5 s RR-intervals, TE = [77, 93, 99] ms, partial-Fourier = 6/8, in-plane resolution = 3×3 mm², slice thickness = 8 mm, FOV = 320×118 mm², b = [0.1, 0.4, 0.7] ms/µm² in 6, 10, 15 directions (one repetition). The acquisition was cardiac triggered under free-breathing. The encoding duration was approximately 3 ms longer before than after the refocusing pulse.
$$$~~~~~$$$The impact of motion compensation in the heart was evaluated in terms of the diffusion weighted signal averaged over multiple rotations of planar and linear b-tensor encoding, as well as in terms of the calculated mean diffusivity (MD).
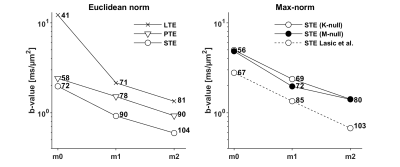
$$$~~~~~$$$The encoding efficiency of waveforms with variable limits on motion encoding was investigated in terms of the maximal b-value achievable for a fix encoding duration, and the necessary encoding time to reach b = 2 ms/µm².

Results

The optimization framework could robustly generate motion compensated gradient waveforms for arbitrary shapes of the b-tensor (Fig. 1) and these could be executed in a cardiac imaging setting. Linear (Fig. 2) and planar b-tensor encoding (Fig. 3) showed a marked improvement from motion compensation; non-compensated waveforms exhibited a massive loss of signal whereas $$$\mathbf{m}_2$$$-nulled waveforms did not. The impact of this on quantification can be appreciated in the MD maps calculated from each set of data (Fig. 4).
$$$~~~~~$$$As expected, the encoding performance was reduced as higher moment nulling was enforced (Fig. 5). However, the novel design outperformed the previous design, shortening the encoding times by up to 23 ms under the given premise. For a larger timing asymmetry, e.g. when ZOOM-it is not used, the advantage becomes even more pronounced (data not shown).

Discussion and conclusions

We have proposed and demonstrated a novel design for motion compensated gradient waveforms for tensor-valued diffusion encoding with significantly improved performance compared to previous designs. The suggested design has several benefits:

• improved performance over previous designs (shorter echo-times and/or higher SNR)
• more flexible, allowing for arbitrary distribution of the encoding time
• automatically account for crushing and therefore achieve more accurate compensation
• ensures Maxwell compensation for arbitrary rotations of the waveforms
• ensures Maxwell compensation even for systems with prominent gradient non-linearity [6]

We expect that this waveform design will improve the feasibility and quality of microstructure imaging based on tensor-valued encoding in organs that require special attention to flow and acceleration compensation, for example cardiac [4] and kidney imaging [8]. Furthermore, the current design can be extended to produce waveforms with combined motion and diffusion sensitization, unlocking an interesting probe of diffusion-motion-correlation experiments. This will be explored in future work.

Acknowledgements

This work was supported by grants from Swedish Research Council (2016-03443). This work was supported by the British Heart Foundation, UK (SI/14/1/30718). We thank David Shelley for performing the MRI scan. We thank Siemens Healthcare (Erlangen, Germany) for access to the pulse sequence programming environment.