0886
Extension of MR-STAT to non-Cartesian and gradient-spoiled sequences1Computational Imaging Group for MR Diagnostics and Therapy, Center for Image Sciences, University Medical Center Utrecht, Utrecht, Netherlands, 2Department of Radiology, Division of Imaging and Oncology, University Medical Center Utrecht, Utrecht, Netherlands, 3Department of Radiotherapy, Division of Imaging & Oncology, University Medical Center Utrecht, Utrecht, Netherlands
Synopsis
MR-STAT is a framework for obtaining multi-parametric quantitative MR maps using data from single short scans. A single large-scale optimization problem is solved in which spatial localisation of signal and estimation of tissue parameters are performed simultaneously. In previous work, MR-STAT was presented using gradient-balanced sequences with linear, Cartesian readouts. To demonstrate the generic nature of the MR-STAT framework and to explore potentially more efficient acquisition schemes, we extend MR-STAT to non-Cartesian gradient trajectories as well as gradient-spoiled sequences. We compare the our results from golden angle radial, gradient-spoiled acquisitions to low-rank ADMM MRF reconstructions on the same data sets.
Introduction
MR-STAT1 is a framework for obtaining multi-parametric quantitative MR maps using data from single short scans. Instead of using the FFT for spatial localisation of signal, followed by parameter estimation on a voxel-per-voxel basis, a single large-scale optimization problem is solved in which spatial localisation of signal and estimation of tissue parameters are performed simultaneously. In previous work,2 MR-STAT was presented using gradient-balanced (e.g. bSSFP/trueFISP) sequences with linear, Cartesian readouts.To demonstrate the generic nature of the MR-STAT framework and to explore potentially more efficient acquisition schemes, we extend MR-STAT to non-Cartesian gradient trajectories as well as gradient-spoiled (e.g. FISP) sequences. First results obtained with radial MR-STAT on simulated data, data from gel phantoms and in-vivo brain data from gradient-spoiled (e.g. FISP) sequences are presented. The results are also compared to (state-of-the-art low-rank ADMM) radial MRF reconstructions3.
Theory
In MR-STAT, parameter maps are obtained by iteratively solving $$\hat{\alpha} = \text{argmin}_{\alpha} \| d - s(\alpha)\|^2$$where $$$d$$$ is the measured data, $$$s$$$ is a Bloch-equation based signal model and $$$\alpha$$$ are the parameter maps concatenated into a single vector. The numerical solution to this large-scale nonlinear optimization problem is obtained with iterative algorithms that require the computation of partial derivatives of the signal $$$s$$$ with respect to the tissue parameters. In the present work the MR-STAT framework was extended to spoiled signal models by incorporating an EPG4 simulator in the forward model. Exact partial derivatives with respect to tissue parameters were computed using automatic differentiation (forward-mode) of the EPG model. The model was also generalized to be able to compute signals and partial derivatives for non-Cartesian gradient encoding schemes.
Methods
Data from a numerical brain phantom was simulated and data from gel phantoms (Eurospin) and an in-vivo brain was acquired on a 3T clinical MR system (Ingenia, Philips, Best, The Netherlands) using the vendors standard 13-channel receive head-coil. For the simulated noise was added to the data such that $$$\|\text{data}\| / \|\text{noise}\| = 100$$$. For all acquisitions, a transient-state gradient-spoiled (FISP) sequence was employed with golden angle radial readouts and flip angles that varied smoothly per TR between 0 and 80 degrees. The sequence was preceded by an inversion pulse. In all cases the total scan time was approximately 10s. The flip angle trains and additional scan parameters are shown in Figure 1.For performing the large-scale nonlinear inversion in MR-STAT, the previously presented matrix-free method Gauss-Newton method was used.2 The MR-STAT reconstructions were implemented on a high-performance computing cluster in the Julia programming language.5
For comparison purposes, the same data sets were also reconstructed using a state-of-the-art MRF reconstruction framework consisting of the low-rank ADMM iterative algorithm,3 which shows superior performance compared to the originally proposed MRF reconstruction scheme.6 For these MRF reconstructions, dictionaries with 100 T1 values and 100 T2 values in logarithmic steps between 0.1s-3s and 0.01s-0.5s, respectively, were generated and compressed to rank 5. The number of ADMM iterations and the ADMM penalty parameter were tuned to give the best results for each data set.
Prior to the reconstructions the data was compressed to a single virtual coil using the SVD. No coil sensitivity information or regularization was utilized in the reconstructions.
Results
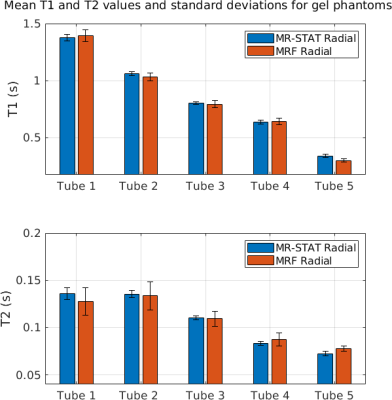
In Figure 2 the reconstructed T1, T2 and PD maps and relative error maps for the numerical brain phantom are shown. Root mean square errors ("RSME") are also computed. It can be seen that for MR-STAT the RMSEs are lower with respect to MRF by approximately a factor two. The reconstruction time for MR-STAT was 2.5 hours using 32 CPUs.In Figure 3 we show T1, T2 and PD maps for the gel phantoms. Mean T1 and T2 values and standard deviations per tube are shown in Figure 4. The mean values show good agreement and the standard deviations for MR-STAT are lower by approximately a factor two compared to MRF. The reconstruction time for MR-STAT was 3 minutes using 32 CPUs.
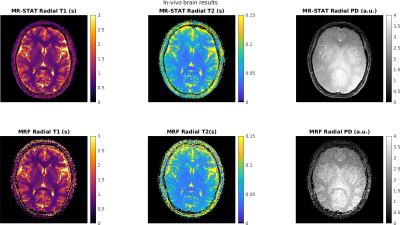
In Figure 5 the T1, T2 and PD maps reconstructed from the in-vivo brain dataset are shown. We observe that the MR-STAT reconstructions suffer less from residual aliasing artefacts. The reconstruction time for MR-STAT was 45 minutes with 100 CPUs.
Discussion
The generic nature of the MR-STAT framework has been demonstrated with the current extension to non-Cartesian and gradient-spoiled sequences. In the MR-STAT reconstructions no FFTs are applied. In particular, no gridding is performed for these radial reconstructions. Instead, the gradient encoding is explicitly modeled. Also, no pre-computed dictionary or low-rank assumptions are used in the MR-STAT reconstructions. This makes MR-STAT flexible with respect to changes in sequence parameters as well as the addition of more tissue parameters into the reconstruction problem. The main downside of MR-STAT is the long reconstruction times, especially compared to MRF which, with the currently used 2D dictionary, take in the order of minutes on a desktop computer.The first results shown in this work suggest that radial MR-STAT is better able to deal with undersampling compared to (state-of-the-art) low-rank ADMM MRF. A more thorough investigation of the differences in reconstruction results is the subject of further studies.
Acknowledgements
This research is funded by the Netherlands Organisation for Scientific Research, domain Applied and Engineering Sciences, Grant #14125.References
[1] Sbrizzi A, van der Heide O, Cloos M, van der Toorn A, Hoogduin H, Luijten PR, van den Berg CAT. Fast quantitative MRI as a nonlineartomography problem. Magnetic Resonance Imaging, 46:56–63, 2018.3.
[2] van der Heide O, Sbrizzi A, Luijten PR, van den Berg CAT. Proc . 26th Sc i. Meet. Int. Soc . Magn. Reson. Med. Paris, 2018:0266.
[3] Assländer J, Cloos MA, Knoll F, Sodickson DK, Hennig J, Lattanzi R. Low rank alternating direction method of multipliers reconstruction forMR fingerprinting. Magnetic Resonance in Medicine, 79(1):83–96, 2018.
[6] Weigel M, Extended phase graphs: Dephasing, RF pulses, and echoes ‐ pure and simple, Journal of Magnetic Resonance Imaging, 41(2):266 -295, 2015.
[5] Bezanson J, Edelman A, Karpinski S, Shah VB. Julia: A fresh approach to numerical computing. CoRR, abs/1411.1607, 2014.
[6] Ma D, Gulani V, Seiberlich N, Liu K, Sunshine JL, Duerk JL, Griswold MA, Magnetic resonance fingerprinting, Nature 495, 187–192.
Figures
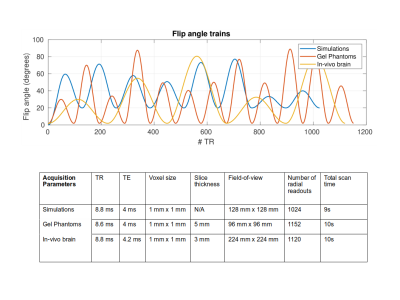
Flip angle trains and acquisition settings used for the numerical brain simulations, the gel phantom scan and the in-vivo brain scan.
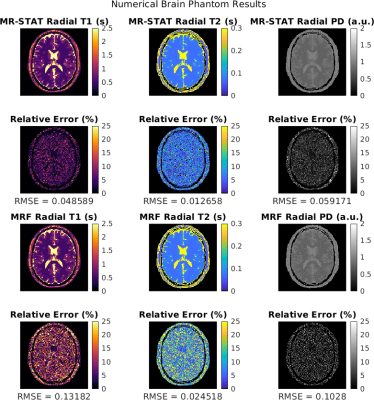
T1, T2 and PD maps reconstructed from the same golden angle radial numerical brain dataset obtained with MR-STAT and low-rank ADMM MRF. Relative percentage error maps are shown in root mean squared errors (RMSE) are computed. We observe that the MR-STAT reconstructions result in lower RMSE values.