0885

Generic Quantitative MRI using Model-Based Reconstruction with the Bloch Equations

Nick Scholand^1,2, Xiaoqing Wang^1,2, Sebastian Rosenzweig^1,2, H. Christian M. Holme^1,2, and Martin Uecker^1,2
¹Department of Interventional and Diagnostic Radiology, University Medical Center, Göttingen, Germany, ²German Centre for Cardiovascular Research, Göttingen, Germany

Synopsis

Conventional quantitative MRI estimates parameters by fitting a known analytical signal model to pixels of images with different contrasts. By combining image reconstruction and the signal model into one non-linear inverse problem, model-based reconstruction methods can estimate the parameters directly from k-space. Avoiding the acquisition and reconstruction of intermediate images they require much less data. Furthermore, they can be directly combined with parallel imaging and compressed sensing, but still rely on analytical models and carefully designed MRI sequences.
Here, we generalize this framework to work with arbitrary sequences using a Runge-Kutta based simulation of spin dynamics.

Introduction

Clinical use of quantitative MRI is usually limited due to the long measurement time. In quantitative MRI the signal is mapped to the relaxation parameters by solving a non-linear inverse problem. Conventional methods rely on an analytical function and solve the inverse problem pixel-wise in the image domain [1-3]. Therefore, a lot of redundant data has to be acquired to obtain fully sampled intermediate images.
Model-based reconstruction schemes combine parameter estimation and image reconstruction into a single inverse problem. Thus, they estimate quantitative parameters directly from k-space data. Conventional methods for model-based reconstruction require analytical signal models that correspond to carefully designed MRI sequences [4-6].
In this work, we developed a generic reconstruction framework based on the Bloch equations, demonstrate its application to different sequences, and present initial in-vivo results.

Theory

We formulate the reconstruction of the parameter maps and the coil sensitivities from k-space data of an arbitrary sequence as a non-linear inverse problem:
$$ \hat{x} = \underset{\boldsymbol{x}}{\textrm{argmin}}\|A(\boldsymbol{x})-\boldsymbol{y}\|_2^2+\alpha\boldsymbol{Q}(\boldsymbol{x_c})+\beta\boldsymbol{R}(\boldsymbol{x_p}), $$
with a smoothness penalty $$$\boldsymbol{Q}$$$ for the coil sensitivities $$$\boldsymbol{x_c}$$$ and a sparsity-based penalty $$$\boldsymbol{R}$$$ for the parameter maps $$$\boldsymbol{x_p}$$$. Thus, the reconstruction combines calibrationless parallel imaging [7], compressed sensing [8] and model-based reconstruction into a single framework. The non-linear inverse problem is solved by the IRGNM-FISTA algorithm [6].
In contrast to previous work [4-6], the signal model is generalized and is now based on the Bloch equations. By specifying the external fields, the model can be adapted to arbitrary MRI sequences. A schematic drawing of the forward operator is presented in Figure 1.
The physical modelling within the forward operator of the Bloch model-based reconstruction is based on a Runge-Kutta [9] oridinary differential equation (ODE) solver applied to the Bloch equations
$$ \frac{\textrm{d}\boldsymbol{M}(\boldsymbol{x_p}, t)}{\textrm{d}t} = \boldsymbol{f}(t, \boldsymbol{M}(\boldsymbol{x_p}, t), \boldsymbol{x_p}). $$
While conventional model-based reconstructions rely on analytical signals to determine the partial derivatives, we exploit a direct sensitivity analysis (DSA) [10] of the Bloch equations to generalize the forward operator to arbitrary sequences and increase the flexibily of the reconstruction. The application of the DSA leads to an ODE for the partial derivatives
$$ \frac{\textrm{d}}{\textrm{d} t}\frac{\partial}{\partial \boldsymbol{x_p}} \boldsymbol{M}(\boldsymbol{x_p}, t) = \frac{\partial}{\partial \boldsymbol{x_p}}\boldsymbol{f}(t, \boldsymbol{M}(\boldsymbol{x_p}, t),\boldsymbol{x_p}), $$
which is solved simultaneously with the signal simulation within the forward operator.

Methods

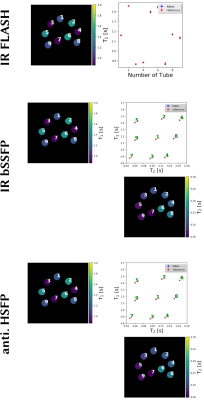
In this proof-of-principle study, we evaluated the Bloch model-based reconstruction using simulations, phantom experiments, and in-vivo experiments.
The simulations were performed pixel-wise in the image domain using an anti-periodic hybrid-state free precession (anti. HSFP) [11], an inversion-recovery bSSFP (IR bSSFP) and an inversion-recovery FLASH (IR FLASH) sequence, respectively. Afterwards, a Fourier transformation is applied to the fully-sampled images to create k-space data. Simulation parameters are listed in Table 1. The reconstructions of the simulated datasets are performed in the $$$T_1$$$-$$$T_2$$$ space for the anti. HSFP and the IR bSSFP sequence. $$$T_2$$$ is kept constant at 100 ms for the IR FLASH reconstruction, because of its low sensitivity to $$$T_2$$$.
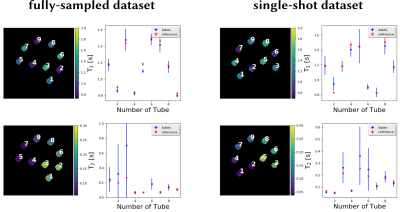
Experimental validations were done using a single-shot IR radial bSSFP dataset acquired within 5 s with the 13th tiny golden angle [12]. A fully-sampled phantom dataset was acquired using the IR radial bSSFP sequence with 191 inversions which resulted in a 45 min acquisition time. Further, gold standard $$$T_1$$$ and $$$T_2$$$ reference data of the phantom were acquired with single-echo spin-echo sequences.
All MRI measurements were performed on a SIEMENS Skyra 3T scanner. The in-vivo brain study is performed on one healthy volunteer with previously obtained informed consent.
All reconstructions are implemented in the BART toolbox [13].

Results and Discussion

Simulation
The estimated parameter maps of the simulated datasets presented in Figure 2 are matching the expected reference values for the multi-parameter mapping techniques. However, the results for the IR FLASH simulation are slightly less accurate which may be due to the use of a constant $$$T_2$$$ map.

Experiments
The developed method is then validated on the phantom data and is compared to the reference measurements as shown in Figure 3. Good mapping accuracy is observed for determining the different relaxation parameter maps for the six tubes with a low $$$T_2$$$ value. The results for the three other tubes are influenced by high-frequency artifacts that increase the standard deviation.
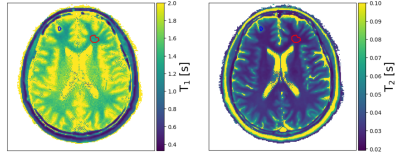
The parameter maps for a human brain are shown in Figure 4. In contrast to the phantom results, the quantitative values do not match the literature values [14,15]. While the $$$T_1$$$ value for gray matter ($$$T_{1,\textrm{gm,est}}$$$=1.79(8) s) is within the range of the expected values ($$$T_{1,\textrm{gm,ref}}$$$=1.331-1.820 s), $$$T_1$$$ of white matter is too high ($$$T_{1,\textrm{wm,est}}$$$=1.30(4) s and $$$T_{1,\textrm{wm,ref}}$$$=0.832-1.084 s), and both $$$T_2$$$ values of white ($$$T_{2,\textrm{wm,est}}$$$=0.026(1) s) and gray matter ($$$T_{2,\textrm{gm,est}}$$$=0.044(2) s) are too low ($$$T_{2,\textrm{wm,ref}}$$$=0.069-0.080 s, $$$T_{2,\textrm{gm,ref}}$$$=0.099-0.110 s). This is likely due to the $$$\alpha/2$$$ magnetization preparation which is sensitive to off-resonance effects [16] and which are not currently accounted for in our forward model. Future work will address this issue.

Conclusion

This work presents a generic sequence-independent reconstruction framework for quantitative MRI. It is directly based on the Bloch Equations which are solved using a generic ODE solver. The gradients of the cost function are obtained using a sensitivity analysis. Initial results on simulations, phantom experiments, and an in-vivo experiment are shown.

Acknowledgements

We thank Jakob Assländer for providing the flipangle file to simulate the anti-periodic HSFP sequence.

References

[1] Crawley AP et al. A comparison of one-shot and recovery methods in T1 imaging. Magn Reson Med. 1988 May;7(1):23-34.

[2] Messroghli DR et al. Modified Look-Locker inversion recovery (MOLLI) for high-resolution T1 mapping of the heart. Magn Reson Med. 2004 Jul;52(1):141-6.

[3] Deoni SC et al.High-resolution T1 and T2 mapping of the brain in a clinically acceptable time with DESPOT1 and DESPOT2. Magn Reson Med. 2005 Jan;53(1):237-41.

[4] Block KT et al. Model-Based Iterative Reconstruction for Radial Fast Spin-Echo MRI. IEEE Trans Med Imag. 2009;28(11). doi: 10.1109/TMI.2009.2023119.

[5] Sumpf T et al. Model-based nonlinear inverse reconstruction for T2 mapping using highly undersampled spin-echo MRI. J Magn Reson Imaging. 2011 Aug;34(2):420-8. doi: 10.1002/jmri.22634.

[6] Wang X et al. Model-based T1 mapping with sparsity constraints using single-shot inversion-recovery radial FLASH. Magn Reson Med. 2018 Feb;79(2):730-740. doi: 10.1002/mrm.26726.

[7] Uecker M et al. Image reconstruction by regularized nonlinear inversion--joint estimation of coil sensitivities and image content. Magn Reson Med. 2008 Sep;60(3):674-82. doi: 10.1002/mrm.21691.

[8] Lustig M et al. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn Reson Med. 2007 Dec;58(6):1182-95.

[9] Dormand J et al. A family of embedded Runge-Kutta formulae. J Comput Appl Math, 1980;6(1).

[10] Lakshmivarahan S et al. Forecast Error Correction using Dynamic Data Assimilation. Springer International Publishing, 2017.

[11] Assländer J et al. Hybrid-state free precession in nuclear magnetic resonance. Commun Phys. 2019 Jun;2(73). doi:10.1038/s42005-019-0174-0.

[12] Wundrak S et al. Golden ratio sparse MRI using tiny golden angles. Magn Reson Med. 2016 Jun;75(6):2372-8. doi: 10.1002/mrm.25831.

[13] Uecker M et al. Software Toolbox and Programming Library for Compressed Sensing and Parallel Imaging. ISMRM Workshop on Data Sampling and Image Reconstruction, Sedona 2013.

[14] Stanisz GJ et al. T1, T2 relaxation and magnetization transfer in tissue at 3T. Magn Reson Med. 2005 Sep;54(3):507-12.

[15] Wansapura JP et al. NMR relaxation times in the human brain at 3.0 tesla. J Magn Reson Imaging. 1999 Apr;9(4):531-8.

[16] Ganter C. Off-resonance effects in the transient response of SSFP sequences. Magn Reson Med. 2004; 52(2):368–375.

Figures

Table 1: Parameters for the numerical simulations and the experiments.

Figure 1: Schematic drawing of the forward operator $$$A=PFCB$$$ chaining the generic Runge-Kutta based simulation $$$B$$$ with a coil operator $$$C$$$ for parallel imaging, a Fourier operator $$$F$$$ as well as a sampling operator $$$P$$$.

Figure 2: Reconstructed $$$T_1$$$ and $$$T_2$$$ maps from simulated data of an IR FLASH, an IR bSSFP and an anti. HSFP sequence. Mean values and standard deviations of selected ROIs are shown in comparison to the true values.

Figure 3: Reconstructed $$$T_1$$$ and $$$T_2$$$ maps of the phantom study for fully-sampled and single-shot IR bSSFP acquisitions. Mean values and standard deviations of selected ROIs are shown in comparison to a single-echo spin-echo reference measurement.

Figure 4: Reconstructed $$$T_1$$$ and $$$T_2$$$ maps of a human brain acquired with a single-shot IR bSSFP sequence in 5 s. The analyzed ROIs for white matter (red) and gray matter (blue) are shown.

Proc. Intl. Soc. Mag. Reson. Med. 28 (2020)

0885