0874
Experimental Comparisons of MRF-FISP Using Optimized Fractional Dictionary and B1 Correction1Shenzhen Institutes of Advanced Technology,Chinese Academy of Sciences, Shenzhen, China, 2Shenzhen College of Advanced Technology, University of Chinese Academy of Sciences, Shenzhen, China, 3State Key Laboratory of Modern Optical Instrumentation, College of Optical Science and Engineering, Zhejiang University, Zhejiang, China, 4Research Center for Medical AI, Shenzhen Institutes of Advanced Technology, Chinese Academy of Sciences, Shenzhen, China
Synopsis
MRF is a time-efficient technique to simultaneously measure of multiple parameters through pattern recognition. The completeness of dictionary to describe the signal evolution process in NMR system is very important to acquire the accurate T1 and T2 values. A new dictionary, generated by using fractional Bloch equations and B1 correction, is proposed to improve the MRF-FISP accuracy. In this work, we compared the accuracy of relaxation values with three dictionary models through phantom and in-vivo experiments. Results illustrated that dictionary generated through fractional Bloch equation with B1 correction is the best to approach T1 and T2 standards.
INTRODUCTION
Magnetic resonance fingerprinting (MRF) is a time-efficient acquisition and reconstruction framework to simultaneously provide multiple parameters including the T1 and T2 maps[1,2]. A challenge in MRF is the accuracy of the resulting multi-parameters. Since the look-up table property in parameter searching, the accuracy of the results is highly correlated to the completeness of the predefined dictionary. Various optimization methods have proposed to improve the accuracy through optimization of sequences design[3,4] and correction from the dictionary generation[5,6]. But all of these corrections are based on the first order Bloch equation for the simple process description. Recently, our group has proposed using fractional calculus to augment the classical relaxation model to include the anomalous temporal behavior of the signal in MRF[7-9] and T1rho mapping[10] applications. The generalization of Bloch equation applied on MRF (FR.-DICT) has been shown the ability to improve the evaluation accuracy of the T1 and T2 maps comparing with the conventional dictionary used in MRF (CONV.-DICT). Since B1 correction has validated to compensate the inhomogeneity of RF excitation in CONV.-DICT[4,5], it is reasonable to further improved parameters accuracy through FR.-DICT with B1 correction. In this work, we proposed to include B1 correction in FR.-DICT and compared the accuracy of relaxation values with three dictionary models through experiments.METHODS
We firstly describe the dictionary models to generate the three dictionaries in this work.Relaxation process in the conventional model (CONV.):
$$M_{z}(t)=M_{z}(0)exp(-\frac{t}{T_{1}})+M_{0}(1-exp(-\frac{t}{T_{1}})),(1a)$$
$$ M_{xy}(t)=M_{xy}(0)exp(-\frac{t}{T_{2}}),(1b)$$
Relaxation process in the fractional model (FR.)[8]:
$$ M_{z}(t)=M_{z}(0)E_{\alpha}(-\frac{t^{\alpha}}{T_{1}'})+M_{0}\cdot\frac{t^{\alpha}}{T_{1}'}E_{\alpha,\alpha+1}(-\frac{t^{\alpha}}{T_{1}'}),(2a)$$
$$ M_{xy}(t)=M_{xy}(0)E_{\beta}(-\frac{t^{\beta}}{T_{2}'}),(2b)$$
where $$$E_{\alpha}$$$ and $$$E_{\beta}$$$ are the single and two-parameter Mittag-Leffler function, respectively.
B1 correction in the dictionary:
$$FAs'=B1(m)\cdot FAs.(3)$$
where FAs’ and FAs are flip angles before and after B1 adjustment. $$$B1(m)$$$is the mth B1 coefficient.
Dictionary design:
The dictionary entries used for MRF matching were generated using Eq.(2) with various {α, β, B1} pairs. The dictionary was generated for a wide range of possible T1 values (range from 100 to 4500 ms), T2 values (range from 10 to 1000 ms), α (alpha) sets to [0.95:0.01:1], β (beta) sets to [0.95:0.01:1], and B1 sets to 0.6:0.02:1.1. As validated in our previous studies, the fractional order model can be simplified to the extension of the conventional model when fractional orders equal to 1. Thus, the three models are: conventional model without B1 correction (CONV.-DICT), conventional model with B1 correction (CONV.+B1-DICT), and fractional model with B1 correction (FR.+B1-DICT).
Data acquisition:
The phantom was scanned on a Siemens 3T Prisma scanner (Siemens Healthcare, Erlangen, Germany) with a 20-channel head–neck receiver array. A FISP based MRF sequence was used in this study. The number of the TR is 1000. A high under-sampled variable-density spiral trajectory was used for data acquisition. Trajectory was rotated by 10 degree at each time instant. NUFFT[11] was used to reconstruct a series of full sample images. The space resolution for the parametric maps was 1×1 mm2 in a field of view (FOV) 220×220 mm2. A self-made phantom and a brain experiments were used for the comparisons of the three dictionaries. Brain scan of one subject was conducted under the approval of the Institutional Review.
RESULTS AND DISCUSSION
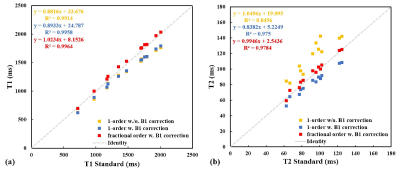
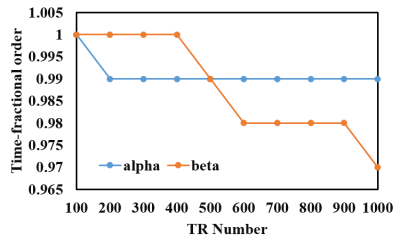
Figure 1 shows the accuracy results of the MRF scan before and after the B1 correction with traditional dictionary model and results with fractional order model after B1 correction. The linear regression and R2 of the results with three methods are also listed in each plot. As shown in the figure, CONV. -DICT model with B1 correction greatly improves the precise of the T2 results compared to the same model without B1 correction. However, CONV.+B1-DICT model reduced T2 values as previously publication founded it in in vivo experiments. Appling the fractional order generation model with the B1 correction, parameters are raised up compared to the CONV.+ B1-DICT model and are generally in good agreement with the results from the reference values, with a concordance correlation coefficient of about 1 for T1 and about 0.98 for T2. The slop of the proposed method to reference values is more near 1 compared to other two models.Figure 2 shows the variation of time-fractional order with the acquisition length. Except at L=100, time-fractional order alpha maintains at 0.99 when TR number increases. Time fractional beta decreases slightly with longer acquisition length. However, only one best fractional order may exist to interpret the most accuracy results, and it can be the conventional one with α=β=1 or fractional ones as Figure 2 shown.
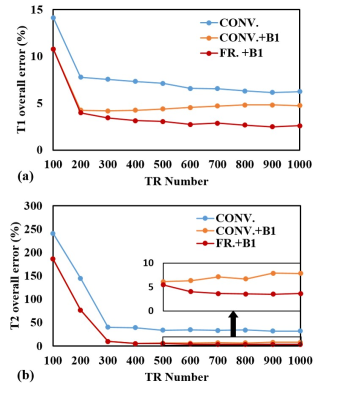
Figure 3 shows the overall errors of T1 and T2 in three models versus the acquisition length. Clearly, the FR.+B1-DICT model outperforms CONV. -DICT and CONV.+B1-DICT models over all the acquisition lengths. T1 and T2 deviations enlarge when acquisition length increases through CONV.+B1-DICT models.
Figure 4 shows T1 and T2 maps of the brain from a volunteer. T2 values are highly improved to show details of the white matter and the gray matter in the brain using the dictionary generated by the FR.+B1-DICT model.
CONCLUSION
Fractional Bloch equation is a flexible tool to describe the signal evolution. The fractional model with B1 correction in the dictionary showed the most identity with the T1 and T2 standards compared to the two conventional models.Acknowledgements
Some of the work was partially supported by the National Natural Science Foundation of China (81801691, 61871373, 81729003, and 61471350), the State Key Program of National Natural Science Foundation of China (Grant No. 81830056), the Natural Science Foundation of Guangdong Province (2018A0303130132), the Strategic Priority Research Program of Chinese Academy of Sciences (XDB25000000), the Shenzhen Peacock Plan Team Program (KQTD20180413181834876), the Shenzhen Key Laboratory of Ultrasound Imaging and Therapy (ZDSYS20180206180631473), and the Sanming Project of Medicine in Shenzhen (SZSM201812005).References
1. D. Ma, V. Gulani, et al., “Magnetic Resonance Fingerprinting,” Nature, vol. 495, pp.187-192, 2013.
2. C. Liao, B. B, et al., “3D MR fingerprinting with accelerated stack-of-spirals and hybrid sliding-window and GRAPPA reconstruction” Neuroimage, vol 162, pp. 13-22, 2017.
3. B. Zhao et al., "Optimal Experiment Design for Magnetic Resonance Fingerprinting: Cramér-Rao Bound Meets Spin Dynamics," in IEEE Transactions on Medical Imaging. doi: 10.1109/TMI.2018.2873704
4. J. Assländer, S.J. Glaser, J. Hennig, “Pseudo steady-state free precession for MR-fingerprinting,” Magn. Reson. Med., vol. 77, pp. 1151–1161, 2017.
5. D. Ma, S. Coppo, Y. et al., “Slice profile and B1 corrections in 2D magnetic resonance fingerprinting,” Magn. Reson. Med., vol. 78, pp. 1781-1789, 2017.
6. Y. Jiang, D. Ma, et al., “MR fingerprinting using fast imaging with steady state precession (FISP) with spiral readout,” Magn. Reson. Med., vol. 74, pp. 1621–1631, 2015.
7. H. Wang, L. Ying, et al., “MRF-FrM: A Preliminary Study on Improving Magnetic Resonance Fingerprinting Using Fractional-order Models”. Proc. 26th Annual Meeting of ISMRM, Paris, France, 2018.
8. L. Zou, H. Wang, et al., “Experimental Validation of Augmented Fractional MR Fingerprinting”. Proc. 27th Annual Meeting of ISMRM, Montréal, Canada, 2019.
9. H. Wang, L. Zou, et al., “Application of Time-Fractional Order Bloch Equation in Magnetic Resonance Fingerprinting”. In: Proc 16th IEEE International Symposium on Biomedical Imaging (ISBI), Venice, Italy, 2019; pp. 1704-1707
10. L. Zou, H. Wang, et al., “T1rho Fractional-order Relaxation of Human Articular Cartilage, ” In: Proc 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Berlin, Germany, 2019, pp. 4496-4499.
11. J.A Fessler, B.P. Sutton, “Nonuniform fast fourier transforms using minmax interpolation,” IEEE Trans. Signal Process, vol. 51, pp. 560–574, 2003.
Figures