0855
Anatomically informed multi-level fiber tractography for improved sensitivity of white matter bundle reconstruction in diffusion MRI
Andrey Zhylka1, Alexander Leemans2, Josien Pluim1, and Alberto De Luca2
1Biomedical Engineering, Eindhoven University of Technology, Eindhoven, Netherlands, 2Image Sciences Institute, University Medical Center Utrecht, Utrecht, Netherlands
1Biomedical Engineering, Eindhoven University of Technology, Eindhoven, Netherlands, 2Image Sciences Institute, University Medical Center Utrecht, Utrecht, Netherlands
Synopsis
Neurosurgery planning is an important application of fiber tractography which requires the results to be consistent and accurate. Deterministic tractography methods are generally characterized by high specificity and limited sensitivity, whereas the opposite typically holds for probabilistic methods. Here, we propose a multi-level fiber tractography strategy that takes fiber branching into account and incorporates an anatomical prior to provide a balance between true and false positive reconstructions. We evaluated our approach on the MASSIVE dataset and compared its performance to the existing state of art.
Introduction
Fiber tractography (FT) with diffusion MRI is a powerful tool for neurosurgery planning as it can reconstruct brain pathways in vivo and noninvasively1. However, it is challenging to obtain a reliable and consistent reconstruction of fiber trajectories2. In particular, probabilistic FT approaches tend to produce more false positive reconstructions than deterministic ones, while deterministic approaches typically produce more false negative pathways. Additionally, neither of the approaches addresses the notion of fiber bundles taking very sharp turns. Moreover, given the angular constraints and resolution that is too coarse for such purpose, branching pathways are quite likely to be pruned leading to an increased false negative rate3. We developed a novel way to reconstruct fiber bundles as multi-level structures, where each consecutive level is a set of pathways branching from the previous one. We investigate whether this strategy in combination with the prior knowledge of the location of seed and target regions of interest (ROI) can improve the sensitivity of the reconstructions, while maintaining properties of deterministic FT.Methods
The proposed strategy was implemented for tractography methods based on constrained spherical deconvolution4 (CSD). It iteratively complements the results with the new levels of branches (Figure 1). At each iteration CSD-based deterministic tractography is performed as the first step (with an angular-deviation threshold of 45° and a fiber orientation distribution (FOD) threshold of 0.1). Secondly, points along a pathway with unused crossing directions are used as new seed points, and the unprocessed FOD peaks as initial directions. This procedure runs either for a pre-defined number of iterations or until a convergence criterion is met. Finally, using prior anatomical knowledge of the tract topology, a terminal ROI is defined to select the pathways that are to remain.The MASSIVE5 dataset was used with isotropic voxel resolution of 2.5mm. The acquisition consisted of 430 volumes at b = 0s/mm2, 250 volumes at b = 500 s/mm2, 500 volumes at 1000s/mm2, 2000s/mm2 and 3000s/mm2 each, 600 volumes at 4000s/mm2. The data was corrected for signal drift, motion and Eddy current using ExploreDTI6. Target areas were selected from the cortical parcellation obtained with FreeSurfer7. Subsequently, the fiber orientation distributions were estimated with multi-shell CSD8.
To evaluate the performances of the proposed method, we reconstructed the corticospinal tract (CST) by selecting the precentral and paracentral gyri as target regions, while seeding below the internal capsule. Each seed voxel was subsampled evenly on 3x3 grid at single slice level. The results of the proposed procedure were compared to those obtained with CSD-based deterministic FT and probabilistic FT given identical tracking parameters and conditions. Probabilistic FT was performed with iFOD29. Pathway coherence was analyzed using TSNE10 as well as functional topology preservation for both algorithms. Generalizability of the method was tested on the cingulum bundle in comparison to deterministic CSD-based FT. For this case, the target region was chosen based on the WMQL-like11 cingulum query, including only the regions containing endpoints of the bundle. The seed ROI for the cingulum was placed on the edge of Brodmann areas 23 and 24.
Results
Figure 2 compares the proposed approach to conventional CSD-based tractography for a left branch of the CST. As compared to CSD, our method provides a more extensive reconstruction of the CST, including branches that constitute more than a half of the well-known “fanning” of the tract into the motor cortex. The iFOD2 algorithm can also reconstruct the CST branches and provides tracts with a good coverage of the motor cortex (Figure 3). However, our approach allows reconstruction of pathways with higher coherence, as supported by the TSNE clustering shown in Figure 3. This aspect is also represented in better preservation of functional topology by the proposed approach, which is shown in Figure 4. Improved tractography results were also obtained for the case of cingulum delineation. Figure 5 compares the cingulum tracking results obtained with our method to those of deterministic fiber tractography from the same seed point regions. The bundle obtained with the proposed approach additionally captures pathways going to the superior lobes in the anterior and posterior parts, whereas deterministic FT reconstructs a more limited part of the bundle.Discussion
In this work, we have shown that the proposed approach is capable of reconstructing complex fiber bundles, such as the corticospinal tract and the cingulum, with improvement in false-negative rate while maintaining properties of deterministic tractography. The produced pathways are more coherent than those produced by probabilistic FT, which are characterized by higher tortuosity and an erratic nature. Consequently, our approach preserves functional topology better than iFOD2. The accuracy of our approach is dependent on the terminal region, which should be defined carefully. An adequate seeding area and a sufficient seed density are also important for an accurate reconstruction. Sparse seeding might lead to a deficit of the expected branching structures in complex cases.Conclusion
We developed a novel way to perform FT by reconstructing multi-level structures that integrates the orientations with a higher angular deviation and that incorporates prior knowledge of fiber tract anatomy. In doing so, we obtain a more complete representation of brain pathways.Acknowledgements
This project has received funding from the European Union's Horizon 2020 research and innovation program under the Marie Sklodowska-Curie grant agreement No 765148.References
- Jeurissen B., Descoteaux M., Mori S., Leemans A. Diffusion MRI tractography of the brain. NMR Biomed 32(4) (2019) e3785.
- Maier-Hein K. et al. The challenge of mapping the human connectome based on diffusion tractography, Nature Communications 8 (1) (2017) 1349.
- Mortazavi F., Oblak A. L., Morrison W. Z., Schmachmann J. D., Stanley H. E., Wedeen V. J., Rosene D. L. Geometric navigation of axons in a cerebral pathway: comparing dMRI with tract tracing and immunohistochemistry. Cerebral Cortex 28(4) (2018) 1219-1232.
- Jeurissen B., Leemans A., Jones D. K., Tournier J.-D., Sijbers J. Probabilistic fiber tracking using the residual bootstrap with constrained spherical deconvolution, Hum Brain Mapp 32 (3) (2011) 461–479.
- Froeling M., Tax C. M., Vos S. B., Luijten P. R., Leemans A. MASSIVE brain dataset: Multiple acquisitions for standardization of structural imaging validation and evaluation, Magn Reson in Med 77 (5) (2017) 1797–1809.
- Leemans, A., Jeurissen, B., Sijbers, J., Jones, D. K. ExploreDTI: a graphical toolbox for processing, analyzing, and visualizing diffusion MR data. ISMRM; 3537 (2009).
- Fischl B. FreeSurfer, NeuroImage 62 (2) (2012) 774–781.
- Jeurissen B., Tournier J.-D., Dhollander T., Connelly A., Sijbers J. Multi-tissue constrained spherical deconvolution for improved analysis of multi-shell diffusion MRI data, NeuroImage 103 (2014) 411–426.
- Tournier J.-D., Calamante F., Connelly A. Improved probabilistic streamlines tractography by 2nd order integration over fiber orientation distributions, ISMSRM; 1670 (2010).
- Oliveira F.H.M., Machado A.R.P., Andrade A.O. On the Use of t-Distributed Stochastic Neighbor Embedding for Data Visualization and Classification of Individuals with Parkinson's Disease. Comput Math Methods Med 8019232 (2018).
- Wassermann D., Makris N., Rathi Y., Shenton M., Kikinis R., Kubicki M., Westin C.F. The white matter query language: a novel approach for describing human white matter anatomy. Brain Struct and Func 221 (9) (2016) 4705-4721.
Figures
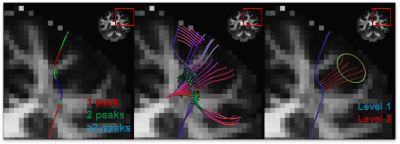
Figure 1. Algorithm pipeline. The tracts produced by
CSD tractography include points corresponding to multiple FOD peaks, which are
ignored (left). Using these points as seeds with unused peaks as initial locations
another iteration of CSD tracking is performed to obtain a new level of the
result (middle). On the last stage only the tracts that enter a predefined target
region remain (right).
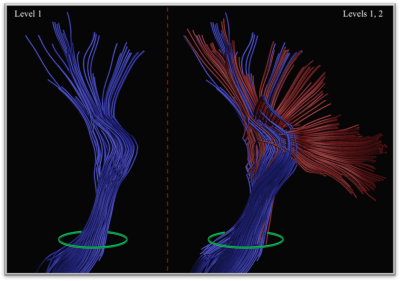
Figure 2.
CSD-based deterministic streamline
propagation approach is only capable of reconstructing a subset of CST pathways
(left). On the other hand, the proposed procedure unleashes potential branching
pathways that constitute more than a half of the CST “fan” (right), while
starting tractography from the same seed region (green circle). In both cases
only the pathways reaching the motor cortex are shown.
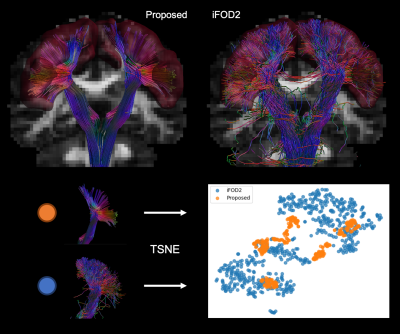
Figure 3. Reconstruction
of corticospinal bundle with the proposed approach and iFOD2 algorithm. Both
results show a good coverage of the brain motor cortex (red surface). The
pathways generated with our algorithm are more coherent: closely grouped
together by TSNE clustering (where each point is a single pathway). The output
of the probabilistic tracking is characterized by higher tortuosity: very sparse
distribution of pathways in the embedding space.
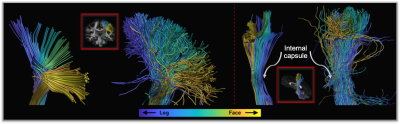
Figure 4.
Pathways are color-coded according to the location of their endpoints in gray
matter. In case functional topology is preserved, the order of colors is
maintained in the internal capsule. Functional topology
of the pathways produced by our approach is more consistent than that observed
in the results of iFOD2 as extra deviation is not introduced during tract
propagation.
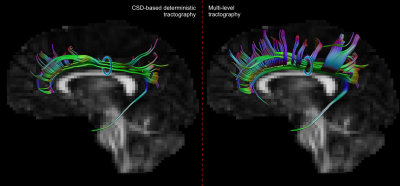
Figure 5.
Comparison of cingulum reconstruction performed from the same seed region (blue
circle). The proposed strategy results in an improved reconstruction of “fannings”
in the anterior and posterior parts of the cingulum that are not captured by
conventional CSD-based streamline tractography.