0846

Characterizing the fine microstructure of cerebellar and cerebral cortex non-invasively with metabolite diffusion-weighted MRS

Marco Palombo¹, Cecile Gallea^2,3, Guglielmo Genovese^3,4, Stephane Lehericy^2,3, and Francesca Branzoli^3,4
¹Centre for Medical Image Computing, Department of Computer Science, University College London, London, United Kingdom, ²Team "Movement Investigations and Therapeutics", Brain and Spine Institute - ICM, Paris, France, ³INSERM U 1127, CNRS UMR 7225, Sorbonne University, Paris, France, ⁴Brain and Spine Institute - ICM, Centre for NeuroImaging Research - CENIR, Paris, France

Synopsis

Diffusion-weighted magnetic resonance spectroscopy (DW-MRS) performed at ultra-high b-values enables the quantification of fine cell microstructural features such as dendritic spine density. Here, we measured in-vivo the diffusion of total N-acetyl-aspartate (tNAA) and choline compounds (tCho) in the human cerebellar and cerebral cortex at 3 T, up to a b-value of 24 ms/μm². We used biophysical modelling and numerical simulations to interpret the metabolite signal attenuation with the b-value. The diffusion of tNAA, a mostly neuronal metabolite, is compatible with a larger presence of spines and highly restricting granular cell soma in cerebellar compared to cerebral cortex.

Introduction

This work aims at characterizing fine microstructural features of cerebellar and cerebral cortex non-invasively through diffusion-weighted spectroscopy (DW-MRS).

The cerebellar cortex comprises granule and Purkinje cells, which present two microstructural features different from the cells of the cerebral cortex. Granule cells have cell bodies, namely soma, of small radius R_soma~3 µm, while Purkinje cells have complex dendritic trees with high spine density ρ_spine>~2 spines/μm^1,2. In contrast, the cerebral cortex is mostly characterized by pyramidal cells with bigger R_soma>~5 µm and lower ρ_spine<~1 spines/μm³, and less abundant stellate/granule cells with smaller soma.

Currently, this structural complexity can be quantified in post-mortem brain using invasive techniques. These measurements have shown that fine morphological features as ρ_spine play an important role for synapse development/plasticity in healthy brain and diseases like autism⁴, essential tremor², dementia⁵. However, there is still an unmet need for non-invasive techniques enabling the in-vivo quantification of such fine morphological features.

DW-MRS is a non-invasive technique able to quantify the complexity of cell morphologies with higher specificity than diffusion-weighted MRI^6-16. Here, we show in-vivo DW-MRS data of the mostly neuronal metabolite N-acetyl-aspartate (tNAA) and the glial choline compounds (tCho)^10,17,18 at ultra-high b-values in human cerebellar and cerebral cortex. Using biophysical and computational modelling, we provide evidence supporting DW-MRS as a potential method to quantify disease-related changes in fine cell microstructures like rspine.

Methods

DW-MRS acquisition/processing. DW-MRS data were acquired in 4 healthy subjects using a DW-semi-LASER¹⁹(Fig.1-C) (TE/TR=125 ms/3 cardiac-cycles) at 3T (Siemens/PRISMA). Volumes-of-interest (VOI) were placed in the cerebellum (15x16x22 mm³) and in the posterior cingulate cortex (PCC, 20x20x20 mm³) (Fig.1-A,B). Diffusion weighting was applied in 4 tetrahedral directions with diffusion-time=62.5 ms and b-values=[0,0.9,3.8,8.6,15.4,24] ms/μm² (24 averages). Unsuppressed-water data were acquired for eddy-current corrections. At each b-value, frequency/phase corrections were performed on single spectra, then averaged (Fig.1-D) before quantification using LCModel²⁰. Signal amplitudes at each b were direction-averaged and analysed.

Data analysis. To characterize metabolite diffusion, we used a model inspired by^7,21-23: the DW-MRS signal from a macroscopic voxel results from metabolite protons diffusing in randomly oriented infinitely-long cylinders of diameter d, with apparent intracellular diffusivity D(D₀,β,b)=D₀(1-βD₀b), where D₀ is the metabolite intracellular diffusivity, and β a parameter similar to kurtosis introduced to account for non-Gaussian diffusion due to the presence of hindering/restricting intracellular structures^21,22. Therefore:

$$S(b)/S(0)=S_{cylinder}[D(D_0,\beta,b),d,b],[1] $$

where S_cylinder is given by Gaussian-phase approximation²⁴.
To estimate D₀, d and β associated with glial and neuronal compartments, we fitted Eq.[1] to the measured tCho and tNAA DW-MRS signals as functions of b-value.
Our working-hypothesis is that, given a root-mean-squared-displacement~6 μm for the diffusion time of our experiments, the cellular structures that may induce non-Gaussian effects are dendritic spines and/or soma. Other relevant features, like cell fibres’ undulation, curvature and branching occur on length scales ~10-100 μm, and should have lower impact, at least for neurons (hence tNAA). For smaller glial structures (hence tCho), these other features may contribute significantly.

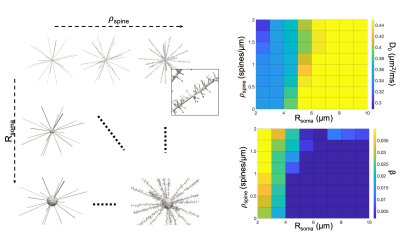
Simulations. To support our working-hypothesis, we compared tNAA and tCho experimental data with Monte-Carlo simulations. We used the advanced computational models from²⁵ and CAMINO²⁶ to investigate the effect of different combination of ρ_spine=[0–2] spines/μm and R_soma=[2–10] μm on the diffusion of 10⁴ particles with D₀=0.45 µm²/ms and cell fibre’s d=1 μm (time-step=25 μs). From spin trajectories, the diffusion-weighted MR signal was computed by phase-accumulation using the experimental protocol and analysed using Eq.[1].

Results

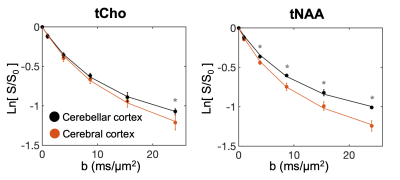
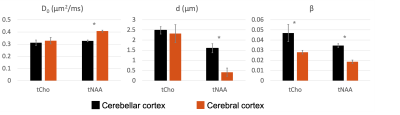
Fig.1-D shows DW spectra acquired from each VOI in one subject. We found a stronger signal attenuation (Fig.2) in the cerebral than in the cerebellar cortex for both metabolites, but significant only for tNAA.

Fig.3 shows the results of our biophysical model fitting. In cerebellar compared to cerebral cortex, we estimated significantly lower D₀ (P<0.001) and larger d (P<0.001) for tNAA and larger β (P<0.001) values for tNAA and tCho (paired two-tail t-test).

Fig.4 shows the simulated computational models and the predicted dependence of D₀ and β on R_soma and ρ_spine. We found that the combinations [ρ_spine~0.8 spines/μm,R_soma~6 µm] and [ρ_spine~2 spines/μm,R_soma~3 μm] can explain the estimated D₀ and β values for tNAA in cerebral and cerebellar cortex, respectively.

Discussion and Conclusion

Our findings suggest that the non-gaussian diffusion of tNAA may be a marker of neuronal ρ_spine. Indeed, estimated D₀ and β values for tNAA data are compatible with the larger ρ_spine and highly restricting granular soma in cerebellar compared to cerebral cortex. Furthermore, comparison with simulations suggests R_somacompatible with cerebral pyramidal and cerebellar granule cells, and typical ρ_spine of cerebral pyramidal³ and cerebellar Purkinje^1,2 cells. Noticeably, we also measured larger β values for tCho in cerebellar compared to cerebral cortex, which could be due to the presence of highly-arborized Bergmann glia²⁷, specifically cerebellar. Also, estimated tNAA and tCho β values agree with other recent estimates of non-gaussianity in cerebral cortex²⁸.

Future study will aim at addressing several limitations of this work, from more simulations and histological validation to sensitivity analysis to further support DW-MRS of tNAA at high b-value as non-invasive method to estimate ρ_spine indices in-vivo in human.

Potential for clinical applications are many and important, from early diagnosis to informed treatment planning for diseases like essential tremor², whose hallmarks are indeed ρ_spine changes in cerebellum.

Acknowledgements

This project has received funding d from Engineering and Physical Sciences Research Council (EPSRC EP/N018702/1); FB and CG acknowledge support from the programs 'Institut des neurosciences translationnelle' ANR-10-IAIHU-06 and 'Infrastructure d’avenir en Biologie Santé' ANR-11-INBS-0006. The authors would like to thank Dr. Edward J. Auerbach and Dr. Małgorzata Marjańska for providing us the DW-MRS sequence for the Siemens platform.

References

1. Hoxha E, et al. (2017) Motor Deficits and Cerebellar Atrophy in Elovl5 Knock Out Mice. Front Cell Neurosci11:343.

2. Louis ED, et al. (2014) Reduced Purkinje cell dendritic arborization and loss of dendritic spines in essential tremor. Brain 137(Pt 12):3142-3148.

3. Holtmaat AJ, et al. (2005) Transient and persistent dendritic spines in the neocortex in vivo. Neuron45(2):279-291.

4. Hutsler JJ & Zhang H (2010) Increased dendritic spine densities on cortical projection neurons in autism spectrum disorders. Brain Res 1309:83-94.

5. Perez-Cruz C, et al. (2011) Reduced Spine Density in Specific Regions of CA1 Pyramidal Neurons in Two Transgenic Mouse Models of Alzheimer's Disease. Journal of Neuroscience 31(10):3926-3934.

6. Palombo M, et al. (2016) New paradigm to assess brain cell morphology by diffusion-weighted MR spectroscopy in vivo. Proc Natl Acad Sci U S A 113(24):6671-6676.

7. Palombo M, Ligneul C, & Valette J (2017) Modeling diffusion of intracellular metabolites in the mouse brain up to very high diffusion-weighting: Diffusion in long fibers (almost) accounts for non-monoexponential attenuation. Magnet Reson Med 77(1):343-350.

8. Vincent M, Palombo M, & Valette J (2019) Revisiting double diffusion encoding MRS in the mouse brain at 11.7 T: which microstructural features are we sensitive to? arXiv preprint.

9. Kroenke CD, Ackerman JJ, & Yablonskiy DA (2004) On the nature of the NAA diffusion attenuated MR signal in the central nervous system. Magn Reson Med 52(5):1052-1059.

10. Palombo M, Shemesh N, Ronen I, & Valette J (2017) Insights into brain microstructure from in vivo DW-MRS. Neuroimage.

11. Branzoli F, et al. (2016) Differentiating between axonal damage and demyelination in healthy aging by combining diffusion-tensor imaging and diffusion-weighted spectroscopy in the human corpus callosum at 7 T. Neurobiol Aging 47:210-217.

12. Ercan E, et al. (2016) Glial and axonal changes in systemic lupus erythematosus measured with diffusion of intracellular metabolites. Brain 139(Pt 5):1447-1457.

13. Lundell H, Ingo C, Dyrby TB, & Ronen I (2017) Accurate estimation of intra-axonal diffusivity and anisotropy of NAA in humans at 7T. Proc. Intl. Soc. Mag. Reson. Med. 25.

14. Najac C, Branzoli F, Ronen I, & Valette J (2016) Brain intracellular metabolites are freely diffusing along cell fibers in grey and white matter, as measured by diffusion-weighted MR spectroscopy in the human brain at 7 T. Brain Struct Funct 221(3):1245-1254.

15. Ronen I, Ercan E, & Webb A (2013) Axonal and glial microstructural information obtained with diffusion-weighted magnetic resonance spectroscopy at 7T. Front Integr Neurosci 7:13.

16. Ronen I, et al. (2014) Microstructural organization of axons in the human corpus callosum quantified by diffusion-weighted magnetic resonance spectroscopy of N-acetylaspartate and post-mortem histology. Brain Struct Funct 219(5):1773-1785.

17. Cao P & Wu EX (2017) In vivo diffusion MRS investigation of non-water molecules in biological tissues. Nmr Biomed 30(3).

18. Ronen I & Valette J (2015) Diffusion-weighted magnetic resonance spectroscopy. eMagRes 4:733–750.

19. Genovese G et al. (2018) Reproducibility and clinical feasibility of diffusion-weighted MRS using DW-sLASER and DW-STEAM in the human brain in vivo at 3T. Proceedings of the 26th Annual Meeting of ISMRM, 4447.

20. Provencher SW (1993) Estimation of metabolite concentrations from localized in vivo proton NMR spectra. Magn Reson Med 30(6):672-679.

21. Sukstanskii AL & Yablonskiy DA (2008) In vivo lung morphometry with hyperpolarized He-3 diffusion MRI: Theoretical background. J Magn Reson 190(2):200-210.

22. Yablonskiy DA & Sukstanskii AL (2010) Theoretical models of the diffusion weighted MR signal. Nmr Biomed 23(7):661-681.

23. Palombo M, Ligneul C, Hernandez-Garzon E, & Valette J (2017) Can we detect the effect of spines and leaflets on the diffusion of brain intracellular metabolites? Neuroimage.

24. Balinov B, Jonsson B, Linse P, & Söderman O (1993) The NMR Self-Diffusion Method Applied to Restricted Diffusion. Simulation of Echo Attenuation from Molecules in Spheres and between Planes J Magn Reson, Series A 104:17-25.

25. Palombo M, Alexander DC, & Zhang H (2019) A generative model of realistic brain cells with application to numerical simulation of the diffusion-weighted MR signal. Neuroimage 188:391-402.

26. Cook PA, et al. (2006) Camino: open-source diffusion-MRI reconstruction and processing. In 14th scientific meeting of the international society for magnetic resonance in medicine (Vol. 2759, p. 2759). Seattle WA, USA.

27. Sild M & Ruthazer ES (2011) Radial Glia: Progenitor, Pathway, and Partner. Neuroscientist 17(3):288-302.

28. Ingo C, Brink W, Ercan E, Webb AG, & Ronen I (2018) Studying neurons and glia non-invasively via anomalous subdiffusion of intracellular metabolites. Brain Structure & Function 223(8):3841-3854.

Figures

Fig.1 Location of the DW-MRS voxel in cerebellar (A) and cerebral posterior cingulate, PCC (B) cortex, together with estimated intra-voxel grey matter (GM) and white matter (WM) fractions from structural T1-weighted image. C) Schematic representation of the sequence used, with td/δ = 62.5/26.4 ms, inter-gradient separation 28.8 ms. D) Example of DW-MRS spectra at each b value for one subject, with tNAA, tCho and total creatine (tCr) peaks labeled, for cerebellar (left) and cerebral (right) cortex.

Fig.2 DW-MRS signals as a function of b for tCho and tNAA from VOI in the cerebellar and cerebral cortex. Error bars are standard error of the mean. Straight lines are the result of best non-linear fitting Eq.[1] to experimental data by using Matlab (The Mathworks) lsqcurvefit function with trust-reflective method. Gray stars indicate DW-MRS signal intensities statistically different.

Fig.3 Estimated model parameters D₀, d and β for data in Fig.2. 2000 different realizations of signal decay were drawn by adding Gaussian noise to experimental data in Fig.2 with standard deviation equal to the residuals of best fit, then fitted using Eq.[1]. The mean and standard deviation of the 2000 estimated values for D₀, d and β were computed and here shown as colored bars, and error bar respectively. Gray stars indicate statistically significant differences.

Fig.4 A) Examples of complex three-dimensional computational models of cell morphologies at different combinations of spine density ρ_spine and soma radius (R_soma) used in Monte-Carlo simulation of DW-MRS signal. Cell fibre's diameter d=1 μm and soma volume fraction fixed to 0.20. B) Estimated D₀ and β from fitting Eq.[1] to the simulated signal for each (R_soma, ρ_spine) combination.

Proc. Intl. Soc. Mag. Reson. Med. 28 (2020)

0846