Introduction

Diffusion MRI (dMRI) inside axons of brain white matter (WM) is non-Gaussian, as manifested by diffusivity time-dependence and a non-trivial kurtosis either transverse to or along axons, and indicates its sensitivity to axonal shape variation. Here, for the first time we perform Monte Carlo (MC) simulations within intra-axonal space (IAS) segmented from human brain subcortical WM. We validate analytical models of time-dependent diffusion, and compare results with those from mouse brain corpus callosum (CC)^[1,2].

Methods

$$$\textit{Electron microscopy of human brain}$$$

Human brain sample was obtained from the posterior left middle temporal gyrus of a 47-year-old female during surgical operation for the removal of an epileptogenic focus in the left hippocampus. The tissue sample is fixed with glutaraldehyde/paraformaldehyde, stained with osmium tetroxide and embedded in Epon resin^[3]. The sample containing cerebral cortex and subcortical WM was trimmed to 2mm$$$\times$$$3mm$$$\times$$$200$$$\mu$$$m and scanned with serial-section scanning EM (Sigma, Carl Zeiss)^[4]. The 8$$$\times$$$8$$$\times$$$39$$$\mu$$$m$$$^3$$$ subset of subcortical WM was segmented using 2$$$d$$$/3$$$d$$$ U-Net^[5], which was initially trained on the mouse EM data in CC with ground truth segmentation of myelin and IAS^[1]. Voxel size was downsampled to 32$$$\times$$$32$$$\times$$$30nm$$$^3$$$.

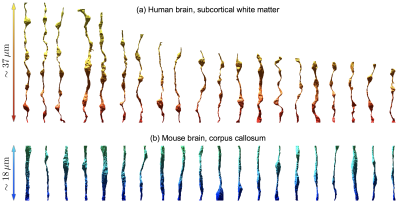
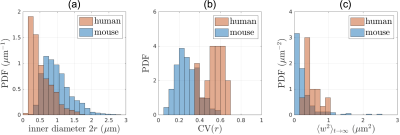
Segmented IASs of myelinated axons longer than 20$$$\mu$$$m were aligned along the z-axis and truncated at both ends, resulting in 20 axons 18-37$$$\mu$$$m long (Fig.1a). Further, we compare IASs from human brain WM with those from mouse brain CC^[1] (Fig.1b), in terms of inner diameter $$$2r$$$, caliber variation (i.e. coefficient of variation of radius, CV($$$r$$$)), and undulation variance $$$\langle{}w^2\rangle_{t\to\infty}$$$ (variance of the deviation from the axonal skeleton perpendicular to the main axis), Eq.(1b) below.

$$$\textit{Monte Carlo simulations}$$$

MC simulations were implemented in CUDA C++^[2,6] for diffusion in the 3$$$d$$$ micro-geometry consisting of IAS from all 20 axons. 1$$$\times$$$10$$$^7$$$ random walkers/fiber were employed in 20 segmented IASs, diffusing 5$$$\times$$$10$$$^5$$$ steps with a duration $$$\delta{}t$$$=8$$$\times$$$10$$$^{-5}$$$ms and a length $$$\sqrt{6D_0\delta{}t}$$$=31nm for each step. The intrinsic diffusivity is set to $$$D_0$$$=2$$$\mu$$$m$$$^2$$$/ms. Maximal diffusion time was $$$t$$$=400ms. Calculations took 6 hours on 20 NVIDIA GPU cores.

Axial/radial diffusivity (AD, RD) and kurtosis (AK, RK) were computed based on the cumulants of diffusion displacements.

$$$\textit{Theory}$$$

For diffusion transverse to axons, considering the coherent averaging within a coarse-graining window along the axon, the diffusion-diffraction long-time limit of the propagator yields the RD^[7]:
$$D_\perp(t)\simeq\frac{r_{\rm{}eff}^2}{4t}\,,\quad\quad(1a)$$
$$r_{\rm{}eff}^2\simeq\langle{}r^2\rangle_v+\langle w^2\rangle_{t\to\infty}\,,\quad\quad(1b)$$
where $$$r_{\rm{}eff}$$$ is the dMRI-relevant effective axon radius, $$$\langle{}r^2\rangle_v\equiv\langle{}r^4\rangle/\langle{}r^2\rangle$$$ is the volume-weighted radius estimation from histology, and $$$\langle{}w^2\rangle$$$ is the undulation variance^[8,9,10].
Similarly, the RK in $$$t\to\infty$$$ limit is given by^[10]
$$K^\perp_\infty\simeq\frac{\langle{}r^6\rangle\langle{}r^2\rangle}{\langle{}r^4\rangle^2}-\frac{3}{2}\,,\quad\quad(2)$$
whose minimal value $$$-1/2$$$ is reached for a perfectly straight cylinder^[7].

For diffusion along axons, randomly positioned restrictions (e.g., beads) along axon lead to following AD time-dependence^[11,12]:
$$D_\parallel(t)\simeq{}D^\parallel_\infty+c\cdot{}t^{-\vartheta}\,,\quad\vartheta=\frac{1}{2}\,,\quad\quad(3)$$
where the dynamical exponent $$$\vartheta=1/2$$$ is hallmark for short-range disorder in 1$$$d$$$. It was shown previously that stronger caliber variations (e.g., higher bead density/amplitude) lead to lower $$$D^\parallel_\infty$$$^[13], manifested by^[2]
$$\left(\frac{D_0}{D^\parallel_\infty}-1\right)\propto{\rm{}CV}^2(r)\,.\quad\quad(4)$$

Results

Structure: In human brain subcortical WM (Fig.2), we find mean inner diameter $$$2\langle{}r\rangle$$$=0.53$$$\pm$$$0.31$$$\mu$$$m, CV($$$r$$$)=0.53$$$\pm$$$0.10, and $$$\langle{}w^2\rangle_{t\to\infty}$$$=0.52$$$\pm$$$0.22$$$\mu$$$m$$$^2$$$.
For comparison, in mouse brain CC, mean inner diameter $$$2\langle{}r\rangle$$$=0.99$$$\pm$$$0.40$$$\mu$$$m, CV($$$r$$$)=0.28$$$\pm$$$0.11, and $$$\langle{}w^2\rangle_{t\to\infty}$$$=0.28$$$\pm$$$0.38$$$\mu$$$m$$$^2$$$.

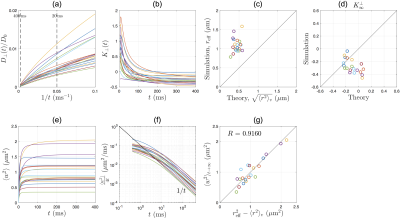
Radial diffusion: Simulations in human IAS show that RD scales as $$$1/t$$$ at long time (Fig.3a), and RK approaches a negative constant at long time (Fig.3b). The dMRI-measured effective radius $$$r_{\rm{}eff}$$$ in Eq.(1a) is larger than histology-based estimation $$$\langle{}r^2\rangle_v$$$ in Eq.(1b) by a factor of 2.5 (Fig.3c).
The RK in $$$t\to\infty$$$ limit is $$$\sim-0.2$$$ (Fig.3d), very different from that in a perfect cylinder. Furthermore, we demonstrate the effect of axonal undulations on the diffusion metrics: The undulation variance $$$\langle{}w^2\rangle$$$ due to the diffusion along axonal skeleton grows with time and approaches a constant at long time, leading to a diffusivity contribution transverse to the axon $$$\simeq\langle{}w^2\rangle/(4t)\propto{}1/t$$$ (Fig.3f). Remarkably, the discrepancy in dMRI-measured effective radius $$$r_{\rm{}eff}^2$$$ and histology-based estimation $$$\langle{}r^2\rangle_v$$$ (Fig.3c) can be solely explained by the axonal undulation contribution $$$\langle{}w^2\rangle_{t\to\infty}$$$ (Fig.3g).


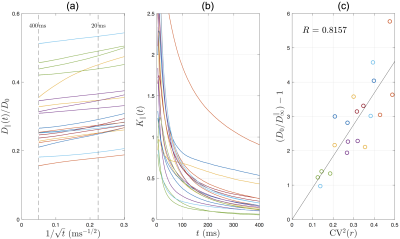
Axial diffusion: The simulated AD in human IAS scales as $$$1/\sqrt{t}$$$ in most of the axons (Fig.4a), with a time-dependence amplitude $$$c\approx$$$0.1-0.5$$$\mu$$$m$$$^2$$$/ms$$$^{1/2}$$$, consistent with previous in vivo observations^[2]. The simulated AK decreases with time and approaches to a positive constant (Fig.4b). The relationship between long-time AD and caliber variation in Eq.(4) is tested in Fig.4c, where the high correlation indicates that long-time AD decreases due to increasing caliber variation (or increasing beading).

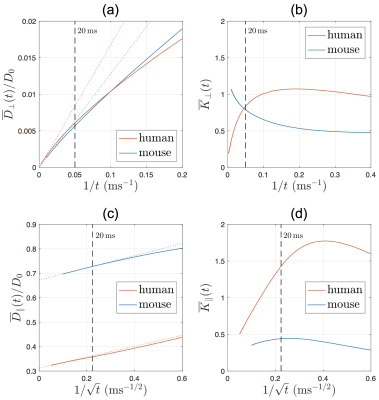
Comparison between human and mouse for simulated intra-axonal AD/AK/RD/RK is shown in Fig.5.

Discussion and Conclusions

Our overarching result is that the first-ever MC simulations of diffusion inside EM-segmented human axons confirm non-Gaussian time-dependent intra-axonal diffusion, and validate the proposed diffusion models in both radial and axial directions.

Comparing human and mouse, our MC results (Fig.5) exhibit similar functional forms of time-dependence both transverse and along axons. The RD time-dependence is stronger in human (Fig.5a) due to corresponding larger undulation $$$\langle{}w^2\rangle_{t\to\infty}$$$ (Fig.2c). In addition, the long-time AD is lower in human due to corresponding larger caliber variation CV($$$r$$$) (Fig.2b, Eq.(4)). The amplitude of AD time-dependence is similar between mouse and human data (Fig.5c).

Numerical simulations in 3$$$d$$$ EM-segmented micro-geometry serve as a critical validation step for biophysical model, in order to obtain quantitative biomarkers (e.g., axonal diameter, caliber variation, undulation) for potential clinical applications.

Acknowledgements

We would like to thank NYULH Bigpurple for the high-performance-computing. Research was supported by the National Institute of Neurological Disorders and Stroke of the NIH under award number R01 NS088040 and R21 NS081230, and NIH U01EB026996, and was performed at the Center of Advanced Imaging Innovation and Research (CAI2R, www.cai2r.net), an NIBIB Biomedical Technology Resource Center (NIH P41 EB017183).