0791

Quantifying the underestimation of myocardial extra cellular volume fraction measurements due to transcytolemmal water exchange

Andrew D Scott^1,2, Peter D Gatehouse^1,2, and David N Firmin^1,2
¹CMR Unit, The Royal Brompton Hospital, London, United Kingdom, ²National Heart and Lung Institute, Imperial College London, London, United Kingdom

Synopsis

MR based measures of myocardial extra cellular volume fraction (ECV) obtained from pre and post-contrast T1 mapping are frequently used in research studies. However, typically ECV calculations rely on rapid exchange of water molecules between the intra and extracellular space. We assess the validity of the shutter speed approximation of the full two-compartment model and use this model to assess the effect of limited water exchange rate between the cardiomyocytes and interstitial fluid. For typical conditions used in measuring ECV, we demonstrate an underestimation of ECV on a similar magnitude to the changes attributed to disease in some studies.

Introduction

Myocardial extracellular volume fraction (ECV) measurement based on T1 mapping pre and post-administration of extracellular gadolinium-based contrast agent (GBCA) is a well-established method¹. Such methods use the change in blood and myocardial T1, with blood cellular volume fraction (haematocrit, Hct) and the assumption of equilibration of myocardial interstitial fluid (MIF) and blood plasma GBCA concentration². However, one frequently acknowledged, but rarely studied limitation is the finite lifetime of water molecules in the intracellular space (τ_i) due to cardiomyocyte volume and the finite membrane permeability – surface area product³. Here we estimate errors in ECV measures due to finite τ_i using the shutter-speed approximation of the two-compartment model⁴.

Methods

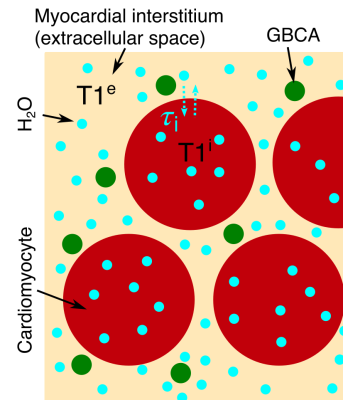
We initially determine the validity of the shutter-speed model in myocardium.

A tissue containing two exchanging compartments (figure 1) with T1s (in the absence of exchange) T1^e and T1ⁱ, demonstrates bi-exponential recovery of image intensity, S, according to:
$$S=S_0∙[a⋅f(t,T1^a )+b⋅f(t,T1^b )] (1)$$
where S₀ is the initial signal intensity and:
$$f(t,T1^{a/b} )=1-2∙e^{\frac{-t}{T1^{a/b}}} (2)$$
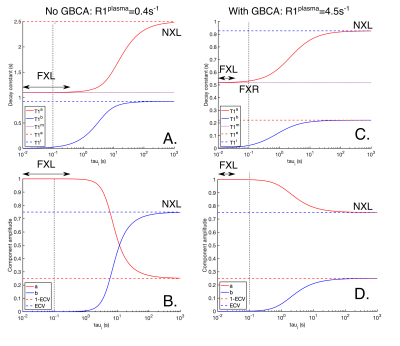
for an inversion recovery sequence, where t is the inversion time. T1^a and T1^b are the measurable T1s. For very fast exchange between the compartments (small cells, high membrane permeability/surface area, short τ_i, known as the fast exchange limit (FXL)), one of a and b is negligible and the apparent relaxation time (T1^m) is the population weighted average of T1ⁱ and T1^e:
$$\frac{1}{T1^m} =\frac{ECV}{T1^e} +\frac{1-ECV}{T1^i} (3)$$
When there is no exchange (the no exchange limit, NXL, long τ_i), a and b are the relative intra and extracellular populations (a+b=1) and T1^a and T1^b are equal to T1^e and T1ⁱ. In the intermediate regime, a, b, T1^a and T1^b depend on τ_i via the more complex two-compartment exchange model⁵. However, in the fast exchange regime (FXR, τ_i(FXR) > τ_i(FXL)) or shutter-speed model, the smaller component of a or b is negligible, but there is a measurable change in the apparent T1.

We assume FXL in blood (erythrocytes high surface area to volume ratio, therefore short τ_i). Pintaske et al.⁶ measured native plasma R1 (1/T1) R1^{plasma pre}=0.4±0.1s^-1 at 3T. As blood plasma and MIF are both extracellular fluids, we assume R1^{plasma pre}=R1^{MIF pre}. Using a pre-contrast, whole myocardium R1^myo
pre=0.91s^-1 ⁷, myocardial ECV=25% and equation 1 (i.e. FXL without GBCA), gives R1ⁱ (=1/T1ⁱ)=1.08s^-1 in cardiomyocytes.

Based on R1^{plasma pre}=0.4s^-1, Hct=0.4 and pre-contrast blood R1^{blood pre}=0.625s^-1 ⁸, gives erythrocytes R1^RBC=0.96s^-1. A GBCA dose of 0.2mmol kg^-1 with a relaxivity of 4.5 Lmmol^-1s^-1 ⁶ distributed throughout a 70kg man (plasma volume 3L⁹ and total interstitial volume 5x plasma¹⁰) gives R1^{blood post}=3.1s^-1 and R1^{plasma post}=4.5s^-1.

Using these values we simulated the two-compartment exchange model to test the validity of the shutter-speed model. We therefore used the shutter-speed model (FXR) to estimate the error in ECV (calculated assuming FXL between cardiomyocytes and MIF) due to transcytolemmal water exchange. Using the FXL approximation and assuming equal plasma and MIF GBCA concentration, ECV is:
$$\frac{ECV}{1-Hct}=\frac{R1^{myo post}-R1^{myo pre}}{R1^{blood post}-R1^{blood pre}} (4)$$
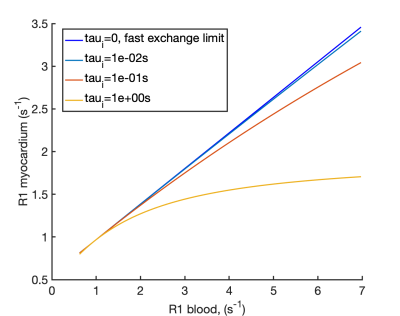
The myocardial R1^{myo post} is therefore linearly related to the blood R1^{blood post} in FXL. We simulated R1^{myo post} for variable GBCA concentrations (R1^blood
post) using the shutter-speed model to investigate the deviation of R1^myo
post from the FXL. Using the simulated exchange modified R1^{myo post} and R1^{blood post} we calculated the ECV that would be obtained using equation 4, as typically employed in ECV studies.

Results

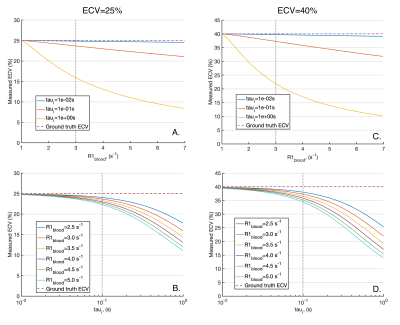
Figure 2 plots the apparent R1s and their amplitudes for varying τ_i pre-contrast (A and B) and post-contrast (C and D). Pre-contrast, at myocardial τ_i=100ms^3,11, the smaller component of the biexponential (b) has amplitude b=5x10^-5 and T1^a is equal to the population weighted average (T1^m), suggesting the FXL. Post contrast, at τ_i=100ms^3,11, b=1.3x10^-3, but T1^a is increased by 14ms over T1^m due to the effects of exchange, suggesting that the shutter-speed approximation or FXR¹² is applicable.

Based on the FXR/shutter-speed approximation, figure 3 shows the non-linearity of R1^{myo post} with R1^{blood post} at high GBCA as a consequence of finite τ_i. Figure 4 shows measured ECV if the exchange modified R1^{myo post} is used in equation 4. At ground truth ECV=25%, τ_i=100ms and R1^{blood post}=3s^-1, the measured ECV=23.6% and at ground truth ECV=40%, measured ECV=37.2%. Figure 5 shows the error in ECV as a function of ECV.

Discussion

Based on a two-compartment model of T1, the myocardium is in the FXL pre-contrast and FXR with typical GBCA doses. In FXR the shutter-speed model applies and we estimated the error in measured ECV due to limited water exchange between the intracellular space and MIF. The typical underestimation in ECV is 1.5-3% for ground truth ECV=25-40%. However, these errors increase with R1^blood and intracellular water lifetime (τ_i). While R1^blood can be reported to help identify potential exchange related changes, τ_i is more challenging to measure.

Coelho-Filho et al.¹¹ compared the FXL based ECV with a shutter-speed model estimate of ECV and demonstrate larger changes in-vivo than our 1.5-3%, although their peak R1^blood was higher.

Conclusion

Measured differences in ECV on the scale of the underestimations demonstrated here (e.g. ^13,14) should be interpreted with caution as they could be a consequence of τ_i variation due to changes in cell volume, surface area or permeability rather than in ECV.

Acknowledgements

This work was partly funded by the British Heart Foundation (RG/19/1/34160).

References

1. Haaf, P. et al. Cardiac T1 Mapping and Extracellular Volume (ECV) in clinical practice: A comprehensive review. Journal of Cardiovascular Magnetic Resonance 18, (2016).

2. Arheden, H. et al. Reperfused rat myocardium subjected to various durations of ischemia: Estimation of the distribution volume of contrast material with echo-planar MR imaging. Radiology 215, 520–528 (2000).

3. Donahue, K. M., Burstein, D., Manning, W. J. & Gray, M. L. Studies of Gd‐DTPA relaxivity and proton exchange rates in tissue. Magn. Reson. Med. 32, 66–76 (1994).

4. Yankeelov, T. E., Rooney, W. D., Li, X. & Springer, C. S. Variation of the Relaxographic ‘Shutter-Speed’ for Transcytolemmal Water Exchange Affects the CR Bolus-Tracking Curve Shape. Magn. Reson. Med. (2003). doi:10.1002/mrm.10624

5. Callaghan, P. T. Spin relaxation in microscopically inhomogeneous media. in Translational Dynamics and Magnetic Resonance 261–269 (Oxford University Press, 2011).

6. Pintaske, J. et al. Erratum: Relaxivity of gadopentetate dimeglumine (Magnevist), gadobutrol (Gadovist), and gadobenate dimeglumine (MultiHance) in human blood plasma at 0.2, 1.5, and 3 Tesla (Investigative Radiology (2006) 41,3, (213-221)). Investigative Radiology (2006). doi:10.1097/00004424-200612000-00003

7. Roy, C. et al. Age and sex corrected normal reference values of T1, T2 T2∗and ECV in healthy subjects at 3T CMR. J. Cardiovasc. Magn. Reson. (2017). doi:10.1186/s12968-017-0371-5

8. Lu, H., Clingman, C., Golay, X. & Van Zijl, P. C. M. Determining the longitudinal relaxation time (T1) of blood at 3.0 tesla. Magn. Reson. Med. 52, 679–682 (2004).

9. Feldschuh, J. & Enson, Y. Prediction of the normal blood volume. Relation of blood volume to body habitus. Circulation (1977). doi:10.1161/01.CIR.56.4.605

10. Tortora, G. J. & Derrickson, B. Principles of Anatomy & Physiology. (Wiley, 2014).

11. Coelho-Filho, O. R. et al. Role of transcytolemmal water-exchange in magnetic resonance measurements of diffuse myocardial fibrosis in hypertensive heart disease. Circ. Cardiovasc. Imaging (2013). doi:10.1161/CIRCIMAGING.112.979815

12. Buckley, D. L. Shutter-speed dynamic contrast-enhanced MRI: Is it fit for purpose? Magn. Reson. Med. 81, 976–988 (2019).

13. Ntusi, N. A. B. et al. Diffuse myocardial fibrosis and inflammation in rheumatoid arthritis: Insights from CMR T1 Mapping. JACC Cardiovasc. Imaging (2015). doi:10.1016/j.jcmg.2014.12.025

14. Su, M. Y. M. et al. CMR-verified diffuse myocardial fibrosis is associated with diastolic dysfunction in HFpEF. JACC Cardiovasc. Imaging (2014). doi:10.1016/j.jcmg.2014.04.022

Figures

Figure 1: Schematic of the myocardial model used. The intra and extracellular spaces have exchange free T1 values of T1ⁱ and T1^e respectively and the mean intracellular residence time for a water molecule is τ_i. GBCA remains in the extracellular space, but water molecules can transit across the cell membrane. ECV is the volume of extra cellular space as a proportion of the total.

Figure 2: Apparent T1 (T1^a and T1^b) (A and C) and the relative amplitudes (a and b) of the two exponential components (B and D) as ti is increased, without GBCA (R1^plasma=0.4s^-1, A and B) and with GBCA (R1^plasma=4.5s^-1). At expected myocardial τ_i (100ms, dotted grey line) without GBCA, the myocardium is in the fast exchange limit (FXL) as b~0 and T1^a=T1^m. With GBCA (τ_i=100ms), again b~0 (D), but there is a measurable change in T1^a (C). This regime is known as the fast exchange regime (FXR). Note that GBCA causes T1^e to increase from T1^e>T1ⁱ (A) to T1^e<T1ⁱ(B).

Figure 3: As the rate of exchange between intra and extracellular space reduces (increasing τ_i), the myocardial R1 is reduced from the FXL linear relationship (τ_i=0). ECV=25% in this simulation. In-vivo measurements of blood and myocardial R1 with varying GBCA concentration have shown similar plots¹¹.

Figure 4: The change in measured ECV as a result of non-zero τ_i at ground truth ECV=25% (A and B, approximate healthy value) and at a pathologically high ECV=40% (C and D). More underestimation of ECV occurs, either as R1^blood increases with increasing GBCA concentration (A and C) or as a result of slower exchange (longer τ_i) between intra and extracellular space (B and D), the error in measured ECV increases. Dotted vertical grey lines show typical R1^blood (for approximately 15mins post 0.2mmol kg^-1 GBCA dose, A and C) and expected τ_i (100ms, B and D).

Figure 5: The error in ECV as a function of ECV for a range of τ_i (A) and R1^blood (B). R1^blood is 3s^-1 in A and τ_i=100ms in B.

Proc. Intl. Soc. Mag. Reson. Med. 28 (2020)

0791