0775

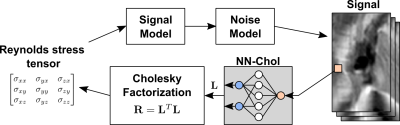
Improved In Vivo Estimation of the Reynolds Stress Tensor from 4D und 5D Flow MRI Using Cholesky Decomposition-Based Neural Networks
Valery Vishnevskiy1,2, Hannes Dillinger1,2, Jonas Walheim1,2, Lin Zhang1, and Sebastian Kozerke1,2
1ETH Zurich, Zurich, Switzerland, 2University of Zurich, Zurich, Switzerland

Synopsis

A novel approach using Cholesky decomposition-based neural networks for the estimation of Reynolds stress tensors in 4D Flow MRI is presented. Evaluation is carried out for simulated MRI signals using particle tracking velocimetry data and tested on in-vivo data obtained in a healthy volunteer and a patient with bioprosthetic aortic valve. The proposed method allows to account for non-Gaussian acquisition noise and guarantees positive-definiteness of the estimated tensors, which yields 68% improvement in turbulent shear stress estimation compared to standard least squares estimation.

Introduction

The derivation of mean and turbulent flow components from 4D Flow MRI data promises detection of elevated shear stresses [5,6] in valve stenoses [1,2,3,4]. However, the comprehensive assessment of turbulent flow requires derivation of the entire Reynolds stress tensor (RST) which can be determined by encoding velocities along at least 6 non-collinear directions and subsequent solving a system of linear equations [8,15], typically using the least-squares fit solution (LSQ). LSQ, however, imposes Gaussian assumptions on the acquisition noise model which may not be fulfilled in low SNR scenarios and in the presence of partial voluming given limited spatial resolution in 4D Flow MRI. In this work, a Cholesky-based neural network (NN) approach is developed and applied for estimating the RST. The proposed method is tested against LSQ for a multipoint Flow MRI encoding strategy [5,16]. Results demonstrate that the proposed approach outperforms LSQ for a wide range of SNR values and for different error metrics.

Methods

The magnitude of the measured signal in 4D Flow MRI can be written as [5]:
$$$|S_{\mathbf{k}_{vi}}|=|S_0|\exp{\left(−\frac{1}{2\rho}\mathbf{k}_{vi}^T\,\mathbf{R}\,\mathbf{k}_{vi} \right)},\quad\quad(*)$$$
where $$$S_{0}$$$ denotes the signal obtained without velocity encoding, $$$\rho$$$ the fluid density and $$$\mathbf{k}_{vi}=[{k}_{v_xi}, {k}_{v_yi}, {k}_{v_zi}]$$$ defines velocity encoding directions and strengths. After log-transform of the normalized signal values for a given set of , a system of linear equations can be solved in the least squares sense to estimate values of at each voxel. In regions of high signal attenuation (e.g. the border of a stenotic jet) and low SNR, the problem can get ill-conditioned yielding RST underestimation due to non-Gaussian acquisition noise [11]. Thresholding based on noise levels in the data has been proposed [12]. In contrast, our approach leverages information of all velocity encodings to reconstruct the RST from noisy data.
The idea of learning an estimation function in the form of a neural network from synthetic simulations has great potential for isotropic models [10, 17]. However, direct optimization of predicted tensor values (referenced as NN) does not guarantee a symmetric positive-definite (SPD) estimate and can result in tensor “swelling” [18]. Therefore we employ the fact that any SPD matrix allows Cholesky decomposition: $$$\mathbf{R}=\mathbf{L}^T\mathbf{L},$$$where is $$$\mathbf{L}$$$ a triangular matrix with a positive diagonal. The inference neural network (NN-Chol in Figure 1) consists of 5 hidden fully connected layers with hyperbolic tangent activation functions and maps the input signal into the Cholesky factor $$$\mathbf{L}$$$ of the tensor. The diagonal of the output is guaranteed to be positive via exponentiation.The network was trained to minimize the L1 error of Cholesky factor prediction using the Adam algorithm [19] for $$$5\cdot10^4$$$ iterations with batch size 5000 for tensors with random orientations and anisotropicity, while its trace was uniformly distributed on a [0, 1500] J/m3 interval and the acquisition SNR>10.
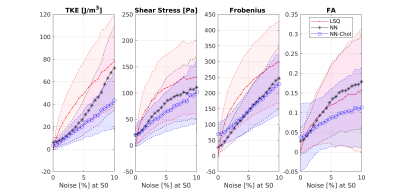
Tensor estimates were evaluated using the sum of absolute errors for turbulent kinetic energy ($$$\text{TKE}(\mathbf{R})= \sum_i\lambda_i(\mathbf{R})$$$), turbulent shear stress ($$$\text{TSS}(\mathbf{R})=(\lambda_1(\mathbf{R})−\lambda_3(\mathbf{R}))/2$$$), Frobenius norm and fractional anisotropy (FA) calculated for each voxel separately, where $$$\lambda_i(\mathbf{R})$$$ are eigenvalues of $$$\mathbf{R}$$$ in descending order.

Results

In-vitro data
Synthetic MR signal was simulated using tensor data from particle tracking velocimetry (PTV) [13], assuming encoding strengths $$$v_\text{enc}$$$ of 50, 150, 450 cm/s and a normal+bisecting encoding scheme [9] according to Equation (*), assuming $$$\rho=1060 \mathrm{kg/m}^3$$$. Regions of interest [13] are shown in Figure 2. Rician noise according to SNR levels from infinite to 10 was added to the data and used for evaluation.
Spatial TKE and TSS maps in Figure 2 indicate that LSQ fitting requires high SNR to accurately estimate the Reynolds stress tensor for high TKE values, while the proposed NN-Chol approach does not show any significant bias in TKE and TSS values for SNR of 20. Tensor estimation metrics evaluated inside the jet core with various SNR levels are reported in Figure 3 and show that NN-Chol outperforms LSQ for all realistic acquisition scenarios (SNR < 100), and supports the claim that training for direct prediction of tensor values (cf. NN) increases the error of FA and TSS estimation.

In-vivo data
4D Flow MRI data of a healthy volunteer and a patient with a bioprosthetic valve (SJM Trifecta Aortic Valve, Model TFGT-21A, diameter 21 mm) were acquired using the 5D Flow Tensor MRI approach [14] on a clinical 3T MRI system (Philips Healthcare, Best, The Netherlands) upon written informed consent of the subjects and according to local ethics regulations.
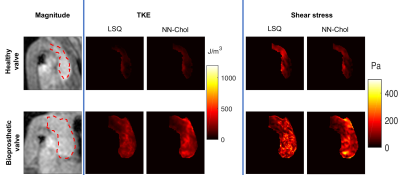
Exemplary slices shown in Figure 4 with TKE and TSS maps inside a manually segmented region of interest of aorta show that NN-Chol provides smoother estimates compared to LSQ. The distribution of TKE and TSS values in healthy and bioprosthetic subjects are shown in Figure 5. The NN-Chol estimation allows for an improved differentiation between patient and control (53±28 J/m3 vs 177±85J/m3 (TKE) and 40±23 Pa vs 121±74 Pa (TSS)) compared to LSQ fitting (37±29 J/m3 vs 133±52 J/m3 (TKE) and 62±41 Pa vs 116±60 PA (TSS)).

Conclusion

In this work we have developed an efficient neural architecture for Reynolds stress tensor estimation from 4D and 5D Flow MRI. Compared to LSQ fitting the proposed NN-Chol improves TKE and TSS estimation accuracy inside the jet core by 53% and 68% respectively for acquisition SNR of 20.

Acknowledgements

The authors acknowledge funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No 668039.

References

1. Binter C, Gotschy A, Sündermann SH, Frank M, Tanner FC, Lüscher TF, Manka R, Kozerke S. Turbulent Kinetic Energy Assessed by Multipoint 4-Dimensional Flow Magnetic Resonance Imaging Provides Additional Information Relative to Echocardiography for the Determination of Aortic Stenosis Severity. Circulation: Cardiovascular Imaging. 2017;10(6):1–8.

2. Haraldsson H, Kefayati S, Ahn S, Dyverfeldt P, Lantz J, Karlsson M, Laub G, Ebbers T, Saloner D. Assessment of Reynolds stress components and turbulent pressure loss using 4D flow MRI with extended motion encoding. Magnetic Resonance in Medicine. 2018;79(4):1962–1971.

3. Casas B, Lantz J, DyverfeldT P, Ebbers T. 4D Flow MRI-based pressure loss estimation in stenotic flows: Evaluation using numerical simulations. Magn. Reson. Med. 2016;75:1808–1821.

4. Ha H, Kvitting J-PE, Dyverfeldt P, Ebbers T. Validation of pressure drop assessment using 4D flow MRI-based turbulence production in various shapes of aortic stenoses. Magn. Reson. Med. 2018:1–14.

5. Binter C, Knobloch V, Sigfridsson A, Kozerke S. Direct quantification of turbulent shear stresses by multi-point phase-contrast MRI. In: Proceedings of the International Society for Magnetic Resonance in Medicine. ; 2012. p. 20.

6. Ha H, Kvitting J-PE, Dyverfeldt P, Ebbers T. 4D Flow MRI quantification of blood flow patterns, turbulence and pressure drop in normal and stenotic prosthetic heart valves. Magn. Reson. Imaging 2019;55:118–127.

7. Walheim J, Dillinger H, Kozerke S. Multipoint 5D Flow cardiovascular magnetic resonance -accelerated cardiac- and respiratory-motion resolved mapping of mean and turbulent velocities. J. Cardiovasc. Magn. Reson. 2019 doi: 10.1186/s12968-019-0549-0.

8. Ha H, Lantz J, Haraldsson H, et al. Assessment of turbulent viscous stress using ICOSA 4D Flow MRI for prediction of hemodynamic blood damage. Sci. Rep. 2016;6:1–14 doi: 10.1038/srep39773.

9. Elkins CJ, Alley MT, Saetran L, Eaton JK. Three-dimensional magnetic resonance velocimetry measurements of turbulence quantities in complex flow. Exp. Fluids 2009;46:285–296 doi: 10.1007/s00348-008-0559-4.

10. Zhang L, Vishnevskiy V, Jakab A, Goksel O. Implicit Modeling With Uncertainty Estimation For Intravoxel Incoherent Motion Imaging. 2019:1003–1007 doi: 10.1109/isbi.2019.8759391.

11. Ha H, Kim GB, Kweon J, et al. Turbulent kinetic energy measurement using phase contrast MRI for estimating the PostStenotic pressure drop: In vitro validation and clinical application. PLoS One 2016;11:1–14 doi: 10.1371/journal.pone.0151540.

12. Ha H, Kvitting JPE, Dyverfeldt P, Ebbers T. Validation of pressure drop assessment using 4D flow MRI-based turbulence production in various shapes of aortic stenoses. Magn. Reson. Med. 2019;81:893–906 doi: 10.1002/mrm.27437.

13. Binter C, Gülan U, Holzner M, Kozerke S. On the accuracy of viscous and turbulent loss quantification in stenotic aortic flow using phase-contrast MRI. Magn. Reson. Med. 2016;76:191–196 doi: 10.1002/mrm.25862.

14. Walheim J, Dillinger H, Kozerke S. 5D Flow tensor MRI for mapping Reynolds stresses in the aorta. ISMRM 2019.

15. Hasan KM, Parker DL, Alexander AL. Comparison of gradient encoding schemes for diffusion-tensor MRI. Journal of Magnetic Resonance Imaging. 2001;13(5):769–780.

16. Binter C, Knobloch V, Manka R, Sigfridsson A, Kozerke S. Bayesian multipoint velocity encoding for concurrent flow and turbulence mapping. Magnetic Resonance in Medicine. 2013;69(5):1337–1345.

17. Bertleff M, Domsch S, Weingärtner S, Zapp J, O'Brien K, Barth M, Schad LR. Diffusion parameter mapping with the combined intravoxel incoherent motion and kurtosis model using artificial neural networks at 3 T. NMR in Biomedicine. 2017 Dec;30(12).

18. Arsigny V, Fillard P, Pennec X, Ayache N. Log‐Euclidean metrics for fast and simple calculus on diffusion tensors. Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine. 2006 Aug;56(2):411-21.

19. Kingma DP, Ba J. Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980. 2014 Dec.

Figures

Figure 1: Cholesky neural network architecture for Reynolds stress tensor estimation. The network outputs 6 values that form the triangular matrix L. Training is performed using synthetic MRI signals and noise models.

Figure 2: Turbulent kinetic energy (TKE) and turbulent shear stress (TSS) maps estimated using LSQ and the proposed NN-Chol approach. The MRI signal was simulated from PTV data and noise added. The noisy signal was used as input for the prediction.

Figure 3: Mean +/- standard deviation (solid / dashed lines) of absolute tensor estimation error metrics for different noise levels (x-axis) evaluated on the synthetic model inside the jet core. The NN and NN-Chol outperform LSQ for noise levels above 1%.

Figure 4: In vivo evaluation of flow through healthy and bioprosthetic heart valves. TKE and turbulent shear stresses are shown for the ROI depicted on the left.

Figure 5: In vivo evaluation of turbulent kinetic energy and turbulent shear stress estimates averaged over manually segmented flow jet masks for healthy and bioprosthetic valves.

Proc. Intl. Soc. Mag. Reson. Med. 28 (2020)
0775