0773
Leveraging Anatomical Similarity for Unsupervised Model Learning and Synthetic MR Data Generation
Thomas Joyce1 and Sebastian Kozerke1
1Institute for Biomedical Engineering, University and ETH Zurich, Zurich, Switzerland
1Institute for Biomedical Engineering, University and ETH Zurich, Zurich, Switzerland
Synopsis
We present a method for the controllable synthesis of 3D (volumetric) MRI data. The model is comprised of three components which are learnt simultaneously from unlabelled data through self-supervision: i) a multi-tissue anatomical model, ii) a probability distribution over deformations of this anatomical model, and, iii) a probability distribution over ‘renderings’ of the anatomical model (where a rendering defines the relationship between anatomy and resulting pixel intensities). After training, synthetic data can be generated by sampling the deformation and rendering distributions.
Introduction
Image synthesis techniques have recently improved significantly, and synthetic data has been effectively leveraged in a broad range of medical imaging tasks1-4. However, current medical image synthesis approaches have a number of limitations. Firstly, there is limited progress on generation of 3D (volumetric) images. Secondly, controllable image synthesis, in which image generation can be meaningfully conditioned on some input (such as a dense semantic mask) is under explored in the medical setting. Lastly, synthesis of labelled data (e.g. data with multi-class segmentation masks) is strictly more useful than unlabelled image synthesis, but many papers focus on unlabelled image synthesis, or synthesis restricted to binary classes1,3 In this abstract we demonstrate an approach to address these problems. The proposed model learns a factored representation of 3D cardiac MRI data which it then leverages to generate diverse and realistic synthetic images with corresponding dense labels (Fig.1). As a second step we demonstrate that the resulting dense segmentation masks can be used with state-of-the-art conditional image synthesis models5 to generate sharp, high resolution synthetic image data, and that moreover, this synthesis is controllable by varying the anatomical segmentation mask.Methods
The proposed approach consist of an anatomical model, variational encoder-decoder networks, a transformer network and a rendering network. The overall layout of the model is shown in Fig.2. During training the model learns both an anatomical model and how to warp and render this anatomy to achieve accurate reconstruction of input volumes. Once trained random deformations and renderings can be sampled to generate synthetic volumes.The anatomical model is a fixed size multi-channel 3D volume the values of which are learnt during training. This can be understood as learning a canonical “template” (Fig.3). In each voxel the values across the channels sum to one, thus each channel can be seen as representing a particular tissue, with the values representing the proportion of each tissue type in the voxel. These semantics are also encouraged by the renderer (see below) which assigns one intensity value to each channel.
The variational encoder-decoder (VED) networks are used to learn generative models over the warping and rendering parameters during training. They can be understood as variational auto-encoders6 embedded within the larger model.
The transform network performs both linear and non-linear deformations of the learns anatomical model. This network is essentially a spatial transformer network7, which takes the anatomical model and transformation parameters as input, and yields the warped model.
The final step is to convert the warped anatomical model into an image. We refer to this step as ‘rendering’. In order to encourage the anatomical model to capture as much information as possible we restrict the renderer to a simple network that assigns a single colour (i.e. intensity) per tissue. However, this enforced simplicity also results in degraded synthetic images, and thus after training this model we then train a state-of-the-art mask-conditioned generative model5 using the learned anatomical model to provide the required dense semantic masks (see below).
For our experiments we use the ACDC dataset8, which consists of multi-slice cardiac MR images of 100 patients (both healthy and unhealthy). We resample the images to1.3×1.3mm2 in-plane resolution and crop to 144×144 pixels. In total we have 200 (100 end-systolic, 100 end-diastolic) volumes, each with an average of 9 slices. We augment this data (and ensure a standard input size) by generating random 128×128 pixel 8-slice sub volumes. We train the proposed model (using Adam9 with default parameters) to minimise reconstruction error and penalty terms regularising the VEDs and transformer network. We then use the model to generate dense segmentation masks for each training volume. This provides a dense semantic mask for every slice in the dataset (approx 1800 images). We use this set of image-mask pairs to train a state-of-the-art mask conditioned image synthesis model5, which produces our final synthetic results.
Results
Given Gaussian noise as input, the learnt model synthesises coherent 3D volumes we visualise two example volumes in Fig.4. As can be seen, the data is anatomically coherent both within and between slices, and the synthetic data is not simply memorised from the training set. Further, it can be seen from Fig.5. that the method learns a coherent 3D anatomical model without supervision. It can also be seen from the slices shown in Fig.1. that the model is capable og generating synthetic data with diverse anatomy.Discussion and Conclusion
The proposed model demonstrates that shared underlying morphological structure in the data can be effectively leveraged by enforcing data synthesis through a shared anatomical model. We also believe that the model benefits from emulating the real factored nature of medical image generation into patient (anatomical model) and image acquisition (rendering). Also, as the proposed model is not cardiac specific and it can thus be applied directly to MR images of other anatomy. Currently, our method uses a voxelised anatomical model. However, future work looking instead at learning continuous (e.g. mesh-based) anatomy would open up a number of research directions, for example using the learned models in biomechanical simulations. Additionally, including known physical constrains in the rendering process (moving towards simulating full MRI acquisition and reconstruction) is another potentially rich avenue of investigation.Acknowledgements
No acknowledgement found.References
- Xin Yi, Ekta Walia, and Paul Babyn. Generative adversarial network in medical imaging: A review.arXiv preprint arXiv:1809.07294, 2018.
- Agisilaos Chartsias, Thomas Joyce, Rohan Dharmakumar, and Sotirios A Tsaftaris. Adversarial image synthesis for unpaired multi-modal cardiac data. In International Workshop on Simulation and Synthesis in Medical Imaging.
- Maayan Frid-Adar, Idit Diamant, Eyal Klang, Michal Amitai, Jacob Goldberger, and Hayit Greenspan. Gan-based synthetic medical image augmentation for increased CNN performance in liver lesion classification. Neurocomputing, 321:321–331, 2018.
- Tran Minh Quan, Thanh Nguyen-Duc, and Won-Ki Jeong. Compressed sensing MRI reconstruction using a generative adversarial network with a cyclic loss. IEEE transactions on medical imaging, 37(6):1488–1497, 2018.
- Taesung Park, Ming-Yu Liu, Ting-Chun Wang, and Jun-Yan Zhu. Semantic image synthesis with spatially-adaptive normalization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2019.
- Diederik P Kingma and Max Welling. Auto-encoding variational bayes. arXiv preprint arXiv:1312.6114, 2013.
- Jaderberg, Max, Karen Simonyan, and Andrew Zisserman. "Spatial transformer networks." In Advances in neural information processing systems, pp. 2017-2025. 2015.
- Olivier Bernard, Alain Lalande, Clement Zotti, Frederick Cervenansky, Xin Yang,Pheng-Ann Heng, Irem Cetin, Karim Lekadir, Oscar Camara, Miguel Angel Gonzalez Ballester, et al. Deep learning techniques for automatic mri cardiac multi-structuressegmentation and diagnosis: Is the problem solved? IEEE transactions on medicalimaging, 37(11):2514–2525, 2018.
- Kingma, Diederik P., and Jimmy Ba. Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980, 2014.
Figures
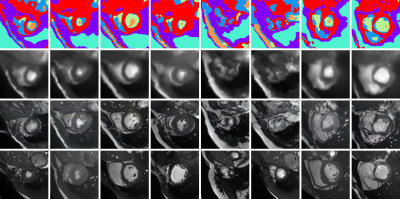
Example synthetic cardiac MR images from the proposed model. The first row shows random samples from the learnt multi-tissue anatomical model, the second and third rows show synthetic images generated conditioned on those anatomical model samples with the simple and state-of-the-art renderer5 respectively. The final row shows the closest (L2-norm) real image in the (augmented) training set. (Note that the model synthesises 3D volumes and we visualise random slices).

An overview of the proposed approach. During training (left) the anatomical model, encoder and decoder networks are learnt through self-supervision. Image volumes are encoded to latent vectors zt (encoding the transformation) and zr (encoding the rendering), which are both encouraged to have a Gaussian distribution. When synthesising data (right) Gaussian noise is fed to the decoders, and a synthetic volume is produced by realistically deforming and rendering the learnt anatomical model.

Example of a learnt anatomical model. The model was learnt with six tissue types and then clustered into six classes for visualisation with one colour per class. The base to apical slices are shown from left to right. It can be seen that, although learnt without supervision, various anatomical parts are clearly visible, such as the ventricular cavities, the myocardium and the chest wall.
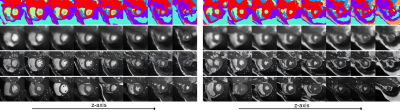
Two example 3D synthetic image sets (128x128x8 voxels). Each 3D image consist of 8 short-axis slices. The first three rows show the sampled anatomical model, result of the simple renderer, and result of the state-of-the-art renderer5. The final row shows, for each generated slice, the most similar slice (L2-norm) from the (augmented) training set.