0742
Measuring the full diffusional intra- and inter-compartmental kurtosis tensors using double diffusion encoding1Champalimaud Research, Champalimaud Centre for the Unknown, Lisbon, Portugal, 2Center of Functionally Integrative Neuroscience (CFIN) and MINDLab, Clinical Institute, Aarhus University, Aarhus, Denmark, 3Department of Physics and Astronomy, Aarhus University, Aarhus, Denmark
Synopsis
Diffusional kurtosis imaging (DKI) quantifies the non-Gaussian degree of diffusion using the kurtosis tensor. However, kurtosis can depend on conflicting sources of non-Gaussian diffusion such as Gaussian diffusion variance (inter-compartmental kurtosis) or the presence of restricted and hindered effects inside compartments (intra-compartmental kurtosis). Here, we develop and apply a novel double diffusion encoding method that is capable of providing the full directional dependence of both inter- and intra-compartmental kurtosis which can be summarized into two distinct kurtosis tensors and thereby improving kurtosis specificity and potentially providing information for diffusion model validation.
Introduction
Diffusional kurtosis imaging (DKI) quantifies the non-Gaussian diffusion, and its full directional dependence1, from data acquired using conventional Single Diffusion Encoding (SDE)2,3. The kurtosis tensor provides numerous rotationally invariant metrics which are typically highly valuable for better characterization of microstructure in many applications4,5, and for better tractography6,7. Nevertheless, for each gradient direction, kurtosis estimates depend on conflicting sources of non-Gaussian diffusion such as (1)polydispersity in apparent diffusivities (inter-compartmental kurtosis, $$$K^{inter}$$$)8-11; and (2) the presence of restricted and hindered diffusion effects inside compartments (intra-compartment kurtosis $$$K^{intra}$$$)10-16. Resolving these kurtosis contributions could significantly enhance DKI’s specificity and assist in validating microstructural models17,18. In this study, we theoretically show that the full directional dependence of both $$$K^{inter}$$$ and $$$K^{intra}$$$ can be resolved using double diffusion encoding (DDE)3,14,18-24. This information can then be combined into distinct 4th-order tensors which can be used to extract measures specific to inter- and intra-compartmental kurtosis sources. Our theory is tested in simulations and used to infer the direction dependence of $$$K^{inter}$$$ and $$$K^{intra}$$$ in data of an ex vivo mouse brain.Theory
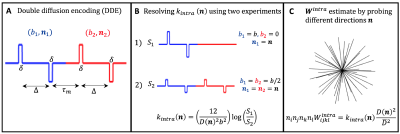
Directional kurtosis estimates: For tissues comprising multiple non-exchanging compartments, characterized by individual diffusivities $$$D_c(\mathbf{n})$$$ and excess-kurtoses $$$K_c(\mathbf{n})$$$, the signal measured from DDE (Fig.1A) with parallel gradient directions ($$$\mathbf{n}_1=\mathbf{n}_2=\mathbf{n}$$$) can expressed as (long mixing time approximation)11,14,15,19:$$\log{S(b_1,b_2,\mathbf{n})}=\log\left\langle\exp\left[-\left(b_{1}+b_{2}\right)D_c(\mathbf{n})+\frac{1}{6}\left(b_{1}^2+b_{2}^2\right)D_c^2(\mathbf{n})K_c(\mathbf{n})+O(b^3)) \right] \right\rangle$$(Eq.1)
where $$$b_1$$$ and $$$b_2$$$ are the b-values of the two diffusion gradients applied and $$$\left\langle...\right\rangle$$$ represents the average across different compartments. Eq.1 can be approximated up to the second order in $$$b$$$ by:
$$\log{S(b_1,b_2,\mathbf{n})}=-\left(b_{1}+b_{2}\right)D(\mathbf{n})+\frac{1}{6}\left(b_{1}+b_{2}\right)^2D^2(\mathbf{n})K^{inter}(\mathbf{n})$$
$$+\frac{1}{6}\left(b_{1}^2+b_{2}^2\right)D^2(\mathbf{n})K^{intra}(\mathbf{n})$$(Eq.2)
where $$$D(\mathbf{n})$$$, $$$K^{inter}(\mathbf{n})$$$ and $$$K^{intra}(\mathbf{n})$$$ are the total directional diffusivity, and total inter- and intra-compartmental kurtosis:
$$D(\mathbf{n})=\left\langle D_c(\mathbf{n})\right\rangle,$$
$$K^{inter}(\mathbf{n})=3\frac{\left ( \left\langle D_c(\mathbf{n})\right\rangle^2-\left\langle D_c(\mathbf{n})\right\rangle^2\right )}{D^2(\mathbf{n})},$$
$$K^{intra}(\mathbf{n})=\frac{\left\langle D_c^2(\mathbf{n})K_c(\mathbf{n})\right\rangle}{D^2(\mathbf{n})}$$(Eq.3)
From Eq.2, $$$K^{intra}(\mathbf{n})$$$ can be extracted using two DDE experiments with constant total b-value=$$$b=b_1+b_2$$$ (Fig.1B):
$$K^{intra}(\mathbf{n})=\frac{12}{D^2(\mathbf{n})b^2}\left(\log{S(b,0,\mathbf{n})}-\log{S(b/2,b/2,\mathbf{n})}\right)$$(Eq.4)
Inter– and intra-compartmental kurtosis tensors: If the above DDE experiments are repeated for different directions $$$\mathbf{n}$$$ and different b-values=$$$b$$$, $$$K^{intra}(\mathbf{n})$$$ estimates can be used to reconstruct the full intra-compartmental kurtosis tensor $$$n_in_jn_kn_lW^{intra}_{ijkl}=K^{intra}(\mathbf{n})D^2(\mathbf{n})/\overline{D}^2$$$, where $$$\overline{D}=$$$ mean diffusivity (Fig1.C). Alternatively, $$$\mathbf{W}^{intra}$$$, together with the inter-compartmental tensor $$$\mathbf{W}^{inter}$$$, can be incorporated to Eq.2 and fitted from $$$S(b,0,\mathbf{n})$$$ and $$$S(b/2,b/2,\mathbf{n})$$$ signals acquired for different $$$\mathbf{n}$$$ and b-values=$$$b$$$:
$$\log{S(b_1,b_2,\mathbf{n})}=-\left(b_{1}+b_{2}\right)D(\mathbf{n})+\frac{1}{6}\left(b_{1}+b_{2}\right)^2\overline{D}^2n_in_jn_kn_lW^{inter}_{ijkl}+$$
$$\frac{1}{6}\left(b_{1}^2+b_{2}^2\right)\overline{D}^2n_in_jn_kn_lW^{intra}_{ijkl}$$(Eq.5)
kurtosis metrics: All measures previously defined for DKI’s total kurtosis tensor $$$\mathbf{W}$$$ are applicable to $$$\mathbf{W}^{inter}$$$ and $$$\mathbf{W}^{intra}$$$, e.g. axial and radial kurtosis (AK and RK)1,7,11. Additionaly, to remove the dependence of tissue organization16,25, one can compute scalar kurtosis estimates ($$$\overline{K}^{inter}$$$ and $$$\overline{K}^{intra}$$$) from directionally averaged (i.e., powder-averaged) signals $$$\overline{S}(b_1,b_2)=\sum_iS(b_1,b_2,\mathbf{n}^i)$$$).
Methods
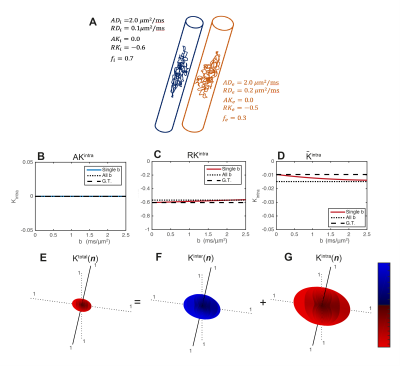
- Simulations. Synthetic signals are produced for two restricted infinite cylinders of different radius (i.e., different RD and RK values), Fig.2A. For these simulations $$$K^{intra}(\mathbf{n})$$$ is estimated for axial and radial directions and for powder-averaged signals at different b-values=b (from 0 to 2.5ms/μm2). $$$\mathbf{W}^{inter}$$$ and $$$\mathbf{W}^{intra}$$$ are then fitted to all these signals simultaneously.
- Tissue extraction. Animal experiments were preapproved by the competent institutional and national authorities (European Directive 2010/63). A C57BL/6J mice brain (13 weeks) was transcardially perfused, immersed in 4% Paraformaldehyde (PFA) solution (24h), washed in Phosphate-Buffered Saline (PBS) solution (48h) and placed in a 10mm NMR tube with Fluorinert.
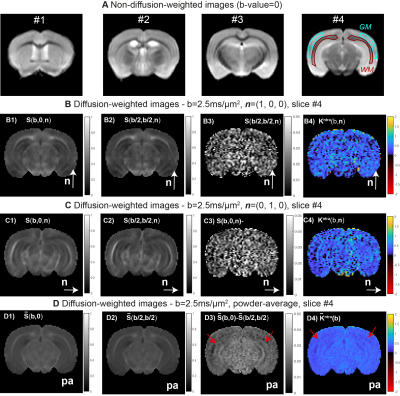
- MRI Experiments. MRI scans were performed at 37oC using a 16.4 T Aeon Bruker scanner equipped with a Micro5 probe (which produces gradients up to 3000 mT/m). DDE data were acquired for $$$S(b, 0,\mathbf{n})$$$ and $$$S(b/2,b/2,\mathbf{n})$$$ experiments (Fig1.B) for b=[0,1.00,1.25,1.50,2.00,2.5ms/μm2] and for the 45 directions (Fig1.C). Other acquisition parameters are set to:Δ=τm=13ms, δ=1.5ms; TR/TE=2200/52ms, resolution=130×130x900μm3, partial Fourier acceleration=1.42. $$$K_{intra}$$$ is first analysed separately for each b-value repetition, then $$$\mathbf{W}^{inter}$$$ and $$$\mathbf{W}^{intra}$$$ and respective invarianted are extracted from all acquired data.
Results and Discussion
- Simulations: Radial $$$K^{intra}$$$ and $$$\overline{K}^{intra}$$$ estimates detect the expected negative intra-compartmental kurtosis effects of restricted cylinders (Fig.2C-D). The directional dependence of $$$\mathbf{W}$$$, $$$\mathbf{W}^{inter}$$$ and $$$\mathbf{W}^{intra}$$$ is presented in Fig.2E-G. The $$$\mathbf{W}^{inter}$$$ and $$$\mathbf{W}^{intra}$$$ decouples the positive non-Gaussian effects of diffusion variance across compartments (Fig.2F) from negative non-Gaussian effects of restricted diffusion (Fig.2G).
- MRI experiments: WM and GM ROIs placed at b=0 images revealed SNRs=70±20 and 110±10 (Fig.3A). For a representative slice and b=2.5ms/μm2, the $$$S(b, 0,\mathbf{n})$$$ and $$$S(b/2,b/2,\mathbf{n})$$$ estimates for $$$\mathbf{n}=[1,0,0]$$$ and $$$\mathbf{n}=[0,1,0]$$$ are displayed in Fig.3B-C, while powder-averaged $$$\overline{S}(b,0)$$$ and $$$\overline{S}(b/2,b/2)$$$ signal are shown in Fig.3D. The differences between these maps reveals that $$$S(b, 0,\mathbf{n})$$$ is generally higher than $$$S(b/2, b/2,\mathbf{n})$$$ (Fig.3B3, Fig.3C3, and Fig.3D3)), which indicates positive intra-compartmental kurtosis values for both GM and WM (Fig.3B4, Fig.3C4, and Fig.3D4). Visually the $$$K^{intra}(\mathbf{n})$$$ estimates for individual directions present low precision; however, results from powder-averaged $$$\overline{K}^{intra}$$$ estimates indicates that intra-compartmental kurtosis effects are lower in WM (red arrow in Fig. 3D4).
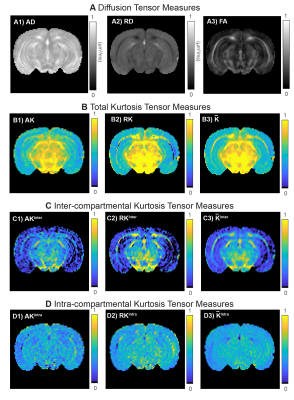
Fig.4 shows metrics extracted from different tensors. As expected the total RK is higher than the total AK in WM (Fig.4B) which is revealed to be mainly caused by high RKinter values (Fig.4C2). Both AK and RK maps reveal that intra-compartmental kurtosis is the highest source in GM.
Conclusions and future work
We show that $$$\mathbf{W}^{inter}$$$ and $$$\mathbf{W}^{intra}$$$ can be extracted from DDE data acquired with parallel gradient direction pairs and constant total b-values. In future studies, this methodology will be further explored to assess and improve its robustness to noise and artefacts. We also intend to further explore and validate the positive intra-compartmental observed on WM and GM regions.Acknowledgements
This study was funded by the European Research Council (ERC) (agreement No. 679058).References
1. Jensen JH, Helpern JA, Ramani A, et al. Diffusional Kurtosis Imaging: The Quantification of Non-Gaussian Water Diffusion by Means of Magnetic Resonance Imaging, Magn. Reson. Med. 2005; 53: 1432–1440
2.Stejskal EO, Tanner JE. Spin Diffusion Measurements: Spin Echoes in the Presence of a Time-Dependent Field Gradient. The Journal of Chemical Physics 1965; 42(1): 288-292. doi:10.1063/1.1695690
3. Shemesh N, Jespersen SN, Alexander DC, et al.. Conventions and nomenclature for double diffusion encoding NMR and MRI. Magn. Reson. Med. 2016: 75: 82–87. doi:10.1002/mrm.25901
4. Cheung JS, Wang E, Lo EH, Sun PZ. Stratification of heterogeneous diffusion MRI ischemic lesion with kurtosis imaging: evaluation of mean diffusion and kurtosis MRI mismatch in an animal model of transient focal ischemia. Stroke 2012; 43: 2252–4. doi: 10.1161/STROKEAHA.112.661926
5. Falangola MF, Jensen JH, Babb JS, et al. Age-related non-Gaussian diffusion patterns in the prefrontal brain. J. Magn. Reson. Imaging 2008; 28: 1345–1350. doi:10.1002/jmri.21604
6. Jensen JH, Helpern JA, Tabesh A. Leading non-Gaussian corrections for diffusion orientation distribution function. NMR Biomed. 2014; 27: 202-211. doi: 10.1002/nbm.3053
7. Henriques RN, Correia MM, Nunes RG, Ferreira HA. Exploring the 3D Geometry of the Diffusion Kurtosis Tensor - Impacts on the Development of Robust Tractography Procedures and Novel Biomarkers. Neuroimage 2015; 111:85-99. doi.: 10.1016/j.neuroimage. 2015.02.004
8. Assaf Y, Cohen Y. Non‐mono‐exponential attenuation of water and N‐acetyl aspartate signals due to diffusion in brain tissue. J Magn Reson. 1998;131:69–85.
9. Yablonskiy DA, Bretthorst GL, Ackerman JJ. Statistical model for diffusion attenuated MR signal. Magn Reson Med. 2003;50:664–669.
10. Jensen JH, Helpern JA. MRI quantification of non‐Gaussian water diffusion by kurtosis analysis. NMR Biomed. 2010;23:698–710.
11. Jespersen, White Matter biomarkers from diffusion MRI. J. Magn. Reson. Imaging 2018; 291: 127–140. doi: 10.1016/j.jmr.2018.03.001
12. Callaghan PT, Coy A, MacGowan D, et al. Diffraction‐like effects in NMR diffusion studies of fluids in porous solids. Nature. 1991;351:467–469.
13. van Gelderen P, DesPres D, van Zijl PC, Moonen CT. Evaluation of restricted diffusion in cylinders: Phosphocreatine in rabbit leg muscle. J Magn Reson B. 1994;103:255–260.
14. Paulsen JL, Özarslan E, Komlosh ME et al. Detecting compartmental non-Gaussian diffusion with symmetrized double-PFG MRI. NMR Biomed. 2015; 28: 1550-6. doi: 10.1002/nbm.3363
15. Dhital B, Kellner E, Kiselev VG, Reisert M. The absence of restricted water pool in brain white matter. Neuroimage 2018; 182: 398-406. doi:10.1016/j.neuroimage.2017.10.051
16. Henriques RN, Jespersen SN, Shemesh N. Microscopic anisotropy misestimation in spherical‐mean single diffusion encoding MRI. Magn Reson Med. 2019; 81(5):3245-3261. doi: 10.1002/mrm.27606.
17. Lampinen B, Szczepankiewicz F, Mårtensson J, et al. Neurite density imaging versus imaging of microscopic anisotropy in diffu- sion MRI: A model comparison using spherical tensor encoding. Neuroimage. 2017;147:517–531.
18. Mitra PP. Multiple wave-vector extensions of the NMR pulsed-field-gradient spin-echo diffusion measurement. Phys. Rev. B 1995; 51: 15074– 15078. doi: 10.1103/PhysRevB.51.15074
19. Jespersen SN. Equivalence of double and single wave vector diffusion contrast at low diffusion weighting. NMR in Biomed. 2011; 25(6): 813-818. doi: 10.1002/nbm.1808.
20. Jespersen SN, Lundell H, Sønderby CK, Dyrby TB. Orientationally invariant metrics of apparent compartment eccentricity from double pulsed field gradient diffusion experiments. NMR Biomed. 2013; 26(12):1647-62. doi: 10.1002/nbm.2999.
21. Jespersen SN, Buhl N. The displacement correlation tensor: Microstructure, ensemble anisotropy and curving fibers. J. Magn. Reson. 2011; 208: 34–43.doi: 10.1016/j.jmr.2010.10.003.
22. Koch MA, Finsterbush J. Compartment size estimation with double wave vector diffusion-weighted imaging. Magn. Reson. Med. 2008; 60(1); 90- 101. doi:10.1002/mrm.21514
23. Özarslan E. Compartment shape anisotropy (CSA) revealed by double pulsed field gradient MR. J Magn Reson. 2009;199: 56–67.
24. Jensen JH, Hui ES, Helpern JA. Double-pulsed diffusional kurtosis imaging. NMR Biomed. 2014; 27:363-370. doi: 10.1002/nbm.3094
25. Kaden E, Kruggel F, Alexander DC. Quantitative mapping of the per‐axon diffusion coefficients in brain white matter. Magn Reson Med. 2016;75:1752–1763.
Figures