0741
Towards Clinical Translation of Microscopic Diffusion Spectrum Imaging1Centre for Medical Image Computing, University College London, London, United Kingdom, 2Great Ormond Street Institute of Child Health, University College London, London, United Kingdom, 3Siemens Healthcare Ltd, Frimley, United Kingdom
Synopsis
Conventional wisdom suggests that it is necessary to average the diffusion signal over the gradient directions to map microstructural features in the presence of orientational heterogeneity. Contrary to this belief, we show that powder-averaging the signal is redundant and leverage this insight to perform, within the same scan time, diffusion experiments with many rather than few b-values and with many rather than few gradient waveforms for b-tensor encoding and beyond, facilitating the translation of advanced techniques such as microscopic diffusion spectrum imaging to clinical practice.
Introduction
Microscopic diffusion anisotropy mapping has enabled us to recover microstructural parameters not confounded by fibre crossings and orientation dispersion. Whether the Spherical Mean Technique1,2, double diffusion encoding3,4 or b-tensor measurements5,6, we typically acquire a few b-shells with evenly distributed gradient directions and, to regress out unwanted orientation effects, employ the powder-averaged signal over the gradient directions to detect microscopic tissue structure. This approach, however, is limited to simple diffusion models since the acquisition of many b-values and gradient waveforms, as required by advanced techniques, is not achievable within clinically viable scan times.Methods
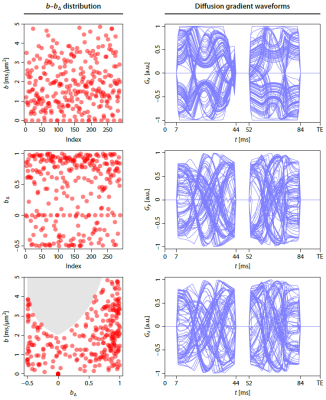
Powder-averaging is redundant. The key insight is that there is no need for prior averaging of the diffusion signal over the gradient directions to factor out orientation effects. Indeed, it can be shown that we may measure the diffusion gradients and gradient waveforms in an arbitrary way as long as the directional encoding is uniform. The algorithm reads:1. Perform a diffusion scan that covers a wide range of b-values and gradient waveforms, ensuring that the gradient directions are evenly distributed.
2. Devise a diffusion model, whether signal representation or biophysically motivated, and compute its powder-average, i.e. the integral over the gradient directions.
3. Fit the powder-averaged model to the measurements without averaging the diffusion signal over the gradient directions.
This approach allows us to sample the measurement space more efficiently, yet removes confounding orientation effects without prior assumptions.
Experiment design. We developed a bespoke diffusion-weighted spin-echo EPI sequence that enables measurements with arbitrary gradient waveforms in each TR period. A pilot study with a healthy volunteer was performed on a 3T Siemens Prisma scanner after written informed consent. We acquired 270 b-tensor encoding measurements with randomly sampled b-values, shapes bΔ and gradient directions (Figure 1). The gradient waveforms were optimised7 and compensated for Maxwell terms8, assuming that time dependence effects are negligible9. The other sequence parameters (TR=9.5 s, TE=96 ms, 1.7 mm isotropic, GRAPPA/2, measured twice with reversed EPI readout directions) were fixed. Additionally, we acquired a second dataset at 2 mm isotropic resolution that is achievable within practical scan times if used with multiband acceleration10.
Microscopic diffusion spectrum imaging. To demonstrate the benefit of rich b–bΔ data sampling, we study an advanced diffusion method11,12 that has been prohibitive for clinical use so far. Let us consider a microdomain population model formed of a distribution of microscopic diffusion tensors that are axially symmetric and have unknown orientations. λ1 and λ2 denote the parallel and perpendicular microscopic diffusivities, respectively. The powder-averaged signal takes the form13
$$\frac{\bar E(b,b_\Delta)}{E_0}=\iint_\Lambda\bar h(b,b_\Delta;\lambda_1,\lambda_2)\,p(\lambda_1, \lambda_2)\,d\lambda_1d\lambda_2$$
with
$$\bar h(b,b_\Delta;\lambda_1,\lambda_2)=\exp\left(-b\left[\frac{1-b_\Delta}{3}\lambda_1+\frac{2+b_\Delta}{3}\lambda_2 \right]\right){}_1F_1(1/2,3/2,-bb_\Delta[\lambda_1-\lambda_2]).$$
This work aims to estimate, irrespective of the tensor orientation distribution, the two-dimensional distribution p(λ1, λ2) of microscopic diffusivities, also referred to as microscopic diffusion spectrum, where $$$\Lambda=\{(\lambda_1,\lambda_2)\colon\lambda_1,\lambda_2\in [0,\lambda_\mathrm{free}],\lambda_1\geq\lambda_2 \}$$$ and λfree is the diffusion coefficient of free water at 37 °C.
Deep-learning spectrum fitting. For the fast and robust estimation of the 2D microscopic diffusion spectrum in the presence of orientational heterogeneity, we use a neural network of three fully connected layers with rectified linear unit and, in the last layer, softmax activation functions14 which guarantees by design the characteristic properties of the spectrum, i.e. non-negativity and normalisation to unity. The network is trained, exploiting the redundancy of signal powder-averaging, with 100 billion synthetic spectra drawn from a Dirichlet process mixture using a Kullback–Leibler divergence loss criterion and a multi-resolution approach with a stochastic gradient descent optimiser.
Results
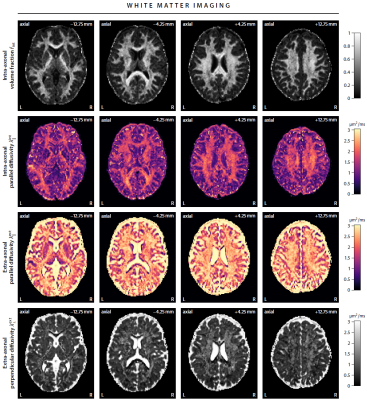
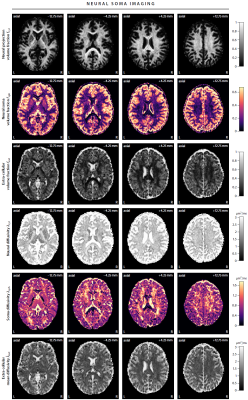
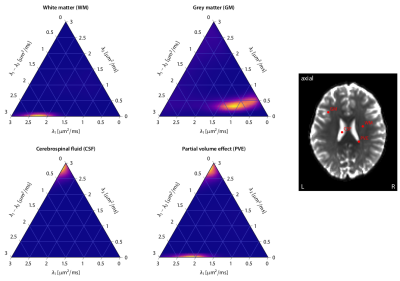
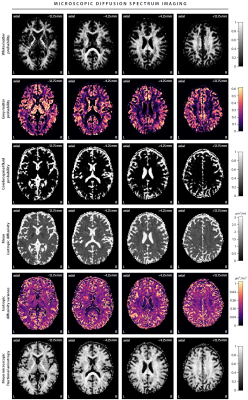
First, we demonstrate the new framework in two advanced biophysical models. Figure 2 shows the unconstrained estimation of a two-compartment white matter model15,16. The confounding orientation effects have been factored out. Grey matter tissue features a more heterogeneous microarchitecture which is addressed by Neural Soma Imaging17, a recently proposed three-compartment model shown in Figure 3. No spatial regularisation or prior denoising have been applied. Next, we demonstrate two-dimensional microscopic diffusion spectrum imaging. Figure 4 illustrates four example spectra estimated on a 40×40-grid, enabling the detailed analysis of microscopic anisotropy and diffusional heterogeneity. Summary maps of microscopic diffusion spectra are displayed in Figure 5. For instance, we may calculate the probability that the microscopic diffusivities are in a range that is representative for a certain tissue type or pathological condition. A noteworthy result is that the variance of isotropic diffusivity is lower in white matter, providing further evidence that the cell morphology is more heterogeneous in grey matter due to the abundance of neural projections and soma. We obtain similar results for the dataset with 2 mm isotropic resolution (not shown).Discussion
In this work we have developed a microstructural imaging technique that makes explicit averaging of the diffusion signal over the gradient directions redundant and at the same time regresses out the confounding effects of fibre crossings and orientation dispersion. The gain of measuring a multitude of b-values and gradient waveforms is demonstrated in microscopic diffusion spectrum mapping (Figures 4 and 5). The general idea extends naturally to more advanced experiment designs and diffusion models. The scan time is less than 12 min using multiband EPI10, and deep-learning parameter fitting provides the results within seconds, which facilitates the routine use of microscopic diffusion spectrum imaging in the clinic.Acknowledgements
This research received support from UK EPSRC EP/M020533/1, EP/N018702/1 and EU H2020 634541-2. NGG thanks the London Interdisciplinary Doctoral Programme (UK BBSRC BB/M009513/1). This work was supported by the UK NIHR GOSH Biomedical Research Centre. The software is available online at https://ekaden.github.io.References
1. E. Kaden, F. Kruggel, and D. C. Alexander. Quantitative mapping of the per-axon diffusion coefficients in brain white matter. Magnetic Resonance in Medicine, 75:1752–1763, 2016.
2. E. Kaden, N. D. Kelm, R. P. Carson, M. D. Does, and D. C. Alexander. Multi-compartment microscopic diffusion imaging. NeuroImage, 139:346–359, 2016.
3. M. Lawrenz, M. A. Koch, and J. Finsterbusch. A tensor model and measures of microscopic anisotropy for double-wave-vector diffusion-weighting experiments with long mixing times. Journal of Magnetic Resonance, 202:43–56, 2010.
4. S. N. Jespersen, H. Lundell, C. K. Sonderby, and T. B. Dyrby. Orientationally invariant metrics of apparent compartment eccentricity from double pulsed field gradient diffusion experiments. NMR in Biomedicine, 26:1647–1662, 2013.
5. S. Lasic, F. Szczepankiewicz, S. Eriksson, M. Nilsson, and D. Topgaard. Microanisotropy imaging: quantification of microscopic diffusion anisotropy and orientational order parameter by diffusion MRI with magic-angle spinning of the q-vector. Frontiers in Physics, 2(11), 2014.
6. C.-F. Westin, H. Knutsson, O. Pasternak, F. Szczepankiewicz, E. Ozarslan, D. van Westen, C. Mattisson, M. Bogren, L. J. O’Donnell, M. Kubicki, D. Topgaard, and M. Nilsson. Q-space trajectory imaging for multidimensional diffusion MRI of the human brain. NeuroImage, 135:345–362, 2016.
7. J. Sjolund, F. Szczepankiewicz, M. Nilsson, D. Topgaard, C.-F. Westin, and H. Knutsson. Constrained optimization of gradient waveforms for generalized diffusion encoding. Journal of Magnetic Resonance, 261:157–168, 2015.
8. F. Szczepankiewicz, C.-F. Westin, and M. Nilsson. Maxwell-compensated design of asymmetric gradient waveforms for tensor-valued diffusion encoding. Magnetic Resonance in Medicine, 82:1424–1437, 2019.
9. N. G. Gyori, K. K. Seunarine, M. G. Hall, C. A. Clark, D. C. Alexander, and E. Kaden. Time dependence in b-tensor encoding. In Proceedings of the 27th Annual Meeting of the ISMRM, page 3549, 2019.
10. K. Setsompop, B. A. Gagoski, J. R. Polimeni, T. Witzel, V. J. Wedeen, and L. L. Wald. Blipped-controlled aliasing in parallel imaging for simultaneous multislice echo planer imaging with reduced g-factor penalty. Magnetic Resonance in Medicine, 67:1210–1224, 2012.
11. J. P. de Almeida Martins and D. Topgaard. Multidimensional correlation of nuclear relaxation rates and diffusion tensors for model-free investigations of heterogeneous anisotropic porous materials. Scientific Reports, 8:2488, 2018.
12. C. M. W. Tax, J. P. de Almeida Martins, F. Szczepankiewicz, C.-F.Westin, M. Chamberland, D. Topgaard, and D. K. Jones. From physical chemistry to human brain biology: unconstrained inversion of 5-dimensional diffusion-T2 correlation data. In Proceedings of the 26th Annual Meeting ISMRM, page 1101, 2018.
13. S. Eriksson, S. Lasic, M. Nilsson, C.-F. Westin, and D. Topgaard. NMR diffusion-encoding with axial symmetry and variable anisotropy: Distinguishing between prolate and oblate microscopic diffusion tensors with unknown orientation distribution. The Journal of Chemical Physics, 142:104201, 2015.
14. I. Goodfellow, Y. Bengio, and A. Courville. Deep Learning. MIT Press, 2016.
15. D. S. Novikov, J. Veraart, I. O. Jelescu, and E. Fieremans. Rotationally-invariant mapping of scalar and orientational metrics of neuronal microstructure with diffusion MRI. NeuroImage, 174:518–538, 2018.
16. E. Fieremans, J. Veraart, B. Ades-Aron, F. Szczepankiewicz, M. Nilsson, and D. S. Novikov. Effect of combining linear with spherical tensor encoding on estimating brain microstructural parameters. In Proceedings of the 26th Annual Meeting of the ISMRM, page 0254, 2018.
17. N. G. Gyori, C. A. Clark, I. Dragonu, D. C. Alexander, and E. Kaden. In-vivo neural soma imaging using b-tensor encoding and deep learning. In Proceedings of the 27th Annual Meeting of the ISMRM, page 0059, 2019.
Figures