0736
Tortuosity assumption not the cause of NODDI’s incompatibility with tensor-valued diffusion encoding
Michele Guerreri1, Filip Szczepankiewicz2,3, Björn Lampinen4, Marco Palombo1, Markus Nilsson2, and Hui Zhang1
1Computer Science & Centre for Medical Image Computing, University College London, London, United Kingdom, 2Clinical Sciences Lund, Department of Radiology, Lund University, Lund, Sweden, 3Radiology, Brigham and Women’s Hospital, Harvard Medical School, Boston, MA, United States, 4Clinical Sciences Lund, Department of Medical Radiation Physics, Lund University, Lund, Sweden
1Computer Science & Centre for Medical Image Computing, University College London, London, United Kingdom, 2Clinical Sciences Lund, Department of Radiology, Lund University, Lund, Sweden, 3Radiology, Brigham and Women’s Hospital, Harvard Medical School, Boston, MA, United States, 4Clinical Sciences Lund, Department of Medical Radiation Physics, Lund University, Lund, Sweden
Synopsis
This work shows that the tortuosity assumption in NODDI can not be identified as the source of incompatibility when the model is extended to data acquired with tensor-valued diffusion encoding. NODDI, originally developed for multi-shell linear tensor encoded (LTE) data, was shown to be inadequate when extended to LTE and spherical tensor encoded (STE) data jointly. The adoption of tortuosity assumption by NODDI has been suggested as a plausible explanation. We conduct a systematic model-comparison study to show that this explanation is inaccurate. We identify a different assumption of the model, the equal-axial-diffusivity, as a source of incompatibility.
Introduction
We present a model-comparison study aimed at clarifying which of NODDI’s constraints may be identified as the main source of incompatibility, when the model is fitted to data acquired with tensor-valued diffusion encoding. NODDI is a biophysical model designed for inferring various indices of neurite morphology from conventional multi-shell dMRI data1. It relies on a set of constraints which are imposed to ensure robust parameter estimation (Figure 1). Recently NODDI has been shown to be incompatible with a new class of data2 from tensor-valued diffusion encoding3,4, calling into question the validity of its assumptions. Lampinen et al. suggested this incompatibility is induced by NODDI’s tortuosity constraint2,5. This work shows that NODDI’s inconsistency is not caused by the tortuosity assumption, rather it is induced by another constraint of the model, namely the equal-axial-diffusivity6-9. The resulting incompatibility is worsened by having the value of the axial diffusivity fixed, which is required for fitting the model to conventional dMRI data only.Methods
MODELLING
The key question we want to answer is which NODDI constraints are responsible for the observed incompatibilities. As we mentioned, Lampinen et al. suggested NODDI’s tortuosity constraint is responsible for this incompatibility2. The authors proposed CODIVIDE2, which doesn’t adopt tortuosity (figure 1). However, CODIVIDE differs from NODDI in two more aspects: (i) it replaces NODDI’s equal-axial-diffusivity assumption with the equal-isotropic-diffusivity; (ii) it exploits the full potential of tensor-valued diffusion encoding by increasing the number of free parameters, estimating the isotropic diffusivity10. As a consequence, the analysis based on CODIVIDE model can not be used to draw a firm conclusion on the tortuosity role. To clarify this point, we introduce a NODDI variant (named NODDI.a, Figure 1) which differ from CODIVIDE in one way only, namely the adoption of the tortuosity assumption11. NODDI.a is different from the original NODDI by adopting the equal-isotropic-diffusivity2 and by estimating the diffusivity directly from the data2. If the tortuosity is a key source of incompatibility, then NODDI.a should perform worse than CODIVIDE. Furthermore, we assess the effect of the equal-axial-diffusivity assumption, by introducing another variant of NODDI (named NODDI.b, Figure 1). NODDI.b differs from NODDI.a by retaining both equal-axial-diffusivity and tortuosity assumptions. NODDI.b differs from original NODDI by estimating the axial-diffusivity directly from the data. If the equal-axial-diffusivity is a key source of incompatibility, then NODDI.b will perform worse than NODDI.a.
DATA
We use data from three healthy volunteers acquired with both linear tensor encoding (LTE) and spherical tensor encoding (STE) on a 3T MAGNETOM Prisma (Siemens Healthcare GmbH, Erlangen, Germany) with a prototype spin-echo sequence that enables variable tensor-valued diffusion encoding. Imaging parameters were: TR=7s, TE=90ms, resolution 2x2x2mm3, b=(100,500,1000,1500,2000) s/mm2, number of gradient directions=6,10,12,16,20. Gradient waveforms were Maxwell-compensated12 and optimized numerically13.
ANALYSIS
The models are fitted to powder average data14. NODDI.a, NODDI.b, and CODIVIDE are fitted to both LTE and STE data. Original NODDI is fitted to LTE data only. To help identifying overall trends in the microstructure parameter estimates for different brain tissues, the brains are segmented into partitions of gray matter (GM), white matter (WM), using a DTI-based multi-channel approach15.
Results
Figure 2 shows qualitatively that NODDI.a, NODDI.b and CODIVIDE seem to explain the experimental data equally well in both GM and WM regions of interest.Column 1 of Figure 3 confirms that NODDI.a, NODDI.b and CODIVIDE explain the data similarly well over a representative slice, with the sum-of-squared errors (SSE) of fitting, given that the models have the same number of parameters. The figure also shows several instances of the parameter maps. The value of the parameters looks very similar for NODDI.a and CODIVIDE, while substantial differences can be observed between the others.
Figure 4 compares NODDI.a and CODIVIDE quantitatively. The plots in the figure confirm that there are no significant differences in the fitting quality of the two models both in WM and GM.
Figure 5 compares NODDI.a and NODDI.b quantitatively. The two plots in the figure show that NODDI.b performs systematically worse than NODDI.a, especially in GM.
Discussion and Conclusion
We show that the tortuosity constraint does not affect the fitting performance of NODDI.a compared to CODIVIDE. This implies that tortuosity assumption can not be considered as the source of the previously observed incompatibility.We show that the adoption of equal-isotropic-diffusivity constraint in NODDI.a slightly increases the fitting performance compared to NODDI.b. This implies that the equal-axial-diffusivity constraint can be identified as a cause of failure when NODDI is extended to data acquired with multiple b-tensor encoding.
However, the fitting performance of NODDI.b worsens considerably when the axial diffusivity is fixed to the value used in the original NODDI (result not shown), as shown previously16. This suggests that the primary cause of failure is the fixed axial diffusivity value.
While these results demonstrate that the tortuosity assumption is not the cause of the incompatibility observed in Lampinen et al, they are not intended as a validation of the assumption itself. Independent validation, such as histology17, is necessary to assess its biological accuracy.
Acknowledgements
No acknowledgement found.References
1. Zhang, H., Schneider, T., Wheeler-Kingshott, C. A., and Alexander, D. C. (2012). Noddi: practical in vivo neurite orientation dispersion and density imaging of the human brain. Neuroimage, 61(4):1000–1016.2. Lampinen, B., Szczepankiewicz, F., Mårtensson, J., van Westen, D., Sundgren, P. C., and Nilsson, M. (2017). Neurite density imaging versus imaging of microscopic anisotropy in diffusion mri: A model comparison using spherical tensor encoding. NeuroImage, 147:517–531.
3. Westin, C.-F., Knutsson, H., Pasternak, O., Szczepankiewicz, F., Özarslan, E., van Westen, D., Mattisson, C., Bogren, M., O’donnell, L. J., Kubicki, M., et al. (2016). Q-space trajectory imaging for multidimensional diffusion mri of the human brain. Neuroimage, 135:345–362.
4. Topgaard, D. (2017). Multidimensional diffusion mri. Journal of Magnetic Resonance, 275:98–113.
5. Szafer, A., Zhong, J., and Gore, J. C. (1995). Theoretical model for water diffusion in tissues. Magnetic resonance in medicine, 33(5):697–712.
6. Behrens, T. E., Woolrich, M. W., Jenkinson, M., Johansen-Berg, H., Nunes, R. G., Clare, S., Matthews, P. M., Brady, J. M., and Smith, S. M. (2003). Characterization and propagation of uncertainty in diffusion-weighted mr imaging. Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine, 50(5):1077–1088.
7. Alexander, D. C. (2008). A general framework for experiment design in diffusion mri and its application in measuring direct tissue-microstructure features. Magnetic Resonance in Medicine, 60(2):439–448.
8. Alexander, D. C., Hubbard, P. L., Hall, M. G., Moore, E. A., Ptito, M., Parker, G. J., and Dyrby, T. B. (2010). Orientationally invariant indices of axon diameter and density from diffusion mri. Neuroimage, 52(4):1374–1389.
9. Zhang, H., Hubbard, P. L., Parker, G. J., and Alexander, D. C. (2011). Axon diameter mapping in the presence of orientation dispersion with diffusion mri. Neuroimage, 56(3):1301–1315.
10. Szczepankiewicz, F., van Westen, D., Englund, E., Westin, C.-F., Ståhlberg, F., Lätt, J., Sundgren, P. C., and Nilsson, M. (2016b). The link between diffusion mri and tumor heterogeneity: Mapping cell eccentricity and density by diffusional variance decomposition (divide). Neuroimage, 142:522–532.
11. Guerreri, Michele, et al. "Revised NODDI model for diffusion MRI data with multiple b-tensor encodings." International Society for Magnetic Resonance in Medicine, 2018.
12. Szczepankiewicz, F., Westin, C.-F., and Nilsson, M. (2019). Maxwellcompensated design of asymmetric gradient waveforms for tensor-valued diffusion encoding. Magnetic resonance in medicine.
13. Sjölund, J., Szczepankiewicz, F., Nilsson, M., Topgaard, D., Westin, C.-F., and Knutsson, H. (2015). Constrained optimization of gradient waveforms for generalized diffusion encoding. Journal of Magnetic Resonance, 261:157–168.
14. Lampinen, B. et al. Neurite density imaging versus imaging of microscopic anisotropy in diffusion MRI: A model comparison using spherical tensor encoding. NeuroImage 147, 517-531 (2017).
15. Liu, T., Li, H., Wong, K., Tarokh, A., Guo, L., and Wong, S. T. (2007). Brain tissue segmentation based on dti data. NeuroImage, 38(1):114–123.
16. Guerrero, Jose Manuel, et al. "Optimizing the intrinsic parallel diffusivity in NODDI: an extensive empirical evaluation." BioRxiv (2019).
17. Grussu, Francesco, et al. "Neurite dispersion: a new marker of multiple sclerosis spinal cord pathology?." Annals of clinical and translational neurology 4.9 (2017): 663-679.
18. Eriksson, S., Lasič, S., Nilsson, M., Westin, C.-F., and Topgaard, D. (2015). Nmr diffusion-encoding with axial symmetry and variable anisotropy: Distinguishing between prolate and oblate microscopic diffusion tensors with unknown orientation distribution. The Journal of chemical physics, 142(10):104201.
Figures

Figure 1: The model definitions for 1) the original NODDI , 2) NODDI with estimated diffusivity (NODD.b), 3) the NODDI with equal-isotropic diffusivity assumption2 (NOODI.a), and 4) CODIVIDE2. All the models adopt the same parameterization of diffusion tensors18, with dIk and αdk being the isotropic diffusivity and the anisotropy of the k-th diffusion tensor. The signal fraction parameters (νk) are defined according to the original NODDI definition.The models NODDI.a, NODDI.b and CODIVIDE have the same number of free parameters to estimate, one more than the original NODDI.
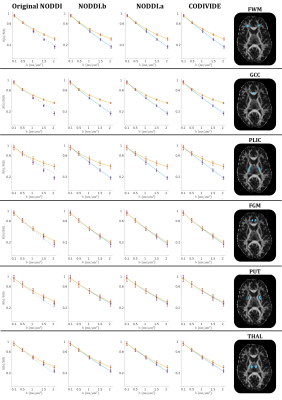
Figure 2:
Qualitative comparison
of data fitting quality. Powder-averaged
signal attenuation is plotted vs b-values in six ROIs from one subject. The data is averaged within each ROI. Orange circles mark the measurements with
linear tensor encoding (LTE); purple squares denote data with spherical tensor
encoding (STE). Vertical bars represent
the standard error of the mean. Solid lines are fitted curves, dashed lines are
predicted curves. GCC - genu of corpus callosum; PLIC - posterior limb of internal capsule; FWM - frontal WM; FGM - frontal
GM; PUT - putamen; THAL - thalamus.
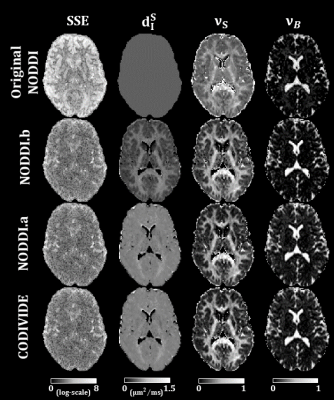
Figure 3:
Maps form original NODDI, NODDI.b, NODDI.a, and
CODIVIDE. The first column shows the maps of the sum-of-squared-errors (SSE) of
fitting the models to the data. The SSE values are log-transformed. We produced
comparable maps for original NODDI, by using its output parameters from LTE to
predict corresponding STE signals. The second column shows maps of the stick
isotropic diffusivity (dIS). The first row of the figure shows original
NODDI’s dIS, which is fixed to 0.56μm2/ms. The
third and fourth columns show maps of the stick fraction (νS) and ball fraction (νB), respectively.
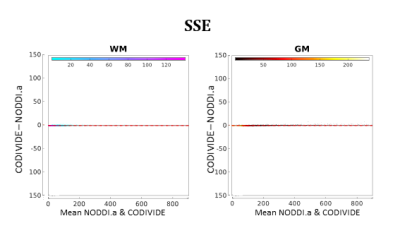
Figure 4:
Bland-Altman plots for quantitative model comparison between NODDI.a and
CODIVIDE, comparing the fit quality with summed squared errors (SSE) of the fit.
Data comes from all three subjects; each point in the plots corresponds to a
single voxel from one of the subjects. The left panel shows voxels of WM (cold colours),
the right panel shows voxels of GM (warm colours). The colour scale is
proportional to the density of the data in the plot. The median of the differences is shown as a
red dashed line; the two red dotted lines mark 95% limits of agreement.

Figure 5:
As in Figure 4 but showing the comparison between NODDI.a and NODDI.b.