0732
Towards unconstrained compartment modeling in white matter using diffusion-relaxation MRI with tensor-valued diffusion encoding1Clinical Sciences Lund, Medical Radiation Physics, Lund University, Lund, Sweden, 2Clinical Sciences Lund, Diagnostic Radiology, Lund University, Lund, Sweden, 3Brigham and Women's Hospital, Harvard Medical School, Boston, MA, United States, 4Clinical Sciences Lund, Department of Logopedics, Phoniatrics and Audiology, Lund University, Lund, Sweden, 5Clinical Sciences Malmö, Clinical Memory Research Unit, Lund University, Lund, Sweden
Synopsis
Microstructure imaging aims to estimate specific quantities such as the axonal density through modeling of diffusion MRI (dMRI) data. However, the low information content of conventional dMRI necessitates assumptions limiting the estimates’ accuracy. Here, we show how to replace model assumptions with independent information from tensor-valued diffusion encoding and diffusion-relaxation experiments. We present sampling protocols optimized using Cramér-Rao lower bounds allowing precise whole-brain estimation of compartment-specific fractions, diffusivities and T2 values in 15 minutes and show results from subjects of different ages. The approach greatly expands the set of parameters measurable with dMRI and provides parameter relations informing model constraints.
Introduction
Methods such as DTI and DKI provide sensitivity to the brain microstructure but do not report on specific quantities.1 Recent approaches aim to address this limitation by using models that parameterize the signal in terms of quantities such as the axonal density, which can then be estimated by fitting the model to acquired data.2 dMRI data normally support the estimation of just a few parameters,3 however, which necessitates model assumptions that limit the specificity of the estimates to a narrow range of conditions.4 Specificity across a wider range of conditions requires these model assumptions to be replaced with independent information obtained, for example, using additional acquisition dimensions such as the shape of the b-tensor in tensor-valued diffusion encoding5 or the echo time in diffusion-relaxation experiments.6 This study investigates how to combine the dimensions of b-value (b), b-tensor shape (bΔ) and echo time (TE) for maximal information encoding with respect to Cramér-Rao lower bounds (CRLB). We present clinically feasible sampling protocols allowing precise estimation of all parameters within a minimally constrained two-compartment diffusion-relaxation model and show results from children, adults, and elderly with white matter lesions.Methods
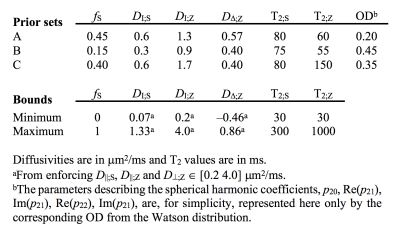
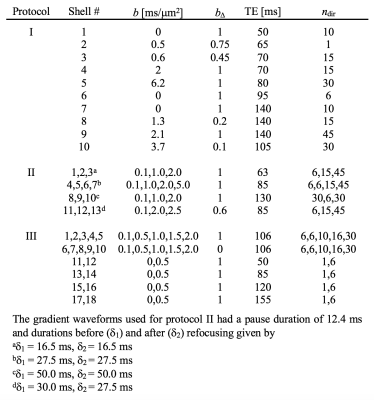
We used a two-compartment ‘stick’ (S) and ‘zeppelin’ (Z) diffusion-relaxation model for white matter featuring six free ‘kernel’ parameters and an orientation distribution function (ODF) described by a five-parameter truncated spherical harmonic series (Table 1). We described sampling protocols as sets of ‘shells’ defined by a b/bΔ/TE-combination and a number of directions (ndir). To compare protocols, we defined a ‘weighted parameter variance’ that averaged the CRLB of the kernel parameters across priors representing different types of tissue (Table 1). Protocols were optimized using the stochastic Self Organizing Migrating Algorithm (SOMA)7. A manually adapted protocol (Table 2; II) was used to acquire data with multiple bΔ and TE in five adults and five children on a MAGNETOM Prisma 3T system (Siemens Healthcare, Erlangen, Germany) using a prototype diffusion-weighted spin-echo sequence.8 The acquisition time was 15 minutes for whole-brain imaging using 2.5 mm3 voxels, TR = 3.4 s, GRAPPA factor 2 and multiband factor 2.9 Data were also acquired from five elderly subjects with white matter lesions using protocol III in Table 2. Model fitting was performed twice using least-squares minimization with random initial guesses and the parameter bounds in Table 1.Results
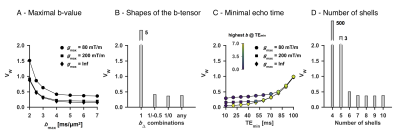
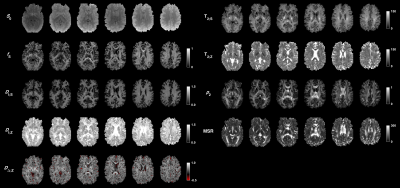
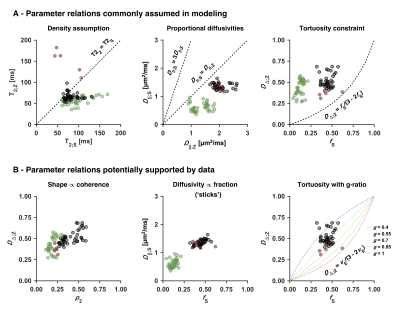
An optimized protocol is shown in Table 2 (I) together with the manually adapted protocol (II). Protocol optimization revealed a dramatic gain in precision from acquiring data using multiple bΔ and at least six shells (Fig. 1B and D). Precision was also improved from using higher maximal b-values (bmax; Fig. 1A) and lower TE (TEmin; Fig. 1C). Simulations showed that protocols with these properties resulted in precise parameter estimates and a single family of solutions even under full orientation dispersion (no branching was observed). In vivo parameter maps were smooth with a plausible contrast (Fig. 2). Compared with adults, children featured slightly lower ‘stick’ fractions in white matter and white matter lesions exhibited elevated isotropic diffusivities and T2 values for ‘zeppelins’. Notably, our estimates did not follow parameter relations previously assumed in modeling (Fig. 3A), including the ‘density assumption’ of equal compartment T2 values, ‘proportional diffusivities’ assumptions linking compartment axial diffusivities by a constant, and the ‘tortuosity constraint’ relating the ‘zeppelin’ shape to the ‘stick’ fraction. Other relations were potentially supported (Fig. 3B), including positive relations within white matter between the ‘zeppelin’ shape and the orientation coherence and between the ‘stick’ axial diffusivity and the ‘stick’ fraction, and the tortuosity constraint with variable g-ratios (not accounting for myelin assumes g = 1).Discussion
This work shows the requirements for efficient estimation of all parameters of a minimally constrained two-compartment diffusion-relaxation model (Table 1). Six unique b/bΔ/TE-combinations (shells) were required (Fig. 1D), which allow estimation of all six kernel parameters. Multiple shapes of the b-tensor were required (Fig. 1B), which resolves the degeneracy of the comparatively simpler ‘standard model’.10,11 Also, multiple echo times for high b-values were required (not shown), which distinguishes the T2 values of compartments with different anisotropy but similar isotropic diffusivities.4,6 In vivo, the low ‘stick’ fractions in gray matter agree with previous results indicating that axons and not dendrites drive diffusion anisotropy in the brain.4,12,13 The lower ‘stick’ fractions in white matter of children may reflect incomplete maturation,14 and the increased ‘zeppelin’ isotropic diffusivities and T2 values of white matter lesions are consistent with demyelination enlarging the extracellular space.15Conclusion
Optimized diffusion-relaxation sampling enabled precise and efficient whole-brain estimation of compartment-specific fractions, diffusivities and T2 values in 15 minutes. Acquiring data using the independent dimensions of b-value, b-tensor shape and echo time thus supported the estimation of six rotation-invariant parameters compared with two using conventional multishell dMRI.3 Our relatively unconstrained estimates disagreed with several commonly assumed parameter relations but suggested some others, indicating that the proposed approach may inform the constraints of microstructure models.Acknowledgements
We thank Siemens Healthcare for providing access to the pulse sequence programming environment, Thomas Witzel and Daniel Park for supporting the implementation of SMS into the FWF pulse sequence, and Massachusetts General Hospital for providing the SMS source code. The study was supported by grants from the Swedish Research Council (2016-03443) and the NIH (P41EB015902 and R01MH074794).References
1. Novikov D, Kiselev V and Jespersen S. On modeling. Magn. Reson. Med. 2018;79:3172-3193.
2. Alexander D, Dyrby T, Nilsson M, et al. Imaging brain microstructure with diffusion MRI: Practicality and applications. NMR Biomed. 2017;e3841.
3. Kiselev V and Il'yasov K. Is the “biexponential diffusion” biexponential? Magn. Reson. Med. 2007;57:464-469.
4. Lampinen B, Szczepankiewicz F, Novén M, et al. Searching for the neurite density with diffusion MRI: Challenges for biophysical modeling. Hum. Brain Mapp. 2019;40:2529-2545.
5. Westin C-F, Knutsson H, Pasternak O, et al. Q-space trajectory imaging for multidimensional diffusion MRI of the human brain. Neuroimage 2016;135:345-362
6. Veraart J, Novikov D and Fieremans E. TE dependent Diffusion Imaging (TEdDI) distinguishes between compartmental T2 relaxation times. Neuroimage 2018;182:360-369
7. Zelinka I. New optimization techniques in engineering. Springer 2004:167-217.
8. Szczepankiewicz F, Sjölund J, Ståhlberg F, et al. Tensor-valued diffusion encoding for diffusional variance decomposition (DIVIDE): Technical feasibility in clinical MRI systems. PLoS One 2019;14:e0214238
9. Setsompop K, Gagoski B, Polimeni J, et al. Blipped‐controlled aliasing in parallel imaging for simultaneous multislice echo planar imaging with reduced g‐factor penalty. Mag Reson Med. 2012;67:1210-1224.
10. Coelho S, Pozo J, Jespersen S, et al. Resolving degeneracy in diffusion MRI biophysical model parameter estimation using double diffusion encoding. Mag Reson Med. 2019;82:395-410.
11. Reisert M, Kiselev V and Dhital B. A unique analytical solution of the white matter standard model using linear and planar encodings. Mag Reson Med. 2019;81:3819-3825.
12. Jespersen S, Bjarkam C, Nyengaard J, et al. Neurite density from magnetic resonance diffusion measurements at ultrahigh field: comparison with light microscopy and electron microscopy. Neuroimage 2010;49:205-216.
13. Novikov D, Veraart J, Jelescu I, et al. Rotationally-invariant mapping of scalar and orientational metrics of neuronal microstructure with diffusion MRI. Neuroimage 2018;174:518-538.
14. Paus T, Zidjenbos A, Worsley K, et al. Structural maturation of neural pathways in children and adolescents: in vivo study. Science 1999;283:1908-1911.
15. Englund E and Brun A. White matter changes in dementia of Alzheimer's type: the difference in vulnerability between cell compartments. Histopathology 1990;16:433-439.
Figures