Introduction

Increased specificity to microstructural changes is the major motivation for developing biophysical models in diffusion MRI (dMRI). For white matter (WM), the Standard Model (SM)¹ has been widely adopted. For single pulsed-field gradient dMRI acquisitions, the inverse problem of estimating SM parameters is ill-posed without lengthy acquisitions and extremely high diffusion gradients^2,3,4. It has recently been proposed that complementary information from multidimensional dMRI⁵ resolves this degeneracy^6,7. Although several types of multidimensional dMRI acquisitions may be suitable, some will be more efficient and provide more accurate parameter estimates in noisy scenarios.
Here we propose a framework for optimal experiment design of multidimensional dMRI and apply it to the SM. The continuous high-dimensional acquisition space of all possible combinations of b-tensor encodings is explored. The optimal acquisition is a nontrivial combination of linear and planar tensor encoding (LTE, PTE), which is corroborated with simulations and in vivo experiments.

Theory

Multidimensional dMRI measurements are represented by a rank-2 symmetric b-tensor $$$\boldsymbol{B}$$$ (Fig.1 shows examples). Tensor eigenvalues define the shape and diffusion weighting (i.e. size), and the eigenvectors define the orientation.

The Standard Model signal is the convolution over the unit sphere
$$S(\boldsymbol{B})=S_0\int_{\mathbb{S}^2}\mathcal{P}(\hat{\mathbf{u}})\mathcal{K}(\boldsymbol{B},\hat{\mathbf{u}})\,dS_{\hat{\mathbf{u}}},$$
where $$$S_0\equiv{}S(\boldsymbol{B})|_{\boldsymbol{B}=0}$$$ is the non-weighted diffusion signal, $$$\mathcal{P}(\hat{\mathbf{u}})$$$ the fibres' orientation distribution function (ODF), and
$$\mathcal{K}(\boldsymbol{B},\hat{\mathbf{u}})=f\exp\bigl[-D_{\text{a}}B_{ij}u_iu_j\bigr]+(1-f)\exp\bigl[-bD_\text{e}^\perp-(D_\text{e}^\parallel-D_\text{e}^\perp)B_{ij}u_iu_j\bigr]$$
is the response signal (kernel) from a fibre segment oriented along $$$\hat{\mathbf{u}}$$$, acquired with the b-tensor $$$\boldsymbol{B}$$$ (Einstein's summation notation assumed). $$$f$$$ is the $$$T_2$$$-weighted intra-axonal signal fraction, and $$$D_{\text{a}}$$$, $$$D_\text{e}^\parallel$$$, and $$$D_\text{e}^\perp$$$ the axial intra-axonal, axial extra-axonal and radial extra-axonal diffusivities, respectively.

Cramér-Rao bounds (CRBs) are of widespread use for experiment design in estimation theory⁸. If some mild regularity conditions are satisfied, CRBs provide a theoretical lower limit to the variance of an unbiased estimator of the model parameters $$$\boldsymbol{\theta}=(\theta_1,\ldots,\theta_N)$$$⁸:
$$\boldsymbol{\Sigma}_{\boldsymbol{\theta}}\geq\operatorname{CRB}^{\boldsymbol{\theta}}=[I(\boldsymbol{\theta})]^{-1},\quad{}I_{ij}(\boldsymbol{\theta})=-\mathrm{E}\left[\frac{\partial^{2}}{\partial\theta_{i}\partial\theta_{j}}\log{}f(x\,|\,\boldsymbol{\theta})\right],\quad{}i,j=1,\ldots,N,$$
where $$$f(x\,|\,\boldsymbol{\theta})$$$ is the likelihood and $$$I(\boldsymbol{\theta})$$$ the Fisher information.

Methods

We search for the b-tensor set (B-set) maximising the precision in the kernel parameters ($$$\boldsymbol{\psi}=\{f,D_{\text{a}},D_\text{e}^\parallel,D_\text{e}^\perp\}$$$). Thus, our problem separates into the definition of a metric and its optimisation.

Metric definition. To simultaneously avoid discrete degeneracy^3,4 and maximise precision, we propose a two-step CRB-based metric. First, we compute $$$\operatorname{CRB}^{\boldsymbol{\theta}}$$$, the CRBs for $$$\boldsymbol{\theta}=\{D_{ij},C_{ijk\ell}\}$$$, the tensors from the second-order cumulant expansion of the signal:
$$\log(S)=\log(S_0)-B_{ij}D_{ij}+\tfrac12B_{ij}B_{k\ell}C_{ijk\ell}+{\cal O}(\boldsymbol{B}^3).$$
SM parameters are uniquely determined by $$$\boldsymbol{\theta}$$$ for non-isotropic ODF^6,7. Thus, maximising precision on $$$\boldsymbol{\theta}$$$ guarantees non-degenerate kernel estimation. Secondly, we consider the kernel as a function of the cumulants, $$$\boldsymbol{\psi}(\boldsymbol{\theta})$$$, and propagate $$$\operatorname{CRB}^{\boldsymbol{\theta}}\mapsto\operatorname{CRB}^{\boldsymbol{\psi}(\boldsymbol{\theta})}$$$, using the mapping from⁹:
$$\boldsymbol{\Sigma}_{\boldsymbol{\psi}}\geq\operatorname{CRB}^{\boldsymbol{\psi}}\simeq\frac{\partial\boldsymbol{\psi}(\boldsymbol{\theta})}{\partial\boldsymbol{\theta}}\operatorname{CRB}^{\boldsymbol{\theta}}\frac{\partial\boldsymbol{\psi}(\boldsymbol{\theta})}{\partial\boldsymbol{\theta}}^{t}.$$
Kernel bounds, $$$\operatorname{CRB}^{\boldsymbol{\psi}}$$$, are combined into a scalar and integrated over the (ground truth) kernel and ODF parameter space $$$\cal{H}$$$:
$$F\left(\boldsymbol{\psi},\left\{p_{\ell{}m}\right\}\right)=\sum_{a=1}^{4}\mathrm{CRB}_{aa}^{\boldsymbol{\psi}}/\boldsymbol{\psi}_{a}^{2},\qquad\hat{F}=\frac{1}{\operatorname{vol}(\mathcal{H})}\int_{\mathcal{H}}F\left(\boldsymbol{\psi},\left\{p_{\ell{}m}\right\}\right)d\boldsymbol{\psi}d\boldsymbol{\rho},$$
where $$$\boldsymbol{\rho}=\{p_{\ell{}m}\}$$$ are the ODF spherical harmonics coefficients. To speed up the computation, we average $$$F$$$ over 30 different ODF that correspond to isotropically oriented perpendicular fibre bundles and a single set of kernel parameters ($$$f=0.55,\,D_\text{a}=2.1\mu{}m^2/ms,\,D_\text{e}^{\parallel}=1.8\mu{}m^2/ms,\,D_\text{e}^\perp=0.7\mu{}m^2/ms$$$).

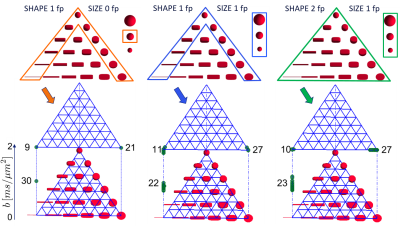
Optimisation. B-tensor eigenvectors were fixed and uniformly distributed over the hemisphere¹⁰. The optimisation selected the optimal combination of b-tensor eigenvalues that minimised our metric. We applied three sets of constraints (see Fig.2) progressively increasing the search volume, always limiting maximum b-value to $$$b_{\text{max}}=2ms/\mu{}m^2$$$. B-sets of $$$K\!=\!60$$$ b-tensors were considered. To avoid local minima, stochastic optimisation was used¹¹.

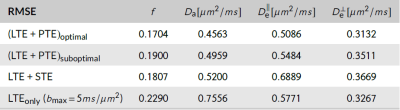
Noise propagation experiments were performed. The optimal protocol was compared against balanced combinations of LTE, PTE and spherical tensor encoding (STE) data (see Imaging). We generated synthetic signals from 7000 random voxels, added noise (SNR=100), estimated the kernel parameters and computed the root mean squared error (RMSE).

Imaging. Three normal volunteers (male-37y/o, male-33y/o, female-32y/o) were imaged on a Siemens Prisma system using a 64-channel head coil. Maxwell-compensated asymmetric waveforms¹² were used to generate four protocols, each consisting of a set of b-tensors oriented along 80 isotropically distributed directions and 6 $$$b=0$$$ images. The $$$(\text{LTE+PTE})_\text{optimal}$$$-protocol had $$$30\,\text{LTE}$$$ measurements at $$$b=1ms/\mu{}m^2$$$ and $$$16\,\text{LTE}+34\,\text{PTE}$$$ at $$$b=2ms/\mu{}m^2$$$. The $$$(\text{LTE+PTE})_\text{suboptimal}$$$-protocol had $$$10\,\text{LTE}+10\,\text{PTE}$$$ at $$$b=1ms/\mu{}m^2$$$ and $$$30\,\text{LTE}+30\,\text{PTE}$$$ at $$$b=2ms/\mu{}m^2$$$. The $$$\text{LTE+STE}$$$-protocol had $$$15\,\text{LTE}$$$ at $$$b=1ms/\mu{}m^2$$$, $$$41\,\text{LTE}$$$ at $$$b=2ms/\mu{}m^2$$$ and $$$6\,\text{STE}$$$ at $$$b=0.5,1,1.5,2ms/\mu{}m^2$$$. The $$$\text{LTE}_\text{only}$$$-protocol had $$$20\,\text{LTE}$$$ at $$$b=1ms/\mu{}m^2$$$ and $$$60\,\text{LTE}$$$ at $$$b=2ms/\mu{}m^2$$$. Imaging parameters: TR/E : $$$7200/94ms$$$, resolution: $$$2.5mm$$$ isotropic, in-plane FOV: $$$220mm$$$, GRAPPA acceleration factor $$$2$$$, no partial Fourier. Data was processed using DESIGNER¹³.

Results

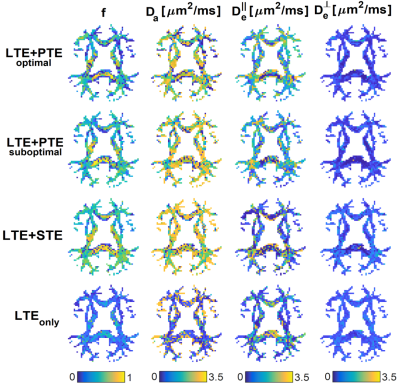
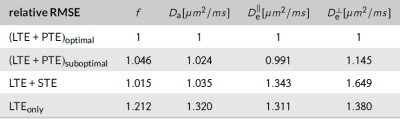
Optimal B-sets converge to two shells of LTE and PTE (see Fig.2). Simulations confirmed that the optimal acquisition has smaller errors than non-informed combinations of LTE+PTE, LTE+STE, or high-b LTE$$$_{\text{only}}$$$ data (see Fig.3 for RMSE values).
Fig.4 shows WM parametric maps for one subject. To assess reproducibility, we combined the independent measurements in these acquisitions and estimated SM parameters from the extended dataset. These estimates were used as ground truth and the estimation error was computed for each individual B-set. Averaged across the WM of all subjects, the RMSE was reduced in the optimised LTE+PTE combination (see Fig.5).

Discussion and Conclusion

We for the first time apply a CRB-based optimal experiment design framework to the SM. Our experiments show that a non-trivial combination of LTE and PTE data is optimal with two diffusion weightings.
Interestingly, no spherical or non-axially symmetric b-tensors are preferred. Hence, out of all the 2-dimensional b-tensor shape manifold of Fig.1, only 2 discrete shapes are relevant for optimal WM parameter estimation. This may have practical implications for optimised sequence design. Future work will explore high-b and varying TE.

Acknowledgements

This work has been supported by the OCEAN project (EP/M006328/1) and MedIAN Network (EP/N026993/1) both funded by the Engineering and Physical Sciences Research Council (EPSRC) and the European Commission FP7 Project VPH-DARE@IT (FP7-ICT-2011-9-601055). AFF acknowledges support from the Royal Academy of Engineering Chair in Emerging Technologies Scheme (CiET1819\19). SJ acknowledges financial support for a sabbatical at NYU from Aarhus University Research Foundation (AUFF), the Lundbeck Foundation (R291-2017-4375), and Augustinus Fonden (18-1456). SJ is also supported by the Danish National Research Foundation (CFIN), and the Danish Ministry of Science, Innovation, and Education (MINDLab). DSN and EF acknowledge support from NIH under NINDS award R01 NS088040.