0730

Estimating intra-axonal axial diffusivity with diffusion MRI in the presence of fibre orientation dispersion

Amy FD Howard¹, Alexandre A Khrapitchev², Jeroen Mollink^1,3, Rogier B Mars^1,4, Nicola Sibson², Jerome Sallet⁵, Saad Jbabdi¹, and Karla L Miller¹
¹FMRIB Centre, Wellcome Centre for Integrative Neuroimaging, Nuffield Department of Clinical Neurosciences, University of Oxford, Oxford, United Kingdom, ²CR-UK/MRC Oxford Institute for Radiation Oncology, Department of Oncology, University of Oxford, Oxford, United Kingdom, ³Department of Anatomy, Donders Institute for Brain, Cognition and Behaviour, Radboud University Medical Center, Nijmegen, Netherlands, ⁴Donders Institute for Brain, Cognition and Behaviour, Radboud University Nijmegen, Nijmegen, Netherlands, ⁵Wellcome Centre for Integrative Neuroimaging, Experimental Psychology, Medical Sciences Division, University of Oxford, Oxford, United Kingdom

Synopsis

Intra-axonal axial diffusivity could be interesting biomarker of disease, yet it is often assumed constant across the white matter. Furthermore, when intra-axonal diffusivity is estimated, few models account for fibre orientation dispersion which (when not explicitly modelled) will greatly affect the estimates of axial diffusion. Here we combine the stick model of intra-axonal diffusion with a simple model of fibre dispersion to simultaneously estimate intra-axonal axial diffusivity and fibre dispersion on a voxel-wise basis in high b-value data. Our results demonstrate considerable variability in the intra-axonal axial diffusivity across the white matter.

Introduction

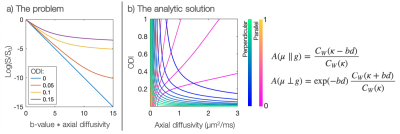
Diffusion MRI is a powerful tool for measuring microstructural features of the tissue (e.g. axon integrity, diameter and orientation). However, there is often interplay between the tissue architecture and the diffusion characteristics making signal interpretation challenging^1,2.

For example, intra-axonal axial diffusivity could be an important biomarker of disease but fibre orientation dispersion must be taken into account in order to estimate it properly. With even a small amount of fibre dispersion within an imaging voxel, the intra-axonal axial diffusivity appears to vary with b-value (Figure 1a). If dispersion is ignored, this apparent deviation from Gaussian diffusion (a.k.a. non-zero kurtosis) could be erroneously assigned to a complex diffusion micro-environment (a microstructure properties viewpoint), or it could bias the estimation of the axial diffusivity (a diffusion properties viewpoint). Popular current models presume a global axial diffusivity which is often either pre-defined³or estimated from the data⁴. If the assumed diffusivities are inaccurate, the estimation of the remaining model parameters will be biased.

Here we show that orientation dispersion and intra-axonal axial diffusivity can be estimated jointly in single-fibre voxels. The model is based on high b-value data where we assume that the diffusion signal can be exclusively assigned to intra-axonal water^1,5 with only axial diffusivity^1,5,6. We demonstrate in simulated data the effect of getting some of the model assumptions wrong. When applied to real data, the model shows substantial variability in both orientation dispersion and axial diffusivity across the brain.

Methods

The dispersed stick model
The diffusion attenuation

$A$ along gradient direction

$g$ is given by:

$A=\int_{S^2}\exp[\,\kappa(\mu^Tx)^2\,]\,\cdot\,\exp[\,-bd(g^Tx)^2\,]\,\text{d}x\,.\qquad\qquad\text{Eq.}\,1$

$d$ is the intra-axonal axial diffusivity;

$x$ , a unit vector on the sphere. Here the fibre orientation distribution is described by a Watson distribution^3,7 with orientation

$\mu$ , dispersion

$\kappa$ and normalising constant

$C_W$ , where,

$C_W(\kappa)=\sqrt{\frac{4\pi^3}{\kappa}}\,\text{erfi}(\sqrt{\kappa}))\,.\qquad\qquad\text{Eq.}\,2$
The orientation dispersion index is defined as

$ODI=2/\pi\,\text{arctan}(\kappa)$ ³.

The model is based on four main assumptions:

The fibre orientation distribution is accurately described by a Watson distribution with a known fibre orientation.
Water experiences axons to be like “sticks” with no measurable radial diffusion.
There is a negligible contribution from extra-cellular water.
The voxel contains a single dispersed fibre population.

The latter is enforced because the volume fractions and axial diffusivities of crossing fibre populations are degenerate.

The integral in Equation 1 has an analytic form, two examples of which are shown in Figure 1b. We see how the combined analysis of

$\geq2$ gradient directions (which aren’t both perpendicular to the fibre) provides a unique solution for both the within-voxel fibre dispersion and axial diffusivity.

Simulations
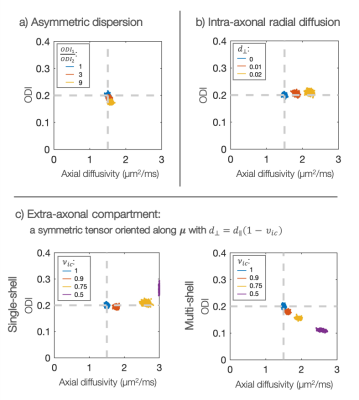
Simulated data (noiseless, 32 gradient directions) was used to examine the effect of deviations from the assumptions 1-3 in turn.

Data
The model was fitted to diffusion MRI data acquired at

$7\,\text{T}$ (Agilent,

$400\,\text{mT/m}$ ) in a perfusion-fixed, postmortem macaque brain⁸:

$b=7,10\,\text{ms/µm}^2$ ,

$1000$ gradient directions,

$1\,\text{mm}$ isotropic voxels. The diffusion tensor⁹ was fitted to the data and single-fibre voxels selected with

$FA>0.5$ , linearity

$(L_1-L_2)\,/\,L_1\geq0.4$ , planarity

$(L_2-L_3)\,/\,L_1\leq0.2$ and sphericity

$L_3/L_1\leq0.35$ ^10,11. The fibre orientation was assumed equal to

$V_1$ .

In both simulated and real data, the model was optimised using a Markov chain Monte Carlo (MCMC) method¹².

Results and discussion

Simulations
Figure 2 considers sensitivity to modelling assumptions. If the intra-axonal stick model holds true, the axial diffusivity can be measured with good precision and accuracy in the case of asymmetric dispersion (Figure 2a). Violation of the stick-model increases the estimated diffusivity (Figure 2b). Figure 2c highlights the importance of working at high b-values where the extra-axonal signal is negligible^1,5. Interestingly, the effect of extra-axonal water was different in single- or multi-shell analysis.

Data
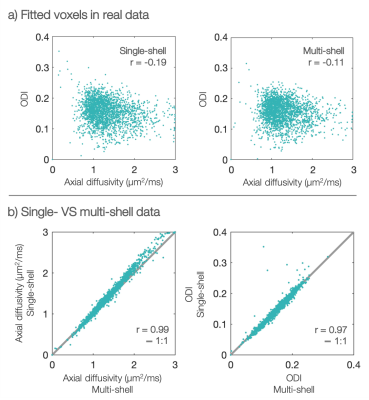
In the postmortem macaque brain, the estimates of axial diffusivity and fibre dispersion appear fairly uncorrelated (Figure 3a). The results from single-shell data closely match those from multi-shell data (Figure 3b), though with a slight bias in axial diffusivity. This is likely due to either non-Gaussian diffusion, extra-axonal contributions or non-stick-like fibres.

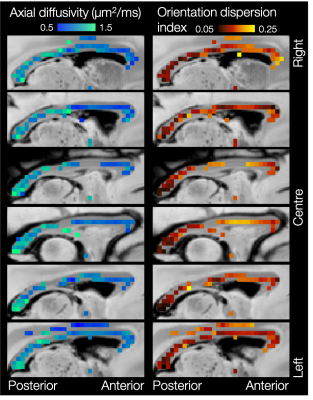
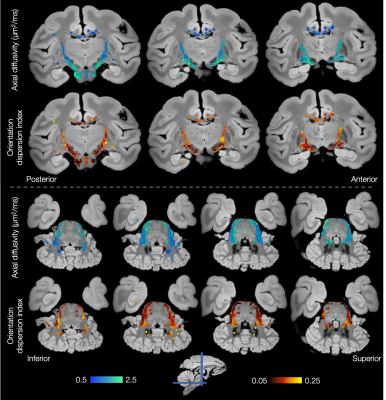
Figures 4 and 5 show considerable variation in axial diffusivity and fibre dispersion across the white matter. The corpus callosum shows low axial diffusivity in the genu and high in the splenium, as well as a low-high-low pattern of dispersion, particularly towards the midline. These results are consistent with previous observations of both dispersion^13,14,15,16 and axon diameter^15,17,18,19.

Both the inferior cortico-spinal tract and transverse pontocerebellar fibres (Figure 5) show notably high axial diffusivities and low dispersion. Generally lower values of axial diffusivity and higher dispersion are seen in the middle cerebellar peduncles and cerebellar white matter.

Finally, Figures 4 and 5 demonstrate left-right symmetry and spatial smoothness, matching symmetric and smoothly changing anatomy.

Conclusion

Through the simultaneous analysis of orientation dispersion and axial diffusivity we demonstrate substantial variability in the intra-axonal axial diffusivity within single-fibre voxels across the brain. These results question the assumption of a global axial diffusivity^3,4. Furthermore, this variability suggests that axial diffusivity could act as an interesting biomarker of disease. Here we analyse perfusion-fixed postmortem tissue which likely explains the low values of diffusivity reported here when compared to those in vivo^11,20,21. These ex vivo data will provide the opportunity to compare dispersion estimates to microscopy-derived equivalents in the same brain^8,14. Future works will apply the model to in vivo human data.

Acknowledgements

This work was supported by the Wellcome Trust (grant WT202788/Z/16/A), EPSRC and MRC (grants EP/L016052/1 and MR/L009013/1). AK and NS were funded by Cancer Research UK (grant C5255/A15935). The work of RBM is supported by the Biotechnology and Biological Sciences Research Council (BBSRC) UK [BB/N019814/1]. JS was supported by a Sir Henry Dale Wellcome Trust Fellowship (105651/Z/14/Z). The Wellcome Centre for Integrative Neuroimaging is supported by core funding from the Wellcome Trust (203139/Z/16/Z). It should be noted that SJ and KM contributed equally to this work.

References

1. Novikov DS, Veraart J, Jelescu IO, Fieremans E, Rotationally-invariant mapping of scalar and orientational metrics of neuronal microstructure with diffusion MRI, NeuroImage, 174, 7, 2018.

2. Coelho S, Pozo JM et al., Resolving degeneracy in diffusion MRI biophysical model parameter estimation using double diffusion encoding, Magnetic Resonance in Medicine, 82, 1, 7, 2019.

3. Zhang H, Schneider T, Wheeler-Kingshott CA, Alexander DC, NODDI: Practical in vivo neurite orientation dispersion and density imaging of the human brain, NeuroImage, 61, 4, 7, 2012.

4. Tournier JD, Yeh CH et al., Resolving crossing fibres using constrained spherical deconvolution: Validation using diffusion-weighted imaging phantom data, NeuroImage, 42, 2, 8, 2008.

5. Veraart J, Fieremans E, Novikov D, On the scaling behavior of water diffusion in human brain white matter, NeuroImage, 185, 1, 2019.

6. Kroenke CD, Ackerman JJ, Yablonskiy DA, On the nature of the NAA diffusion attenuated MR signal in the central nervous system, Magnetic Resonance in Medicine, 52, 5, 2004.

7. Mardia KV, Jupp PE, Directional Statistics, Wiley & Sons, 2000.

8. Howard AFD, Jbabdi S et al., The BigMac dataset: ultra-high angular resolution diffusion imaging and multi-contrast microscopy of a whole macaque brain, ISMRM 27th Annual Meeting, 2019.

9. Basser PJ, Mattiello J, Le Bihan D, MR diffusion tensor spectroscopy and imaging, Biophysical Journal, 66, 1, 1994.

10. Fieremans E, Jensen JH, Helpern JA, White matter characterization with diffusional kurtosis imaging, Neuroimage, 58, 2011.

11. Dhital B, Reisert M, Kellner E, Kiselev VG, Intra-axonal diffusivity in brain white matter, NeuroImage, 189, 4, 2019.

12. Hastings WK, Monte Carlo sampling methods using Markov chains and their applications, Biometrika, 57, 1, 1970.

13. Budde MD, Annese J, Quantifying anisotropy and fiber orientation in human brain histological sections, Frontiers in Integrative Neuroscience, 1, 2013.

14. Mollink J, Kleinnijenhuis M et al. Evaluating fibre orientation dispersion in white matter: Comparison of diffusion MRI, histology and polarized light imaging, NeuroImage, 157, 8, 2017.

15. Zhang H, Hubbard PL, Parker GJM, Alexander DC, Axon diameter mapping in the presence of orientation dispersion with diffusion MRI, NeuroImage, 56, 3, 6 2011.

16. Mollink J, Smith SM et al., The spatial correspondence and genetic influence of interhemispheric connectivity with white matter microstructure, Nature Neuroscience, 22, 5, 5, 2019.

17. Aboitiz F, Scheibel AB, Fisher RS, Zaidel E, Fiber composition of the human corpus callosum, Brain Research, 598, 1-2, 12, 1992.

18. Alexander DC, Hubbard PL et al., Orientationally invariant indices of axon diameter and density from diffusion MRI, NeuroImage, 52, 4, 10, 2010.

19. Barazany D, Basser PL, Assaf Y, In vivo measurement of axon diameter distribution in the corpus callosum of rat brain, Brain, 132, 5, 5, 2009.

20. Shepherd TM, Thelwall PE, Stanisz GJ, Blackband SJ, Aldehyde fixative solutions alter the water relaxation and diffusion properties of nervous tissue, Magnetic Resonance in Medicine, 62, 1, 2009.

21. Miller KL, Stagg CJ et al., Diffusion imaging of whole, post-mortem human brains on a clinical MRI scanner, Neuroimage, 57, 1, 2011.

Figures

a) In the presence of fibre orientation dispersion, the diffusion signal appears to vary with b-value. Thus, the orientation dispersion and axial diffusion should be estimated jointly. b) Equation 1 can be solved analytically for gradient directions

$g$ both perpendicular and parallel to the fibre

$\mu$ . When analysed separately, each gradient orientation produces a degenerate solution (each line shows combinations of

$ODI$ and axial diffusivity which produce the same diffusion signal), but when combined, provide a unique solution (where the lines intersect).

Violations of the model assumptions. Data was simulated for a) asymmetric fibre dispersion, b) non-stick like fibres (axially symmetric diffusion tensor), and c) an extra-axonal compartment. Here the radial diffusion

$d_\perp$ is linked to the intracellular volume fraction

$\nu_{ic}$ ³. In each case, the model was fitted assuming a Watson-like fibre distribution, stick-like diffusion and no extra-axonal contribution. Each point shows a single MCMC sample. Note that the multi-shell model assumes Gaussian intra-axonal axial diffusion.

Estimation of the intra-axonal axial diffusivity and orientation dispersion index in 2284 single-fibre voxels in a fixed, postmortem macaque brain. Each dot indicates a single voxel. a) Reassuringly, the estimated fibre dispersion and axial diffusivity appear fairly uncorrelated. b) Comparison of the results for single- (b = 10 ms/µm²) and multi-shell (b = 7,10 ms/µm²) data. We see a very close correspondence between the estimated

$ODI$ and a slight inflation of the single-shell axial diffusivities when compared to their multi-shell equivalents.

Variations in the intra-axonal axial diffusivity (left) and fibre orientation dispersion (right) across the corpus callosum for single-shell (b = 10 ms/µm²) data. For interpretation, the results are overlaid on a structural image. We see a consistent pattern of low axial diffusivities in the genu (anterior) and higher diffusivities in the splenium (posterior). In comparison, we see a low-high-low pattern of the orientation dispersion, particularly at the midline.

Variations in axial diffusivity and fibre orientation dispersion in the cortico-spinal tract (top) and pons (bottom) for b = 10 ms/µm² data. Note the change in scale bar from Figure 4: the axial diffusivity in more inferior brain regions was generally higher, with the highest values often found in the brain stem. Top: The inferior cortico-spinal tract shows particularly high axial diffusivities and low dispersion. Bottom: We see higher axial diffusion and lower dispersion in the anterior pons when compared to middle cerebellar peduncles and areas of the cerebellum.

Proc. Intl. Soc. Mag. Reson. Med. 28 (2020)

0730