0718

A unified framework for analysis of time-dependent diffusion: numerical validation of a restriction-exchange correlation experiment

Markus Nilsson¹, Carl-Fredrik Westin², Jan Brabec¹, Samo Lasic³, and Filip Szczepankiewicz¹
¹Clinical Sciences Lund, Lund University, Lund, Sweden, ²Brigham and Women's hospital, Harvard Medical School, Boston, MA, United States, ³Random Walk Imaging AB, Lund, Sweden

Synopsis

Probing time-dependence with diffusion MRI enables mapping of microstructure features such as cell sizes (restrictions) and membrane permeability (exchange). However, restrictions and exchange have opposite effects on the MR signal, and cannot be distinguished by just varying the diffusion time. We propose a unified framework for analysis of time-dependent diffusion that enables the design of efficient restriction-exchange correlation experiments. A signal representation was developed featuring parameters connected to restricted diffusion and exchange. This connection was validated by numerical simulations.

Introduction

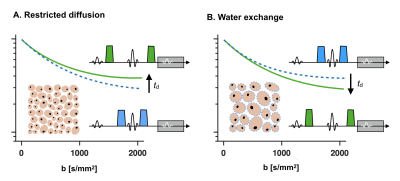
Probing time-dependence with diffusion MRI provides observables sensitive to cell sizes (restrictions) and membrane permeability (exchange).¹ Restrictions and exchange have opposite effects on the signal, however, and cannot be distinguished by varying the uni-dimensional diffusion-time parameter (Fig. 1). Here, we define a two-dimensional restriction-exchange parameter space and show how this space can be efficiently sampled by free gradient waveforms. While the restriction dimension is long known,^2,3 the exchange dimension was only recently derived.⁴ We also present a signal representation for data analysis that defines the appropriate model complexity for this type of acquisitions.

Theory

Diffusion encoding is performed by an effective gradient waveform g(t). We seek to describe the waveform in terms of interpretable encoding parameters, each connected to an independent aspect of the microstructure. Here, three parameters—previously defined, but not unified—was used. The first controls the diffusion weighting ($$$b$$$). The second controls the encoding of restricted diffusion, and is defined as the variance of the encoding spectrum ($$$V_\omega$$$).⁵The third controls the encoding of exchange ($$$\Gamma$$$).⁴ These are computed from g(t) by integral functions previously defined.^4,5

The three parameters are connected to observables sensitive to characteristic microstructure features via a signal representation. This was developed by first approximating the diffusion-weighting in a single compartment by $$$S~=~\exp(-A)$$$, where the attenuation factor is defined as $$A=b(D~+~V_\omega\,\cdot\,R),$$ where $$$D$$$ is the time-independent diffusivity. $$$R$$$ describes effects of restricted diffusion, and is defined as $$$R=c~\cdot~d^4/D_0$$$, where $$$c$$$ depends on the geometry of the compartment ($$$c=7/1536$$$ for cylinders).^5,6 Furthermore, $$$d$$$ is a characteristic size, and $$$D_0$$$ is the bulk diffusivity. Note that $$$D=0$$$ and $$$R>=0$$$ for restricted diffusion, whereas Gaussian diffusion gives $$$D>0$$$ and $$$R=0$$$. The expression was derived using a Taylor expansion of the diffusion spectrum and is valid for moderate b-values and compartment sizes below a threshold that depends on the encoding time.⁵
Signals from a mixture of compartments is approximated by a second-order cumulant expansion
$$S/S_0=\langle\exp(-A)\rangle\approx\exp(–b\,\cdot\,E~+~\tfrac{1}{2}b^2\,\cdot\,V),$$ where $$E=E_D~+~V_\omega\,\cdot\,E_R$$ and $$V=V_D~+~V_\omega\,\cdot\,C_{D,R}~+~V_\omega^2\,\cdot\,V_R.$$ The observables are the average diffusivity ($$$E_D$$$), average restriction coefficient ($$$E_R$$$), intra-voxel variance in diffusivities ($$$V_D$$$), correlation between diffusivities and restriction coefficients ($$$C_{D,R}$$$), and the variance in restriction coefficients ($$$V_R$$$). In the presence of exchange, $$S/S_0=\exp(–b\,\cdot\,E~+~\tfrac{1}{2}b^2\,\cdot\,V\,\cdot\,[1~–~\Gamma\,\cdot\,k]),$$ where $$$k$$$ is the final observable representing the average apparent exchange rate in the system.⁴ The expression is valid for systems with slow barrier-limited exchange.

Methods

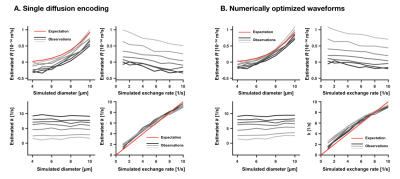
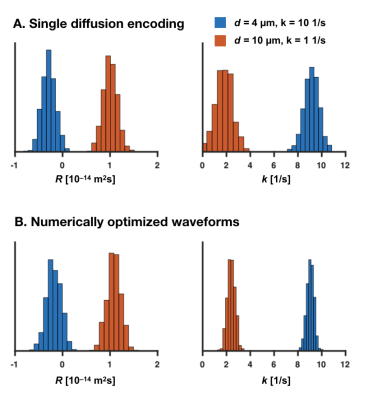
Gradient waveforms with a total duration of 100 ms were optimized to provide a variation in $$$V_\omega$$$, and $$$\Gamma$$$. In total, 9 waveforms were defined using single diffusion encoding (SDE), and 9 used non-pulsed waveforms. The target was to reach b = 2.5 ms/µm² at a system with a maximal gradient amplitude of 80 mT/m. For each waveform, the b-value was varied in 16 steps, resulting in 144 samples.
To assess whether the parameters in the signal representation can separate effects of restricted diffusion and exchange, Monte Carlo simulations were performed in a 2D-substrate with circular and uniformly arranged compartments,⁷ using a step length of 0.1 µm, a bulk diffusivity of 2.8 µm²/ms, and 10⁶ particles. Systems were simulated featuring diameters between 4 and 10 µm and exchange times between 100 and 1000 ms. The signal representation was fitted to signals generated from the Monte Carlo simulations. This was first performed without noise to estimate accuracy. Precision was estimated after adding noise with a generous SNR of 200. The analysis focused on two observables, $$$R$$$ and $$$k$$$, connected to restricted diffusion and exchange, respectively.

Results

Figure 2 visualizes waveforms optimized for maximal variation in $$$V_\omega$$$ and $$$\Gamma$$$, and shows that higher variability can be achieved by the optimized gradient waveforms even though the duration of the experiment is the same (Fig. 2). Figure 3 shows that $$$R$$$ was sensitive to variations in the simulated cylinder diameter, whereas $$$k$$$ was sensitive to variations in the simulated exchange rate. The crosstalk between the parameters was small, meaning that variations in the diameter had limited impact on $$$k$$$, and variation in the exchange rate had a limited impact on $$$R$$$. Figure 4 shows that the protocol featuring the wider range of values for $$$V_\omega$$$ and $$$\Gamma$$$ from optimized waveforms achieved more precise estimates compared with the protocol based on single diffusion encoding.

Discussion

We propose a unified framework for analysis of time-dependent diffusion that facilitates the design of efficient restriction-exchange correlation experiments. Compared to previous model-based approaches limited to pulsed gradients,^8,9 this approach leverages the power of free gradient waveforms and makes fewer assumptions. A signal representation was developed featuring parameters connected to restricted diffusion and exchange, tentatively validated by numerical simulations (Fig. 3). Previous representations featured the restriction and exchange dimensions separately,^5,10 but not together. Parameters could be estimated with high precision, although with some bias, as expected when using a truncated cumulant expansion.¹¹ The theory can be used to optimize imaging protocols and analyze the efficiency of experimental designs – if all waveforms are collinear in $$$V_\omega$$$ and $$$\Gamma$$$ we know that exchange and restricted diffusion cannot be separated. Future work will extend the analysis to include encoding tensors, and experimentally validate the theory and its interval of validity.

Acknowledgements

We acknowledge the following research grants Swedish Research Council (2016-03443), NIH P41EB015902, and NIH R01MH074794.

References

1. Nilsson, M., van Westen, D., Ståhlberg, F., Sundgren, P. C., & Lätt, J. (2013). The role of tissue microstructure and water exchange in biophysical modelling of diffusion in white matter. Magn Reson Mater Phy, 26(4), 345–370.

2. Stepisnik, J. (1993). Time-dependent self-diffusion by NMR spin-echo. Physica B, 183(4), 343–350.

3. Callaghan, P. (1997). A simple matrix formalism for spin echo analysis of restricted diffusion under generalized gradient waveforms. J Magn Reson, 129(1), 74–84.

4. Ning, L., Nilsson, M., Lasič, S., Westin, C.-F., & Rathi, Y. (2018). Cumulant expansions for measuring water exchange using diffusion MRI. J Chem Phys, 148(7), 074109–074112.

5. Nilsson, M., Lasič, S., Drobnjak, I., Topgaard, D., & Westin, C.-F. (2017). Resolution limit of cylinder diameter estimation by diffusion MRI: The impact of gradient waveform and orientation dispersion. NMR Biomed, 127(10), e3711–13.

6. Burcaw, L. M., Fieremans, E., & Novikov, D. S. (2015). Mesoscopic structure of neuronal tracts from time-dependent diffusion. NeuroImage, 114(C), 18–37.

7. Nilsson, M., Alerstam, E., Wirestam, R., Ståhlberg, F., Brockstedt, S., & Lätt, J. (2010). Evaluating the accuracy and precision of a two-compartment Kärger model using Monte Carlo simulations. J Magn Reson, 206(1), 59–67.

8. Stanisz, G. J., Szafer, A., Wright, G. A., & Henkelman, M. (1997). An Analytical Model of Restricted Diffusion in Bovine Optic Nerve. Magn Reson Med, 37, 103–111.

9. Nedjati-Gilani, G. L., Schneider, T., Hall, M. G., Cawley, N., Hill, I., Ciccarelli, O., et al. (2017). Machine learning based compartment models with permeability for white matter microstructure imaging. NeuroImage, 150, 119–135.

10. Lasič, S., Nilsson, M., Lätt, J., Ståhlberg, F., & Topgaard, D. (2011). Apparent exchange rate mapping with diffusion MRI. Magn Reson Med, 66(2), 356–365. http://doi.org/10.1002/mrm.22782

11. Chuhutin, A., Hansen, B., & Jespersen, S. N. (2017). Precision and accuracy of diffusion kurtosis estimation and the influence of b-value selection. NMR Biomed, 30(11).

Figures

Fig. 1. Restricted diffusion (A) and water exchange (B) have opposite effects on the diffusion weighted signal. As such, any attempt to measure one of the features will be confounded by the other, even if the diffusion encoding is designed to modulate the diffusion time ($$$t_D$$$). Resolving this situation requires a unified theory for both effects, and an experimental design that can disentangle the two effects.

Fig. 2. Top row shows plots of the two experimental parameters $$$V_\omega$$$, and $$$\Gamma$$$ for waveforms based on single diffusion encoding (A) and numerically optimized waveforms (B), respectively. Bottom row shows the waveforms, color coded to match corresponding points in the time-parameter landscape. Note that the parameter space is larger with free waveforms compared with the pulsed waveforms (gray shaded area).

Fig. 3. Plots show the accuracy of the estimated parameters. On-diagonal plots show estimated values in gray and expected values in red. Off-diagonal plots show the crosstalk between restricted diffusion and exchange. Exchange had an impact on the restricted diffusion parameter $$$R$$$, but diameter had limited impact on $$$k$$$. Both protocols generally yield high accuracy, with a slightly stronger negative bias in $$$R$$$ for the single diffusion encoding protocol.

Fig.4. Precision in parameter estimates. Histograms in blue and red show parameter estimates for two ground-truth cases with diameters of 4 and 10 µm and exchange times of 100 and 1000 ms, respectively. The numerically optimized waveforms featured the highest precision in the estimated exchange rates.

Proc. Intl. Soc. Mag. Reson. Med. 28 (2020)

0718