0686
Highly Accelerated MPRAGE Imaging of the Brain Incorporating Deep Learning Priors with Subject-Specific Novel Features
Yue Guan1, Yudu Li2,3, Ziyu Meng3,4, Tianyao Wang5, Rong Guo2,3, Ruihao Liu4, Yao Li4, Yiping Du4, and Zhi-Pei Liang2,3
1Institute for Medical Imaging Technology, School of Biomedical Engineering, Shanghai Jiao Tong University, Shanghai, China, 2Department of Electrical and Computer Engineering, University of Illinois at Urbana-Champaign, Urbana, IL, United States, 3Beckman Institute for Advanced Science and Technology, University of Illinois at Urbana-Champaign, Urbana, IL, United States, 4Shanghai Jiao Tong University, Shanghai, China, 5Department of Radiology, The Fifth People's Hospital of Shanghai, Shanghai, China
1Institute for Medical Imaging Technology, School of Biomedical Engineering, Shanghai Jiao Tong University, Shanghai, China, 2Department of Electrical and Computer Engineering, University of Illinois at Urbana-Champaign, Urbana, IL, United States, 3Beckman Institute for Advanced Science and Technology, University of Illinois at Urbana-Champaign, Urbana, IL, United States, 4Shanghai Jiao Tong University, Shanghai, China, 5Department of Radiology, The Fifth People's Hospital of Shanghai, Shanghai, China
Synopsis
MPRAGE imaging has been widely used in clinical applications and various attempts have been made for its acceleration. This paper presents a new method to accelerate MPRAGE imaging using sparse and random sampling of k-space and constrained reconstruction incorporating image priors and subject-specific novel features. In our current implementation, the MPRAGE image priors were obtained using deep learning on data from the Human Connectome Project, and novel localized features were recovered by solving a sparsity-constrained reconstruction. In vivo experimental results demonstrated that the proposed method can produce high-quality whole-brain MPRAGE images in 0.7x0.7x0.7 mm3 nominal resolution from a 1.5-min scan.
Introduction
MPRAGE scans have been widely used to provide high-quality T1-weighted images. However, 3D scans with a whole-brain coverage at submillimeter spatial resolution usually take more than 10 minutes without acceleration 1. There have been several attempts to accelerate MPRAGE imaging, including parallel imaging based techniques 1, compressive sensing (CS) based methods2 and the emerging machine learning-based methods 3. Existing methods have pretty much fully taken advantage of the acceleration capability offered by conventional parallel imaging and compressive sensing. Deep learning-based methods promise to provide additional accelerations 4. While machine learning-based methods can take advantages of the prior image information embedded in the training data, most of the existing methods usually require large amounts of training data to learn the image priors properly; otherwise significant image artifacts/errors can occur 5. This paper presents a new method to accelerate MPRAGE imaging by synergistically integrating parallel imaging, machine learning priors, and sparse modeling to achieve stable reconstructions from highly sparse k-space data. In our current implementation, the MPRAGE image priors were obtained using deep learning on the HCP data 6; novel localized features were recovered by solving a sparsity-constrained reconstruction. Experimental results demonstrated that the proposed method can produce high-quality whole-brain MPRAGE images in 0.7x0.7x0.7 mm3 nominal resolution from a 1.5-min scan.Methods
An overview of the proposed method is shown in Fig. 1.
Data Acquisition :
A dual-density sampling strategy was used to cover k-space (Fig. 1). More specifically, k-space was divided into two parts with central k-space being fully sampled and outer k-space being sparsely sampled in a random fashion along both phase encoding directions. With such a sampling scheme, the total data acquisition time for a whole-brain MPRAGE scan was about 1.5-min to achieve 0.7x0.7x0.7 mm3 nominal resolution.
DL-based image priors :
Existing DL-based image reconstruction methods take the sparsely sampled k-space data or the aliased images as the input and learn the highly complex nonlinear relationship between the sparse k-space data (or aliased images) and the desired images. This is a very high-dimensional mapping problem, which requires large amounts of training data to ensure stable solutions. We addressed this problem using the following strategy: a) utilizing the large MPRAGE brain image database from HCP for training, b) simplifying the mapping relationship by using the CS reconstruction from the sparse data as the input, and c) using the machine learning based reconstruction only as an initial estimate and recovering the differences using an additional compensating model.
To capture the MPRAGE image priors from the HCP data, we adopt the state-of-the-art architecture in SRGAN7, in which the generator network was replaced by a multi-scale residual U-net 8 due to its artifact removal capability enabled by the residual learning block.The loss function was defined as a combination of Mean Absolute Error (MAE) and WGAN-GP loss 9, which gave better convergence. To further improve training efficiency, we applied geometrical normalization to the original HCP data using diffeomorphic image registration to reduce the spatial variations among different subjects 10.
Recovery of subject-dependent novel features:
Most existing deep learning-based reconstruction methods accept the output of the trained neural network as the final solutions3, or use it as a prior to be included in a regularized image reconstruction method11. Recognizing that the machine learning priors are not accurate and also biased towards the training data collected from healthy volunteers, we incorporated in our reconstruction model an explicit term to represent subject-specific novel features (to capture any difference between the DL-based reconstruction and newly acquired data). To this end, we expressed the final reconstruction as $$$\rho_{DL}(x)+\rho_n(x)$$$, where $$$\rho_{DL}(x)$$$represents the initial reconstruction from the trained DL network and $$$\rho_n(x)$$$represents novel features. The novel features were recovered by solving the following constrained reconstruction:
$$\hat{\rho}_n=\arg\min_{\{c_n\},\rho_n}\Vert d-\Omega F S(\rho_{DL}(x)+\rho_n(x))\Vert^2_2+\lambda\Vert W \rho_n(x)\Vert_1$$
where $$$d$$$ denotes the measured data, S the sensitivity map estimated from the fully sampled central k-space data, F the sampling operator, $$$\Omega$$$ the sampling mask, W the sparsifying transform and $$$\lambda$$$ the regularization parameter.
In Vivo Imaging
In vivo experiments were performed to evaluate the performance of the proposed method. The data were collected from patients on a 3T scanner with TR/TE = 2400/2.41 ms, FOV = 224×224×157 mm3, matrix size = 320×320×224 according to the MPRAGE imaging protocol in HCP.
Results
Figure 2 shows the DL-based reconstructions obtained using CS reconstructions and Fourier reconstructions as the input, respectively. Figure 3 illustrates the capability of the proposed method to recover subject-dependent novel features. Figure 4 shows a set of representative MPRAGE images reconstructed from experimental data collected in 1.5 minutes using the proposed method.Conclusion
This paper presents a novel method to accelerate whole-brain MPRAGE imaging. The proposed method has three key features: a) accelerating data acquisition with sparse and random sampling of k-space, b) reducing learning complexity by using the CS reconstructions as the input, and c) using the machine learning output only as an initial estimate and recovering the subject-dependent novel features using a sparse model.In-vivo experimental results demonstrated that the proposed method can produce high-quality whole-brain MPRAGE images with 0.7x0.7x0.7 mm3nominal resolution and 1.5-min scan time. With further improvement, the method may prove useful for accelerating MPRAGE scans for clinical applications.Acknowledgements
References
- Polak D, Setsompop K, Cauley SF, et al. Wave‐CAIPI for highly accelerated MP‐RAGE imaging. Magn. Reson. Med. 2018;79(1):401-406.
- Lustig M, Donoho D, Pauly J. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn. Reson. Med. 2007;58(6):1182-1195.
- Yang G, Yu S, Dong H, et al. DAGAN: deep de-aliasing generative adversarial networks for fast compressed sensing MRI reconstruction. IEEE Trans. Med. Imaging. 2017;37(6):1310-1321.
- Mardani M, Gong E, Cheng J, et al. Deep generative adversarial neural networks for compressive sensing MRI. IEEE Trans. Med. Imaging. 2018;38(1):167-179.
- Antun V, Renna F, Poon C, et al. On instabilities of deep learning in image reconstruction-Does AI come at a cost? arXiv:1902.05300.
- Van Essen D, Smith S, Barch D, et al. The WU-Minn human connectome project: an overview. Neuroimage. 2013;80:62-79.
- Ledig C, Theis L, Huszár F, et al. Photo-realistic single image super-resolution using a generative adversarial network. 30th Proceedings of the IEEE conference on computer vision and pattern recognition. 2017;105-114.
- Lee D, Yoo J, Tak S, et al. Deep residual learning for accelerated MRI using magnitude and phase networks. IEEE Trans. Biomed. Eng. 2018;65(9):1985-1995.
- Gulrajani I, Ahmed F, Arjovsky M, et al. Improved training of wasserstein GANs. Advances in neural information processing systems. 2017;30:5767-5777.
- Ashburner J. A fast diffeomorphic image registration algorithm. Neuroimage. 2007;38(1):95-113.
- Wang S, Su Z, Ying L, et al. Accelerating magnetic resonance imaging via deep learning. 2016 IEEE 13th International Symposium on Biomedical Imaging (ISBI). 2016:514-517.
Figures
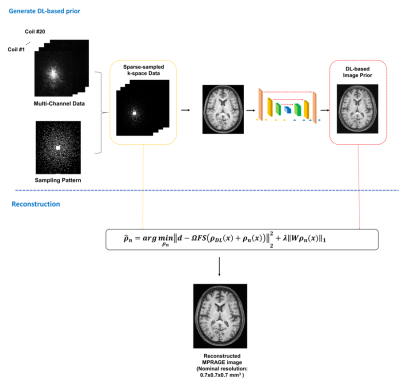
Figure 1: An overview of the proposed method.
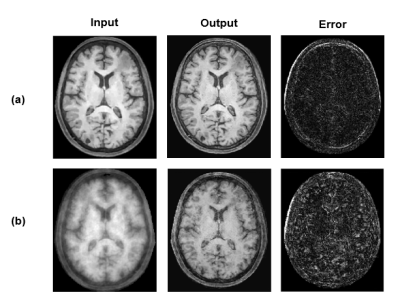
Figure 2: In vivo
results comparing the DL-generated image prior with: (a) compressed sensing reconstructions and (b)
zero-filled reconstructed images, as input.
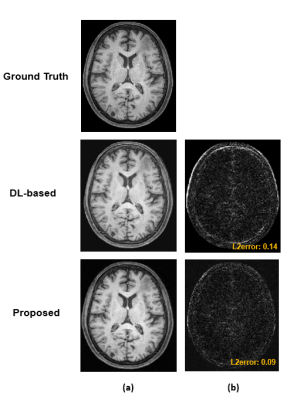
Figure
3: Comparison of DL-based reconstructions and those from the proposed method.
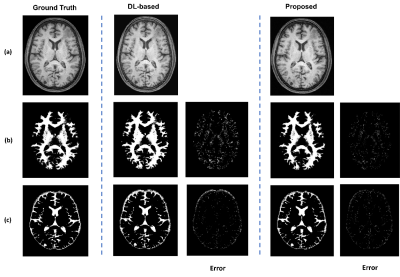
Figure 4:
Demonstration of the high-resolution imaging capability of the proposed method.
The MPRAGE images from an in vivo data set. (a) shows the ground truth (from
fully sampled data) and the reconstructed image from sparsely sampled data
using DL and the proposed method with a factor of 5 acceleration; (b) and (c)
show the corresponding segmented tissue images and the residual images. As seen
from the segmentation results, the MPRAGE reconstructions from the proposed
method preserved the tissue structures well.