0685
Unsupervised Image Reconstruction using Deep Generative Adversarial Networks1Electrical Engineering, Stanford University, Stanford, CA, United States, 2Radiology, Stanford University, Stanford, CA, United States
Synopsis
Many deep learning-based reconstruction methods require fully-sampled ground truth data for supervised training. However, instances exist where acquiring fully sampled data is either difficult or impossible, such as in dynamic contrast enhancement (DCE), 3D cardiac cine, 4D flow, etc. for training a reconstruction network. We present a deep learning framework for reconstructing MRI without using any fully sampled data. We test the method in two scenarios, and find the method produces higher quality images which reveal vessels and recover more anatomical structure. This method has potential in applications, such as DCE, cardiac cine, low contrast agent imaging, and real-time imaging.
Introduction
Many techniques exist for reconstruction in accelerated imaging, such as compressed sensing (CS)1, parallel imaging2, and various deep learning (DL) methods.3–6 Most of these DL techniques require fully-sampled ground truth data for training. This poses a problem for applications such as dynamic contrast enhancement (DCE), 4D flow, etc. where the collection of fully-sampled datasets is time-consuming, difficult, or impossible.There are three main ways to surmount this problem. First, CS can reconstruct the ground truth in the DL framework. However, the reconstructed images are unlikely to be better than CS images. The second way is to restrict DL reconstruction to applications with fully-sampled training datasets, excluding applications such as DCE or 4D flow. The third way is to formulate DL training to use only undersampled datasets.7–11
We describe a generative model for learned image reconstruction using only undersampled datasets and no fully-sampled datasets. This allows for DL reconstruction when it is impossible or difficult to obtain fully sampled data.
Methods
We have created a DL framework to reconstruct MR images using only undersampled datasets for training. The input to this network is an undersampled two-dimensional image and the output is a reconstructed two-dimensional image (Figure 1).Complex images from zero-filled reconstruction of undersampled data are input into the generator. This reconstruction network attempts to generate an image, Xg, of higher quality than the input. Next, a sensing matrix comprised of coil sensitivity maps generated using ESPIRiT,14 an FFT, an undersampling mask, and an IFFT is applied to Xg to generate measured image Yg. A different image from the same dataset of undersampled images acts as the real measured image Yr. Finally, the discriminator differentiates between generated and real measured images.15
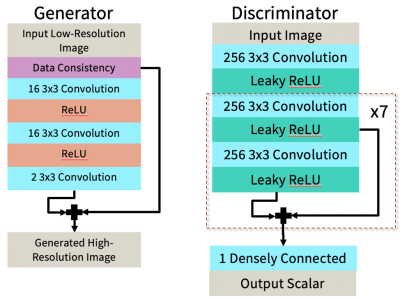
The loss functions of the generator and discriminator originate from the Wasserstein GAN with gradient penalty (WGAN-GP).16 Here, Dloss = D(fake measurement) – D(real measurement) + gradient penalty and Gloss = -D(fake measurement).
An unrolled network 3,17 based on the Iterative Shrinkage-Thresholding Algorithm (ISTA) 18 is used as the generator architecture (Figure 2a), and the discriminator is shown in Figure 2b.
We tested the framework in two scenarios. The first was fully sampled 3T knee images acquired using a 3D FSE CUBE sequence with proton density weighting including fat saturation.19 15 subjects were used for training; each subject had a complex-valued volume of size 320x320x256 that was split into axial slices. Because a fully-sampled ground truth exists for this scenario, we can quantitatively validate our results. We created undersampled images by applying pseudo-random Poisson-disc variable-density sampling masks to the fully-sampled k-space. Although we initially use fully-sampled datasets to create sub-sampled datasets, the generator and discriminator are never trained with fully-sampled data.
The second scenario consists of dynamic contrast enhanced (DCE) acquisitions of the abdomen, with a fat-suppressed butterfly-navigated free-breathing SPGR acquisition with an acceleration factor of 5. 886 subjects were used for training. Because DCE is inherently undersampled, we have no ground truth to assess performance. Instead, we compare to CS reconstruction and qualitatively evaluate the sharpness of the vessels and other anatomical structures in the generated images.
Results
Representative results in the knee scenario are shown in Figure 3 with an undersampling factor of 2 in both ky and kz. The generator markedly improves the image quality by recovering vessels and structures that were not visible before but uses no ground truth data in the training. Figure 4 displays a comparison between our results and CS with L1-wavelet regularization on our test dataset.Representative DCE results are shown in Figure 5. The generator improves the image quality by recovering sharpness and adding more structure to the input images.
Discussion
In the knee scenario, the generated images are quite similar to the ground truth. In the DCE application, the generated images are sharper than those reconstructed by CS and have higher diagnostic quality.The main advantage of this method over existing DL reconstruction methods is obviation of fully-sampled data. Additionally, the method produces better quality reconstruction compared to baseline CS methods.
While the method has been demonstrated here for reconstructing undersampled fast spin echo and DCE datasets, the discriminator can act on any simulated lossy measurement as long as the measurement process is known. Therefore, this method could also be useful for high noise environments where the acquisition of high SNR data is difficult. Other adverse situations where ground truth data are precluded include real-time imaging due to motion and arterial spin labeling due to low SNR. Further applications where it is hard to fully sample are time-resolved MR angiography, cardiac cine, low contrast agent imaging, EPI-based sequences, diffusion tensor imaging, and fMRI.
Conclusion
Our method has applications in cases where fully-sampled datasets are difficult to obtain or unavailable. We will continue refining the quality of the framework as applied to these scenarios and other applications.Acknowledgements
We would like to acknowledge support from GE Healthcare and the National Institute of Health, specifically grants NIH R01 EB009690 and NIH R01 EB026136.References
1. Lustig M, Donoho D, Pauly JM. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn Reson Med. 2007;58(6):1182-1195. doi:10.1002/mrm.21391
2. Murphy M, Alley M, Demmel J, Keutzer K, Vasanawala S, Lustig M. Fast ℓ 1-SPIRiT compressed sensing parallel imaging MRI: Scalable parallel implementation and clinically feasible runtime. IEEE Trans Med Imaging. 2012;31(6):1250-1262. doi:10.1109/TMI.2012.2188039
3. Cheng JY, Chen F, Alley MT, Pauly JM, Vasanawala SS. Highly Scalable Image Reconstruction using Deep Neural Networks with Bandpass Filtering. May 2018. http://arxiv.org/abs/1805.03300.
4. Hammernik K, Klatzer T, Kobler E, et al. Learning a variational network for reconstruction of accelerated MRI data. Magn Reson Med. 2018;79(6):3055-3071. doi:10.1002/mrm.26977
5. Mardani M, Gong E, Cheng JY, et al. Deep Generative Adversarial Networks for Compressed Sensing Automates MRI. May 2017. http://arxiv.org/abs/1706.00051.
6. Yang G, Yu S, Dong H, et al. DAGAN: Deep De-Aliasing Generative Adversarial Networks for Fast Compressed Sensing MRI Reconstruction. IEEE Trans Med Imaging. 2018;37(6):1310-1321. doi:10.1109/TMI.2017.2785879
7. Tamir JI, Yu SX, Lustig M. Unsupervised Deep Basis Pursuit: Learning Inverse Problems without Ground-Truth Data.
8. Zhussip M, Soltanayev S, Chun SY. Training deep learning based image denoisers from undersampled measurements without ground truth and without image prior. June 2018. http://arxiv.org/abs/1806.00961. 9. Lehtinen J, Munkberg J, Hasselgren J, et al. Noise2Noise: Learning Image Restoration without Clean Data.; 2018. http://r0k.us/graphics/kodak/.
10. Soltanayev S, Chun Y. Training Deep Learning Based Denoisers without Ground Truth Data. https://github.com/Shakarim94/Net-SURE.
11. Lei K, Mardani M, Pauly JM, Vasawanala SS. Wasserstein GANs for MR Imaging: from Paired to Unpaired Training. October 2019. http://arxiv.org/abs/1910.07048.
12. Yaman B, Hosseini SAH, Moeller S, Ellermann J, Uǧurbil K, Akçakaya M. Self-Supervised Physics-Based Deep Learning MRI Reconstruction Without Fully-Sampled Data. October 2019. http://arxiv.org/abs/1910.09116.
13. Chen F, Cheng JY, Pauly JM, Vasanawala SS. Semi-Supervised Learning for Reconstructing Under-Sampled MR Scans. https://cds.ismrm.org/protected/19MPresentations/abstracts/4649.htmlhttps://cds.ismrm.org/protected/19MPresentations/abstracts/4649.html.
14. Uecker M, Lai P, Murphy MJ, et al. ESPIRiT - An eigenvalue approach to autocalibrating parallel MRI: Where SENSE meets GRAPPA. Magn Reson Med. 2014;71(3):990-1001. doi:10.1002/mrm.24751
15. Bora A, Price E, Dimakis AG. AmbientGAN: Generative models from lossy measurements. In: ICLR. 2018.
16. Gulrajani I, Ahmed F, Arjovsky M, Dumoulin V, Courville A. Improved Training of Wasserstein GANs. March 2017. http://arxiv.org/abs/1704.00028.
17. Diamond S, Sitzmann V, Heide F, Wetzstein G. Unrolled Optimization with Deep Priors. May 2017. http://arxiv.org/abs/1705.08041.
18. Beck A, Teboulle M. A Fast Iterative Shrinkage-Thresholding Algorithm for Linear Inverse Problems. SIAM J Imaging Sci. 2009;2(1):183-202. doi:10.1137/080716542
19. K. Epperson, A. M. Sawyer, M. Lustig, M. T. Alley, M. Uecker, P. Virtue, P. Lai A, Vasanawala SS. Creation of Fully Sampled MR Data Repository for Compressed Sensing of the Knee. In: SMRT 22nd Annual Meeting. Salt Lake City, Utah, USA; 2013.
Figures