0681

Artificial neural networks for numerical differentiation with application to magnetic resonance elastography

Matthew C Murphy¹, Joshua D Trzasko¹, Jonathan M Scott¹, Armando Manduca¹, John Huston, III¹, and Richard L Ehman¹
¹Mayo Clinic, Rochester, MN, United States

Synopsis

An artificial neural network (ANN) was trained to estimate the partial derivatives of a spatially varying field, and compared against a finite difference approach. For the application of elastography, training data were generated using a wave equation. After the training examples were corrupted by noise and missing data, the network was trained to estimate the analytical solution to the partial derivatives. In simulation, the ANN improved accuracy in noisy data but blurred sharp boundaries relative to a finite difference method. In vivo, using the ANN to compute the curl of the displacement field improved confidence in subsequent property estimates.

Introduction

In imaging applications it is sometimes necessary to estimate the derivative of a spatially varying function given noisy, discretely sampled data. A common approach to this task is to compute finite differences, which are susceptible to discretization errors and amplify noise. These deficiencies may be overcome by conventional regularized estimation,¹ but the appropriate regularization transform, function, and weighting term must be chosen and evaluated for a given application. In this study, we hypothesized that a learning-based approach could improve the accuracy of numerical differentiation compared to a finite difference approach, and that the appropriate regularization could be achieved by selection of the forward model used to generate training data. Though several potential applications exist, here we evaluated this approach in the context of magnetic resonance elastography (MRE), specifically for the computation of the curl of the displacement field. This computation is often performed before inversion to remove the effects of longitudinal waves on the estimated mechanical properties.

Methods

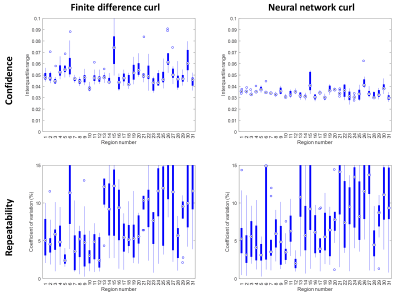
Training data were generated using analytical functions and then corrupted by noise and missing data to mimic measured displacement fields. Given the MRE application, we chose the equation of a wave traveling through a homogeneous viscoelastic material to generate the training data, u(r) = r^-1e^-αrsin(kr – φ₀), where u is the displacement, r is distance from the wave source, α is the attenuation coefficient, k is the wave number, and φ₀ is the initial phase. To generate a training example, this equation and the analytical solutions to its partial derivatives were evaluated on a 7×7×7 grid with 3-mm isotropic spacing to match the acquired MRE data. Up to 5 wave sources were placed at random locations outside the patch with randomly assigned φ₀, as well as parameters k and α, which were chosen randomly from a range commonly observed in vivo. Zero-mean Gaussian noise was added to each example with a randomly selected signal-to-noise ratio in the range of 1 to 50. Finally, to improve curl estimates at edges, a randomly selected mask patch taken from in vivo data was applied to each training example. Each example was scaled from -1 to 1. We then trained an Inception-like neural network² using the Keras API³ with a TensorFlow backend⁴ to estimate the three partial spatial derivatives at the central voxel of the patch given the noisy, masked simulated displacements. The network was fit to minimize mean absolute error (MAE) using an Adam optimizer⁵ with a mini-batch size of 100 examples and 1000 mini-batches per epoch. Mini-batches of training data were generated in real time until the stopping criterion was reached. Network fitting was performed at 3 learning rates (0.001, 0.0003, and 0.0001), each time stopping when the MAE was not improved for 3 consecutive epochs.

The trained network was evaluated in a test set and a coupled-harmonic oscillator (CHO) simulation,6 and compared against a finite difference approach in both cases. Finally, we used previously acquired brain MRE data (10 subjects with 3 repeat scans) to assess confidence and repeatability of mechanical property estimates.⁷ Mechanical property maps were computed using an edge-aware neural network inversion,⁸ and error maps were computed as the interquartile range (IQR) of the prediction interval using quantile regression. For each exam, mean mechanical property values and corresponding IQR were computed in 31 regions using a modified AAL atlas excluding regions with <10 voxels. From these summary data, the mean IQR across trials was computed to assess confidence and the coefficient of variation was computed to assess repeatability.

Results

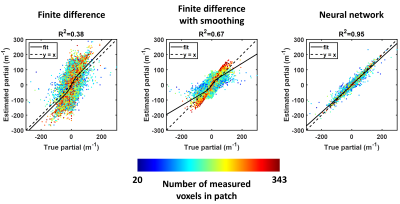
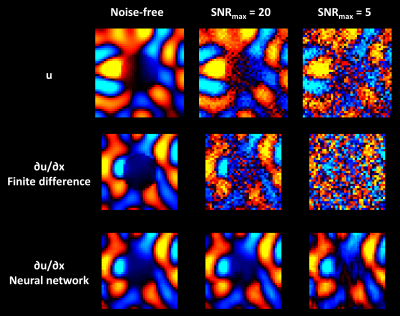
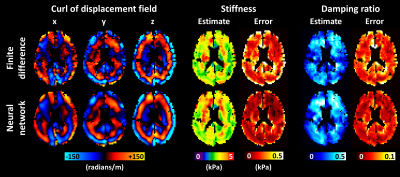
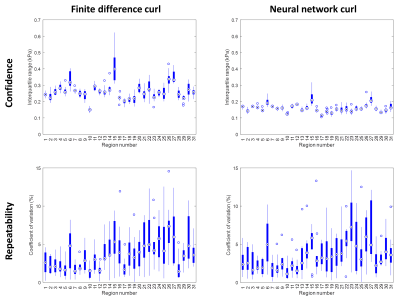
Figure 1 shows test set results. Since the neural network had a larger spatial footprint, we tested varying degrees of pre-smoothing the data before computing finite differences and included the most accurate result in Figure 1. The neural network estimate was more accurate and less biased by missing data than the finite difference approach both without and with pre-smoothing. A CHO-simulated displacement field with a sharp transition in material properties is shown in Figure 2. The neural network-based estimate of ∂u/∂x is more resistant to noise but blurs the boundary compared to the finite difference method. An in vivo example (Fig. 3) shows reduced estimated errors in the mechanical property maps when using the neural network to compute the curl. The summary of confidence and repeatability in the stiffness measurements is shown in Figure 4, indicating significantly improved confidence using the trained network to compute the curl (39% decrease in mean IQR, difference in IQR tested using mixed-effects model, P<0.001), though no significant difference in repeatability was observed. Summarizing the results of damping ratio (Fig. 5), we again observed significantly improved confidence (31% decrease in mean IQR, P<0.001) but no difference in repeatability.

Discussion and conclusion

In this study, we demonstrated the feasibility of training an artificial neural network to perform numerical differentiation of noisy, discrete data for the application of MR elastography. In simulation, the trained network improved accuracy, particularly in noisy data, though it did blur sharp transitions in the displacement field. In vivo, we evaluated this approach for computing the curl of the displacement field prior to inversion and observed no significant change in repeatability but confidence in the property estimates was significantly improved.

Acknowledgements

No acknowledgement found.

References

1. Chartrand R. Numerical Differentiation of Noisy, Nonsmooth Data. ISRN Applied Mathematics. 2011;2011:11. doi: 10.5402/2011/164564.

2. Szegedy C, Ioffe S, Vanhoucke V, Alemi AA, editors. Inception-v4, inception-resnet and the impact of residual connections on learning. Thirty-First AAAI Conference on Artificial Intelligence; 2017.

3. Chollet F. Keras (2015). 2017.

4. Abadi M, Agarwal A, Barham P, Brevdo E, Chen Z, Citro C, Corrado GS, Davis A, Dean J, Devin M, Ghemawat S, Goodfellow I, Harp A, Irving G, Isard M, Jozefowicz R, Jia Y, Kaiser L, Kudlur M, Levenberg J, Mané D, Schuster M, Monga R, Moore S, Murray D, Olah C, Shlens J, Steiner B, Sutskever I, Talwar K, Tucker P, Vanhoucke V, Vasudevan V, Viégas F, Vinyals O, Warden P, Wattenberg M, Wicke M, Yu Y, Zheng X, editors. Tensorflow: A system for large-scale machine learning. Software available from tensorfloworg; 2015.

5. Kingma DP, Ba J. Adam: A method for stochastic optimization. arXiv preprint arXiv:14126980. 2014.

6. Braun J, Buntkowsky G, Bernarding J, Tolxdorff T, Sack I. Simulation and analysis of magnetic resonance elastography wave images using coupled harmonic oscillators and Gaussian local frequency estimation. Magn Reson Imaging. 2001;19(5):703-13. doi: Doi 10.1016/S0730-725x(01)00387-3. PubMed PMID: WOS:000170371500013.

7. Murphy MC, Huston J, 3rd, Jack CR, Jr., Glaser KJ, Senjem ML, Chen J, Manduca A, Felmlee JP, Ehman RL. Measuring the characteristic topography of brain stiffness with magnetic resonance elastography. PloS one. 2013;8(12):e81668. doi: 10.1371/journal.pone.0081668. PubMed PMID: 24312570; PMCID: 3847077.

8. Murphy MC, Manduca A, Trzasko JD, Glaser KJ, Huston J, 3rd, Ehman RL. Artificial neural networks for stiffness estimation in magnetic resonance elastography. Magnetic resonance in medicine. 2018;80(1):351-60. doi: 10.1002/mrm.27019. PubMed PMID: 29193306; PMCID: 5876084.

Figures

Summary of test set results using 3 methods to compute the partial derivatives. Each point in the scatter plot represents a partial of the simulated data patch (i.e., three points in each plot per example). The color of each point signifies the number of non-zero voxels in the randomly selected mask patch used to impose missing data.

Results in a displacement field simulated by coupled-harmonic oscillators with increasing levels of noise added. The simulated material was assigned a stiff, circular inclusion to assess performance at sharp boundaries in the displacement field. The neural network blurs the boundary but is more accurate in noisy regions.

Example in vivo images. In the top row are the three components of the curl of the displacement field computed using finite differences, along with the subsequent estimates of stiffness and damping ratio. Each of the mechanical property maps is accompanied by an error map, which was computed as the difference between the 75th and 25th percentiles of the prediction interval using quantile regression. Analogous results using the trained network to compute the curl are shown in the bottom row.

Summary of in vivo stiffness measurements with each box plot displaying the distribution over the 10 participants. Confidence in the stiffness estimates (computed as interquartile range of stiffness estimate by quantile regression) was significantly improved using the neural network version of the curl. Repeatability was not statistically different between the two methods.

Summary of in vivo damping ratio measurements with each box plot displaying the distribution over the 10 participants. Confidence in the damping ratio estimates (computed as interquartile range of stiffness estimate by quantile regression) was significantly improved using the neural network version of the curl. Repeatability was not statistically different between the two methods.

Proc. Intl. Soc. Mag. Reson. Med. 28 (2020)

0681