Introduction

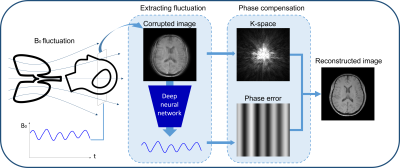
Respiration-induced B₀ fluctuation can produce substantial artifacts in the brain images^1,2. A popular approach to reduce the artifacts is to use a navigator echo³. However, it requires a modification in a sequence. Recently, deep learning-based artifact correction methods have been proposed⁴ to generate artifact-free images. However, most of these methods utilized end-to-end training and, therefore, the function of the network is not clearly defined. Furthermore, the methods may be susceptible to unexpected artifact creation. In this study, we designed a deep neural network, DeepRespi, to extract a respiration pattern from an artifact-corrupted image. Then, the pattern was utilized to compensate for the respiration-induced phase error, generating an artifact-corrected image (Figure 1).

Methods

[Datasets]
To train and evaluate DeepRespi, complex-valued GRE images of 23 subjects (11 healthy controls (HC) and 12 patients with hemorrhage) were utilized. The dataset was acquired with three different scan protocols: 8 HC with FOV = 224x224x176 mm³, voxel size = 1 mm³, TR = 33 ms, TE = 25 ms; 3 HC with FOV = 176x176x100 mm³, voxel size = 1 mm³, TR = 33 ms, TE = 25 ms; and 11 patients with FOV = 220x220x144 mm³, voxel size = 0.5x0.5x2 mm³, TR = 36 ms, TE = 25 ms. These data were resized to 224x224. Then, low SNR images were discarded, resulting in a total of 1890 2D complex images. Out of these images, 1465 images were utilized for training and 425 images were utilized for evaluation. None of these images had artifacts. For respiration patterns, respiration recording data of 111 subjects, each with 2730 seconds were utilized. The data were bandpass-filtered between 0.1 Hz and 1 Hz and normalized.

[Generation of respiration artifact-corrupted images]
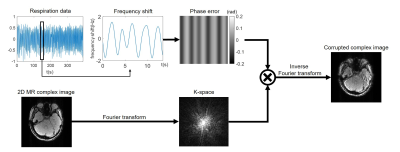
Using the GRE images and respiration patterns, respiration artifact-corrupted images were generated (Figure 2). The respiration pattern was scaled to have a maximum frequency shift between 1 Hz and 2 Hz⁵. This frequency shift was translated into 2D phase error, assuming a sequential encoding in 2D Cartesian readout with TR of 60 ms. Then, a corrupted image was generated as summarized in Fig. 2. By randomly combining the GRE images and respiration patterns, one million 2D corrupted images were generated for training and 10,000 for evaluation.

[Convolution neural network: DeepRespi]
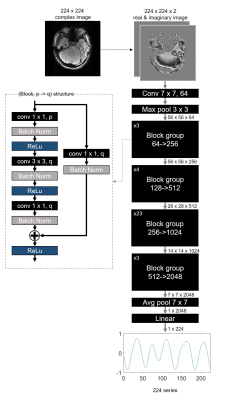
DeepRespi was designed to extract a respiration pattern from a corrupted complex image (Figure 3). The network was trained by the one million corrupted images and the corresponding respiration patterns. ResNet101⁶ was used as the network structure. For the input of the network, the real and imaginary parts of the complex image were used. L2 loss, ADAM optimizer with a learning rate of 0.002 and L2 regularizer were utilized.

[Respiration correction]
The output of DeepRespi, which is a respiration pattern, was reformatted into 2D phase error in the same way as in the generation. Then, this error was corrected by negating the phase and applying it into the k-space of the corrupted image. Finally, a respiration-corrected image was generated.

[Evaluation]
Total 10,000 corrupted images that were not included in the training set were utilized for the evaluation. After the respiration pattern estimation and correction, the respiration corrected-images were evaluated by normalized-root-mean-squared error (NRMSE) and structural similarity (SSIM) with the uncorrupted images as the reference. The histograms of NRMSE and SSIM were plotted for the corrupted and corrected images. Additionally, a correlation coefficient between the input respiration pattern and the DeepRespi-generated respiration pattern was calculated.

Results

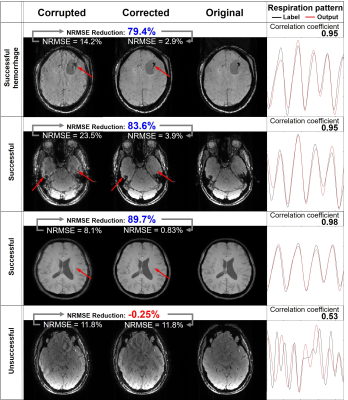
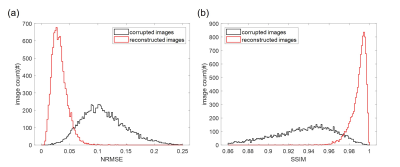
Figure 4 shows the corrupted images, corrected images, original images and input and DeepRespi-generated respiration patterns of four examples (three successful and one unsuccessful example). The successful examples show clear improvements in image quality even for the hemorrhage patient (see red arrows indicating artifacts). However, not all images were successful as shown in the last row. Still, increased NRMSE after the correction was very rare (only 45 images out of 10000 images). Overall, NRMSE was reduced from 11.0 ± 3.9% (corrupted images) to 3.2 ± 1.4% (corrected images), showing 68.9 ± 13.2% reduction. SSIM was increased from 0.93 ± 0.03 (corrupted images) to 0.99 ± 0.01 (corrected images), reporting improvement after the correction. As summarized in the histograms of NRMSE (Figure 5), most images (89.6%) resulted in NRMSE less than 5% after applying our method. The DeepRespi-extracted respiration patterns showed a high correlation with the input respiration patterns (correlation coefficient of 0.94 ± 0.04).

Discussion and Conclusion

In this study, we proposed a deep neural network, DeepRespi, that extracts a respiration pattern from a corrupted complex GRE image. The results show successful compensation of the respiration-induced B₀ artifacts for simulated data. Further tests with respiration-corrupted in-vivo data are warranted. As compared to other deep learning methods, the function of our method is well-defined, and, therefore, the worry of deep learning as a black box is less problematic.